numpy
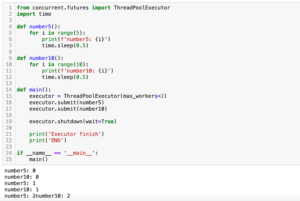
前回、並列処理concurrent.futuresのThreadPoolExecutorで複数の処理を実行した際、他の処理を待つ方法を紹介しました。
今回はnumpyで三角関数を扱う方法を解説していきます。
三角関数は高校の数学でもやったかと思いますが、三角形の辺の長さと角度を相互に計算する関数です。
0°から180°までの代表的な値はこんな感じでした。
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | |
| sin | 0 | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 |
| cos | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 | \(-\frac{1}{2}\) | \(-\frac{1}{\sqrt{2}}\) | \(-\frac{\sqrt{3}}{2}\) | -1 |
| tan | 0 | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | なし | \(-\sqrt{3}\) | -1 | \(-\frac{1}{\sqrt{3}}\) | 0 |
ちなみに\(\frac{1}{\sqrt{2}}\)は0.70711、\(\frac{\sqrt{3}}{2}\)は0.86603、\(\frac{1}{\sqrt{3}}\)は0.57735、\(\sqrt{3}\)は1.73205です。
それでは始めていきましょう。
ラジアン
まず重要なこととして、numpyの三角関数では角度の値として度(°)ではなくラジアンを使います。
角度からラジアンへの変換は角度に\(\pi/180\)をかけます。
毎回上記の計算式を書いてもいいですが、numpyでの度からラジアンへの変換は「np.radians(度)」で行うと楽です。
import numpy as np
angle = 30
angle_radian = np.radians(angle)
print(angle)
print(angle_radian)
実行結果
30
0.5235987755982988三角関数の計算(一つの角度)
numpyで三角関数を一つの角度に対して行う場合は「np.sin(角度)」、「np.cos(角度)」、「np.tan(角度)」です。
import numpy as np
angle = 30
angle_radian = np.radians(angle)
print(np.sin(angle_radian))
print(np.cos(angle_radian))
print(np.tan(angle_radian))
実行結果
0.49999999999999994
0.8660254037844387
0.5773502691896256それぞれ正しい値が計算されているのが分かります。
ちなみに度とラジアンの両方でsinの計算をしてみるとこんな感じになります。
import numpy as np
angle = 30
angle_radian = np.radians(angle)
print(np.sin(angle))
print(np.sin(angle_radian))
実行結果
-0.9880316240928618
0.49999999999999994度で計算した方が値が間違っています。
ということで角度をラジアンに変換することを忘れないようにしましょう。
三角関数の計算(複数の角度)
numpyを使った三角関数の計算ではリストを使って複数の角度を一度に計算することも可能です。
またその時も先ほどの一つの角度の計算のコマンドと同じで「np.sin(角度のリスト)」、「np.cos(角度のリスト)」、「np.tan(角度のリスト)」です。
import numpy as np
angles_degree = [0, 30, 45, 60, 90]
angles_radian = np.radians(angles_degree)
print(np.sin(angles_radian))
print(np.cos(angles_radian))
print(np.tan(angles_radian))
実行結果
[0. 0.5 0.70710678 0.8660254 1. ]
[1.00000000e+00 8.66025404e-01 7.07106781e-01 5.00000000e-01
6.12323400e-17]
[0.00000000e+00 5.77350269e-01 1.00000000e+00 1.73205081e+00
1.63312394e+16]逆三角関数
sin、cos、tanの値から角度を求める関数を「逆三角関数」と言いますが、numpyでは逆三角関数も計算することができます。
その場合は「np.arcsin(角度)」、「np.arccos(角度)」、「np.arctan(角度)」を使います。
import numpy as np
angles_degree = [0, 30, 45, 60, 90]
angles_radian = np.radians(angles_degree)
sin_val = np.sin(angles_radian)
cos_val = np.cos(angles_radian)
tan_val = np.tan(angles_radian)
print(np.arcsin(sin_val))
print(np.arccos(cos_val))
print(np.arctan(tan_val))
実行結果
[0. 0.52359878 0.78539816 1.04719755 1.57079633]
[0. 0.52359878 0.78539816 1.04719755 1.57079633]
[0. 0.52359878 0.78539816 1.04719755 1.57079633]ラジアンから度への変換
ラジアンから度への変換をするには「np.degrees(ラジアン)」を用います。
import numpy as np
angles_degree = [0, 30, 45, 60, 90]
angles_radian = np.radians(angles_degree)
print(np.degrees(angles_radian))
実行結果
[ 0. 30. 45. 60. 90.]おまけ:sin、cosのプロット
最後におまけとしてmatplotlibを使ってsinとcosの波をプロットしてみましょう。
import numpy as np
import matplotlib.pyplot as plt
angle_list = range(0,1080)
radian_list = np.radians(angle_list)
sin_list = np.sin(radian_list)
cos_list = np.cos(radian_list)
fig = plt.figure()
plt.clf()
plt.plot(angle_list, sin_list)
plt.plot(angle_list, cos_list)
plt.show()
実行結果
「angle_list = range(0,1080)」で0°から1079°までの角度のリストを作り、「radian_list = np.radians(angle_list)」でラジアンのリストに変換しています。
そして「sin_list = np.sin(radian_list)」と「cos_list = np.cos(radian_list)」でsinとcosのリストに変換し、その後はmatplotlibでグラフ表示しています。
なぜこのタイミングで三角関数をやったかと言うと、実はPythonを使って音を出す際に三角関数が必要だったため勉強してみたということです。
ということで次回は三角関数を使ってPythonで音を出す、保存する方法を紹介します。
ではでは今回はこんな感じで。

コメント