Turtle
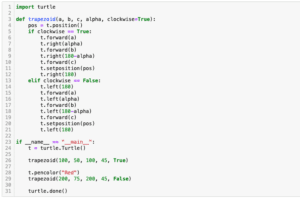
前回、PythonのグラフィックスライブラリTurtleで菱形、台形(平行四辺形)、星型、葉っぱ型の描き方を紹介しました。
今回は「再帰」と言われる処理を使って木を描いていきます。
それでは始めていきましょう。
再帰
Wikipediaによると「再帰」というのはこう定義されているようです。
ある物事について記述する際に、記述しているもの自体への参照が、その記述中にあらわれること
https://ja.wikipedia.org/wiki/再帰
プログラムでいうと、「プログラム中にそのプログラム自身を呼び出す記述があるプログラム」のようです。
理解するために単純なプログラムを用意してみました。
import turtle
def recursion(n, length, angle, times):
if n == 0:
return
t.forward(length)
t.right(angle)
next_length = length * times
recursion(n-1, next_length, angle, times)
if __name__ == "__main__":
t = turtle.Turtle()
recursion(10, 250, 75, 0.8)
turtle.done()このプログラムでは「recursion」という関数が定義されています。
そして「if __name__ == “__main__”:」以下の部分を見ていくと、turtleを呼び出し、recursionを実行しています。
recursion関数を見てみると、いきなり「if n == 0:」という記述がありますが、とりあえずここは飛ばします。
「t.forward(length)」で前に進み、「t.right(angle)」で右回りに回転しています。
その後、「next_length = length * times」で長さを変え、再度recursion関数を呼び出しています。
気をつけるべきことはここで呼び出されているrecursion関数の引数は「n-1, next_length, angle ,times」となっていることです。
数字を入れて見ていきましょう。
まず最初にrecursion関数を呼び出す際には引数は「10, 250, 75, 0.5」となっています。
そしてrecursion関数内でrecursion関数を呼び出す際(2回目)には、「n-1」と「next_length = length * times」により、「9, 125, 75, 0.5」となります。
また呼び出されたrecursion関数内でrecursion関数が呼び出され(3回目)、その際の引数は「8, 62.5, 75, 0.5」となります。
こうして何度も呼び出されているうちに「n-1 = 0」となる場面が出てきます。
その場合には先ほど解説を飛ばした「if n == 0:」の条件分岐に引っかかり、returnでこの関数は終了します。
こんな感じで自分で自分を呼び出す処理を「再帰処理」といいます。
ちなみに先ほどのプログラムではこんな感じの図形が描けます。
再帰処理で2分木を作成
ということで再帰処理を使って、枝が2本に分岐する木「2分木」を描くプログラムを作成してみました。
import turtle
def tree(n, length, angle, times_left, times_right):
if n == 0:
return
t.forward(length)
t.right(angle / 2)
length_right = length * times_right
tree(n-1, length_right, angle, times_left, times_right)
t.left(angle)
length_left = length * times_left
tree(n-1, length_left, angle, times_left, times_right)
t.right(angle/2)
t.backward(length)
if __name__ == "__main__":
t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(150)
t.pendown()
tree(5, 150, 60, 0.8, 0.7)
turtle.done()今回は関数treeを解説していきます。
まず「t.forward(length)」で前に進み、「t.right(angle / 2)」で右側の枝を描くために方向転換しています。
そして次の枝の長さを「length_right = length * times_right」で計算しています。
次が再帰処理になり「tree(n-1, length_right, angle, times_left, times_right)」で次の枝の処理へと進みます。
次の処理でも前に進み、右側の枝を描くために方向転換し、さらに次の枝の長さを計算し、次の再帰処理へと移ります。
こうしてまずは全ての分岐において右側の枝となる枝が描かれます。
そして「n=0」となった場合は、左の枝を描く処理に移り、まずは「t.left(angle)」で左の枝を描くために方向転換します。
ただし「n=0」の場合は左側の枝を描く処理「tree(n-1, length_left, angle, times_left, times_right)」もすぐにreturnで返されるため、そのまま下の処理に移ります。
「t.right(angle/2)」で一つ前の処理で移動してきた方向に向き直り、「t.backward(length)」で戻っています。
そしてn=1、n=2…というように逆回りにしながら左の枝を描きつつ、左に分岐した枝の右の枝を描いていくことになります。
なかなか文章だけでは分かりにくいので、プログラムを実行したこの動画を合わせて見てもらえると分かりやすいかと思います。
複数の枝を持つ木を描く方法
先ほどの例では2つの枝をもつ「2分木」でしたが、もっと多くの枝をもつ木を描くプログラムを作成してみました。
2分木の場合はまず右に指定した角度の半分の角度で回転し枝を描いたのち、左に行く場合は指定した角度を回転することで、初期の角度からいうと指定した角度の半分の角度左に向いている枝を描いていました。
複数の分岐をもつ場合は、2分木の場合と同じく、右に指定した角度の半分の角度で枝を描きますが、左に回転する場合は「指定した角度/枝の本数-1」で回転させます。
ということでこんな感じです。
import turtle
times_list = [0.8, 0.6, 0.4, 0.5]
def tree(n, length, angle, times_list):
if n == 0:
return
t.forward(length)
for i, times in enumerate(times_list):
if i == 0:
t.right(angle/2)
else:
t.left(angle/(len(times_list)-1))
next_length = length * times
tree(n-1, next_length, angle, times_list)
t.right(angle/2)
t.backward(length)
if __name__ == "__main__":
t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(150)
t.pendown()
tree(4, 150, 60, times_list)
turtle.done()次回は円と塗りつぶしを使って綺麗な図形を描いてみましょう。

ではでは今回はこんな感じで。

コメント