NumPy
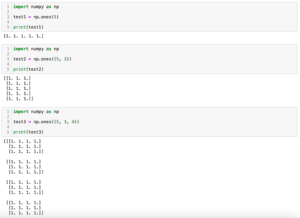
前回、PythonのNumPyで全ての要素が1の配列を作成する方法を紹介しました。
今回は逆フーリエ変換をして不要な周波数成分を除去する方法、すなわちローパスフィルタやハイパスフィルタ、バンドパスフィルタをPythonで行う方法を紹介します。
それでは始めていきましょう。
ランダムな合成波を作成
まずは多数のsin波を作成し、重ね合わせることでランダムな合成波を作成するプログラムを作成します。
ランダムな波形を作成する方法は、こちらの記事のプログラムを基本にしていますが、今回使いやすいように改変しています。

波の作成から表示まではこんな感じです。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
main_hz = 50
noise_hz_range = np.arange(0, 100, 1)
noise_level_max = 0.25
noise_hz_weight = [random.uniform(0, noise_level_max) for _ in noise_hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
data_list.append(np.sin(2*np.pi*main_hz*data_list[0] + random.random() * 2*np.pi))
for hz, w in zip(noise_hz_range, noise_hz_weight):
data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + random.random() * 2*np.pi))
columnnames = [hz for hz in noise_hz_range]
columnnames.insert(0, "Time")
columnnames.insert(1, "Main wave")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()使用するライブラリは「matplotlib」、「NumPy」、「Pandas」、「random」です。
変数「time」は波を作成する時間、変数「samplingrate」はサンプリングレートで、これらから一つの波で何データポイント作成するか決めます。
今回、メインとなる波を一つとそのメインの波を隠すようなノイズの波を作成します。
そこで変数「main_hz」はメインとなる波の周波数です。
またノイズの波の周波数は一つでは足りないので、変数「noise_hz_range」 にリスト形式で格納するようにしています。
ここでは「np.arange()」を使って、特定の範囲のリストを作成しています。
変数「noise_level_max」はメインの波の高さに対してのノイズの高さの割合の最大値です。
ここでは「0.25」としていますので、メインの波の高さの最大25%までのノイズが生まれる可能性が出ます。
それを変数「noise_hz_range」にある周波数分だけ割合をランダムに決めて格納しているのが、変数「noise_hz_weight」です。
次に実際にデータを作成していきます。
まず時間のデータをリスト内包表記で作成し、変数「data_list」に格納します。
data_list = [np.arange(0, time, 1/samplingrate)]メインの波を作成し、変数「data_list」に格納します。
ここでは「random.random() * 2*np.pi」を最後に足すことで、ランダムに位相をずらしています。
data_list.append(np.sin(2*np.pi*main_hz*data_list[0] + random.random() * 2*np.pi))ノイズにおける各周波数の波を作成し、変数「data_list」に格納します。
for hz, w in zip(noise_hz_range, noise_hz_weight):
data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + random.random() * 2*np.pi))ここまでできたら、Pandasのデータフレームにするために、各列の名前を変数「columnnames」にリスト形式で格納します。
columnnames = [hz for hz in noise_hz_range]
columnnames.insert(0, "Time")
columnnames.insert(1, "Main wave")そしてPandasのデータフレームにし、形を整えます。
ちなみに今回のように波をそれぞれ作成し、データフレームに格納すると行と列が逆になっているので「.transpose()」を使って行と列を入れ替え、その後、「.set_axis()」を使って列名を一括でセットしています。
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")最後に「.sum()」を使って、各列のデータをたし合わせます。
注意すべきは最初の列は時間なので足さない(df.iloc[:, 1:])ことです。
これ以降はmatplotlibでグラフを表示するための部分なので、解説は割愛します。
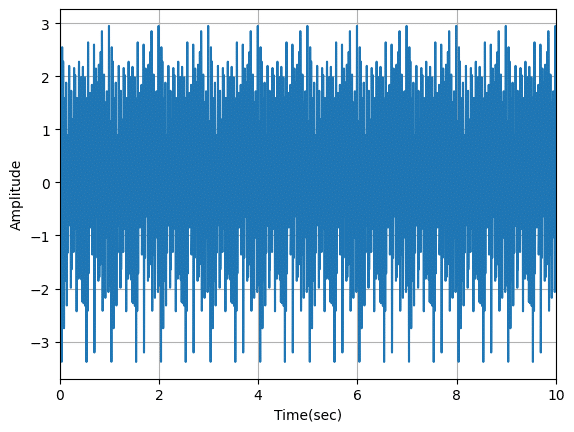
このプログラムを実行するとこんな感じで、ランダムな波形が得られます。
フーリエ変換
ローパスフィルタ、ハイパスフィルタ、バンドパスフィルタなど特定の周波数帯を除去するには、まずはフーリエ変換をして周波数解析を行う必要があります。
NumPyを使ったFFT(高速フーリエ変換)の方法はこちらの記事で解説していますので、よかったらどうぞ。
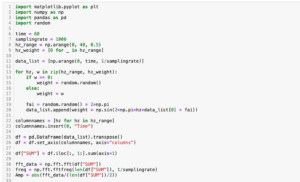
ということでここではプログラムだけお見せして、解説は割愛します。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
main_hz = 50
noise_hz_range = np.arange(0, 100, 1)
noise_level_max = 0.25
noise_hz_weight = [random.uniform(0, noise_level_max) for _ in noise_hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
data_list.append(np.sin(2*np.pi*main_hz*data_list[0] + random.random() * 2*np.pi))
for hz, w in zip(noise_hz_range, noise_hz_weight):
data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + random.random() * 2*np.pi))
columnnames = [hz for hz in noise_hz_range]
columnnames.insert(0, "Time")
columnnames.insert(1, "Main wave")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
#----------この部分を追加----------
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
#----------この部分を追加----------
#----------この部分は変更----------
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,100)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()
#----------この部分は変更----------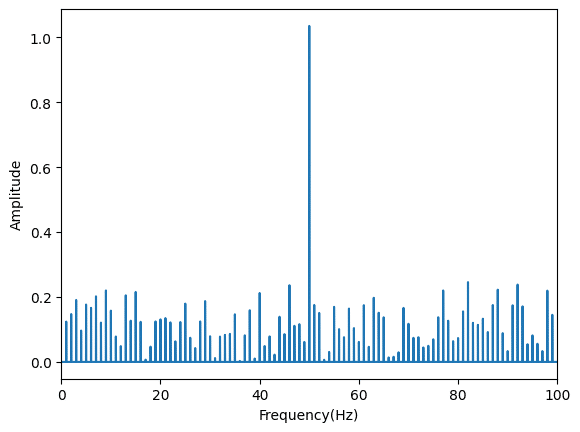
周波数解析の結果として、今回メインの波として指定した50 hzの強度が1となっており、他は0.25に抑えられています。
これで正しく波が作成され、正しく解析できていることが確認できました。
周波数をカットオフする方法
次に不要な周波数をカットオフします。
二つのNumPyのアレイ(配列)がある場合、例えば「array1」と「array2」とすると「array1[(array2 > 値)] = 0」とするとarray2で指定した値よりも大きい要素と同じインデックスのarray1の要素を0とすることができます。
つまり指定した値以下の部分はそのままなのでこれが「ローパスフィルタ」になります。
逆に「array1[(array2 < 値)] = 0」とするとarray2で指定した値よりも小さい要素と同じインデックスのarray1の要素を0とすることができます。
こちらは指定した値以上の部分はそのままなのでこれが「ハイパスフィルタ」になります。
そして両方指定すれば「バンドパスフィルタ」になるというわけです。
これを実装したプログラムがこちらです。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
main_hz = 50
noise_hz_range = np.arange(0, 100, 1)
noise_level_max = 0.25
noise_hz_weight = [random.uniform(0, noise_level_max) for _ in noise_hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
data_list.append(np.sin(2*np.pi*main_hz*data_list[0] + random.random() * 2*np.pi))
for hz, w in zip(noise_hz_range, noise_hz_weight):
data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + random.random() * 2*np.pi))
columnnames = [hz for hz in noise_hz_range]
columnnames.insert(0, "Time")
columnnames.insert(1, "Main wave")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
#----------この部分を追加----------
lowpass_cutoff = 60
highpass_cutoff = 40
fft_data_cutoff = fft_data.copy()
fft_data_cutoff[(freq > lowpass_cutoff)] = 0
fft_data_cutoff[(freq < highpass_cutoff)] = 0
Amp_cutoff = abs(fft_data_cutoff/(len(df["SUM"])/2))
#----------この部分を追加----------
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
#----------この部分を追加----------
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp_cutoff[1:int(len(df["SUM"])/2)])
#----------この部分を追加----------
plt.xlim(0,100)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()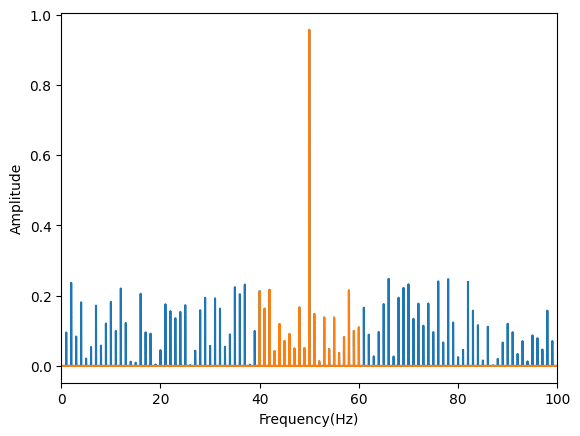
今回、ローパスフィルタのカットオフ周波数として60 Hzを、ハイパスフィルタのカットオフ周波数として40 Hzを指定しています。
橙色のグラフがカットオフ後のデータですが、ちゃんとカットオフされているのが分かります。
逆フーリエ変換
次に逆フーリエ変換をして周波数データから時系列データに戻します。
カットオフ後のデータ「fft_data_cutoff」を「np.fft.ifft()」を使って逆フーリエ変換を行い、そのデータに時間とサンプリングレートを掛けることで実際のデータに戻します。
ただし逆フーリエ変換後のデータは複素数になっていますが、実際に使うのは実部のみなので「np.real()」で実部のみ取得します。
ということでこんな感じ。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
main_hz = 50
noise_hz_range = np.arange(0, 100, 1)
noise_level_max = 0.25
noise_hz_weight = [random.uniform(0, noise_level_max) for _ in noise_hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
data_list.append(np.sin(2*np.pi*main_hz*data_list[0] + random.random() * 2*np.pi))
for hz, w in zip(noise_hz_range, noise_hz_weight):
data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + random.random() * 2*np.pi))
columnnames = [hz for hz in noise_hz_range]
columnnames.insert(0, "Time")
columnnames.insert(1, "Main wave")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
lowpass_cutoff = 60
highpass_cutoff = 40
fft_data_cutoff = fft_data.copy()
fft_data_cutoff[(freq > lowpass_cutoff)] = 0
fft_data_cutoff[(freq < highpass_cutoff)] = 0
Amp_cutoff = abs(fft_data_cutoff/(len(df["SUM"])/2))
#----------この部分を追加----------
data_cutoff = np.fft.ifft(fft_data_cutoff)
data_cutoff = np.real(data_cutoff*time*samplingrate)
#----------この部分を追加----------
#----------この部分は変更----------
fig = plt.figure()
plt.clf()
ax1 = fig.subplots()
ax2 = ax1.twinx()
ax1.plot(df["Time"], df["SUM"], color="tab:blue")
ax2.plot(df["Time"], data_cutoff, color="tab:orange")
plt.grid()
ax1.set_xlabel("Time(sec)")
ax1.set_ylabel("Amplitude")
ax2.set_ylabel("Amplitude(a.u.)")
ax1.set_xlim(0, 1)
plt.show()
#----------この部分は変更----------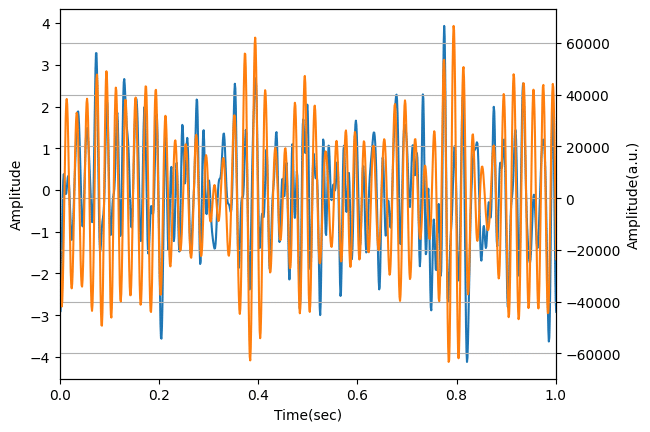
データが変わったのは分かりますが、本来欲しかった50 Hzの波だけにはなっていません。
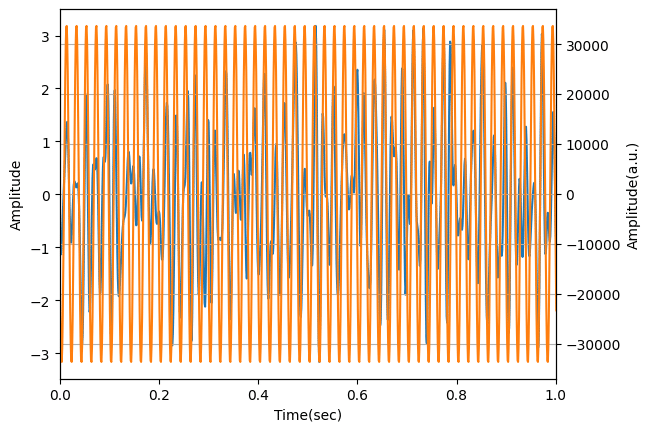
ちなみに「lowpass_cutoffを50.1」、「highpass_cutoffを49.9」にすると50 Hzの波が取得できます(当然と言えば当然ですが。。。)。
次回はNumPyで畳み込み積分と移動平均を計算する方法(np.convolve)を紹介します。
ではでは今回はこんな感じで。

コメント