NumPy
前回、PythonのNumPyを使って逆フーリエ変換をして不要な周波数成分を除去する方法(ローパスフィルタ、ハイパスフィルタ、バンドパスフィルタ)を紹介しました。
今回はNumPyで畳み込み積分と移動平均を計算する方法を紹介します。
畳み込み積分とは特定のグラフに対して、特定の範囲が移動しながら、たし合わせていく(つまり積分)計算になります。
またその特定の範囲においては、重み付けができ、特定の範囲内の値のどれを重視して足し合わせるかということができます。
ちなみに画像処理何かをやっているとたまに「コンボリューション(convolution)」なんて言葉が出てきますが、これを日本語にすると「畳み込み」となるそうです。
詳しくはWikipediaをご覧ください。
移動平均とはグラフデータである特定の点のデータを前後何点かのデータの平均ににする方法で、データのスムージングに用いられます。
この畳み込み積分と移動平均はNumPyの同じ関数「np.convolve()」で計算できるので、今回一緒に紹介します。
今回せっかくなので、畳み込み積分用にこんなデータを作ってみました。
import numpy as np
import matplotlib.pyplot as plt
import random
x_list = range(0, 100)
y_list = []
for i in x_list:
if i <= 10:
y_list.append(0)
elif i > 10 and i <= 30:
y_list.append(i-10)
elif i > 30 and i <= 50:
y_list.append(20)
elif i > 50 and i <= 70:
y_list.append(0)
elif i > 70 and i <= 90:
y_list.append(70-i)
elif i > 90:
y_list.append(0)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.show()
実行結果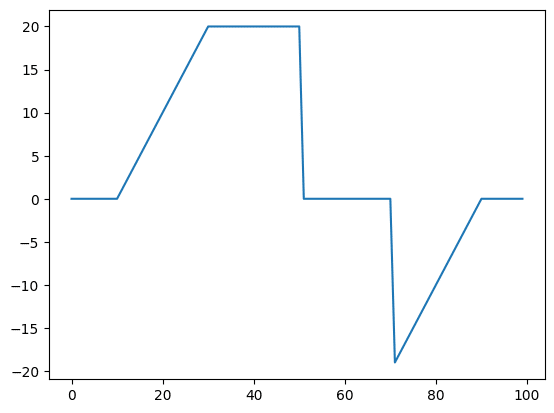
それでは始めていきましょう。
畳み込み積分
まずは畳み込み積分です。
先ほど作成したグラフに対して、移動してたし合わせていく範囲(重み情報込み)が必要になります。
その範囲のことを「窓関数」と言いますが、Pythonでは数値のリストで表現します。
例えば「[1, 1, 1, 1, 1]」とすると5点をそれぞれ1倍の値で足し合わせるということになります。
そしてNumPyの畳み込み関数「np.convolve()」は「np.convolve(グラフの数値のリスト, 窓関数のリスト, mode=”足し合せの範囲”)」とします。
modeに関しては次回解説を行いますが、個人的には「same」を使っておくのがいいのかと思っています。
ということでこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
import random
x_list = range(0, 100)
y_list = []
for i in x_list:
if i <= 10:
y_list.append(0)
elif i > 10 and i <= 30:
y_list.append(i-10)
elif i > 30 and i <= 50:
y_list.append(20)
elif i > 50 and i <= 70:
y_list.append(0)
elif i > 70 and i <= 90:
y_list.append(-20-(70-i))
elif i > 90:
y_list.append(0)
#----------この部分を追加----------
w = [1, 1, 1, 1, 1]
yma_list = np.convolve(y_list, w, mode="same")
#----------この部分を追加----------
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
#----------この部分を追加----------
plt.plot(x_list, yma_list)
#----------この部分を追加----------
plt.show()
実行結果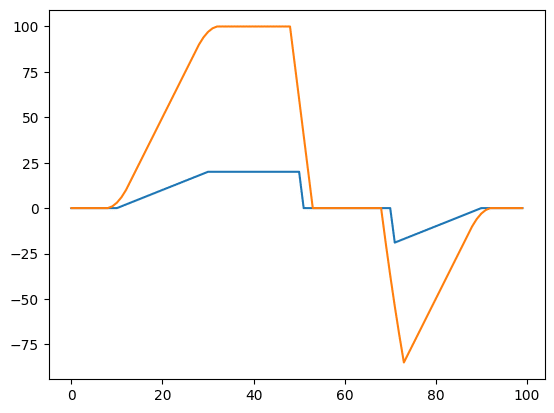
Xの値が30から50あたりを見ると、元のグラフでは20だったのですが、畳み込み積分をした後は100となっています。
窓関数を「1, 1, 1, 1, 1」と5つの点をそれぞれ1倍でたし合わせていることから「20 + 20 + 20 + 20 + 20 = 100」となったわけです。
窓関数を[0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.2, 0.1]に変えてみましょう。
import numpy as np
import matplotlib.pyplot as plt
import random
x_list = range(0, 100)
y_list = []
for i in x_list:
if i <= 10:
y_list.append(0)
elif i > 10 and i <= 30:
y_list.append(i-10)
elif i > 30 and i <= 50:
y_list.append(20)
elif i > 50 and i <= 70:
y_list.append(0)
elif i > 70 and i <= 90:
y_list.append(-20-(70-i))
elif i > 90:
y_list.append(0)
#----------この部分を変更----------
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.4, 0.3, 0.2, 0.1]
#----------この部分を変更----------
yma_list = np.convolve(y_list, w, mode="same")
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
実行結果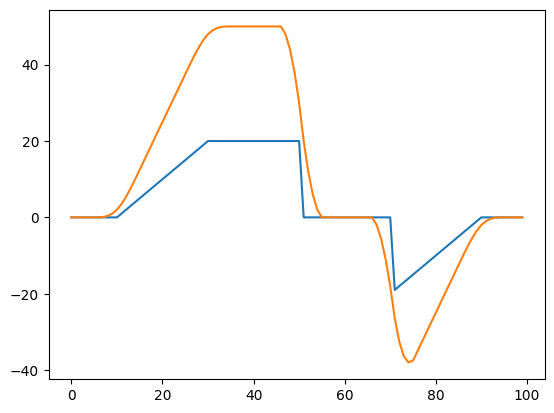
こんな感じで窓関数を変えると得られる結果は変わります。
移動平均
次に移動平均を計算してみましょう。
実は移動平均は畳み込み積分の中で窓関数がそれぞれ「1/窓関数の長さ」になっているものとなります。
つまり5個の点を使って移動平均を計算する場合は「1/5, 1/5, 1/5, 1/5, 1/5」という窓関数になるわけです。
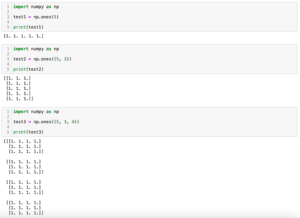
これをわざわざ数値で指定するのは面倒なので、まずは「np.ones()」で要素が1のリストを作り出し、その後、窓関数の長さで割り算してやることで窓関数を取得します。
ちなみに「np.ones()」はこちらの記事で紹介していますので、よかったらどうぞ。
ということでこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
import random
x_list = range(0, 100)
#----------この部分を追加----------
window = 5
#----------この部分を追加----------
y_list = []
for i in x_list:
if i <= 10:
y_list.append(0)
elif i > 10 and i <= 30:
y_list.append(i-10)
elif i > 30 and i <= 50:
y_list.append(20)
elif i > 50 and i <= 70:
y_list.append(0)
elif i > 70 and i <= 90:
y_list.append(-20-(70-i))
elif i > 90:
y_list.append(0)
#----------この部分を追加----------
w = np.ones(window)/window
#----------この部分を追加----------
yma_list = np.convolve(y_list, w, mode="same")
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
実行結果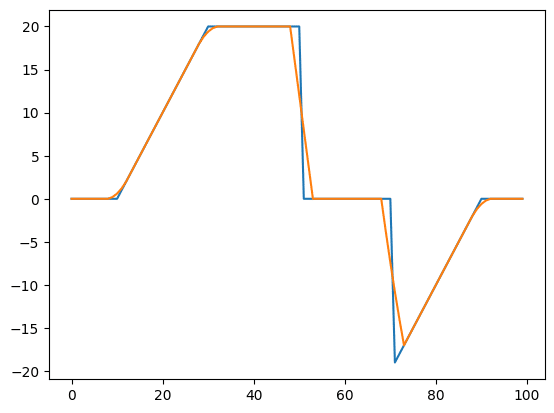
窓関数には色々とあるようなので、また機会があれば試してみたいものです。
次回はnp.convolveのmodeに関して比較してみます。
ではでは今回はこんな感じで。


コメント