lmfit
前回、Pythonのlmfitライブラリを使ったガウス関数、ローレンツ関数、フォークト関数の分布の表示とピークフィッティングの方法と結果の表示方法を紹介しました。
今回はlmfitライブラリを使って、複数のピークが混ざったグラフに対してピークフィッティングする方法を紹介します。
まずはピークフィッティングをするデータを、3つのガウス分布を足し合わせてこんな感じで作成してみました。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model = models.GaussianModel()
params = model.make_params()
output = model.fit(y_test, params, x=x_list)
fig = output.plot()
print(output.fit_report())
実行結果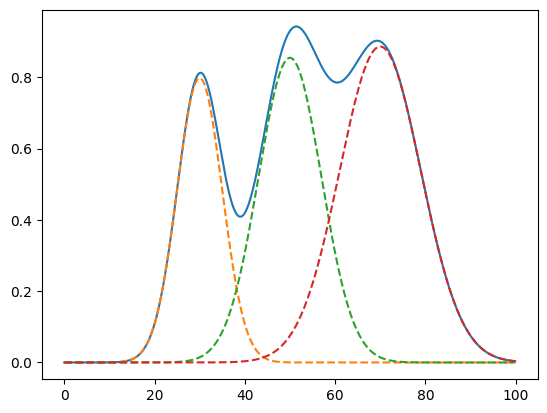
それでは始めていきましょう。
複数のピークに対してフィッティングする方法
まずは前回やった通り、1つのガウス関数をモデルとしてピークフィッティングをしてみましょう。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model = models.GaussianModel()
params = model.make_params()
output = model.fit(y_test, params, x=x_list)
fig = output.plot()
print(output.fit_report())
実行結果
[[Model]]
Model(gaussian)
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 9
# data points = 1000
# variables = 3
chi-square = 326.950203
reduced chi-square = 0.32793401
Akaike info crit = -1111.94740
Bayesian info crit = -1097.22414
R-squared = -1.62549494
[[Variables]]
amplitude: 2.1264e-06 +/- 2.52268867 (118636473.26%) (init = 1)
center: -0.93503795 +/- 1375080.01 (147061412.28%) (init = 0)
sigma: 1.86377649 +/- 927989.899 (49790836.11%) (init = 1)
fwhm: 4.38885810 +/- 2185249.18 (49790836.94%) == '2.3548200*sigma'
height: 4.5516e-07 +/- 0.33019431 (72545067.08%) == '0.3989423*amplitude/max(1e-15, sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(amplitude, center) = -0.9725
C(amplitude, sigma) = +0.9557
C(center, sigma) = -0.9295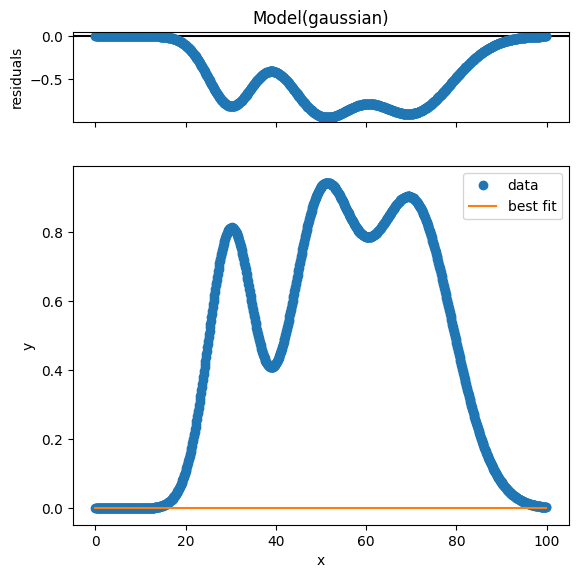
グラフの一致度を示すR-squared(1だと一致)を見ても、-1.62549494と全く相関が見られず、もちろんグラフを見ても全く一致していません。
つまり複数のピークがあるグラフに対して、1つのガウス関数では正しくフィッティングはできないというわけです。
ということで複数の関数が含まれたモデルを作成し、フィッティングします。
複数の関数が含まれたモデルを作成するのは簡単で、それぞれのモデルを足し合わせればいいだけです。
ただし1カ所注意する点は同じモデルを組み合わせる場合はそれぞれ別の名前をつける必要があります。
そのためモデルの引数に「prefix=”名前”」が必要になります。
今回の場合、ガウス関数のモデルを三つ使いますので、それぞれ「prefix=”gauss1_”」、「prefix=”gauss2_”」、「prefix=”gauss3_”」と名前をつけておきます。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.GaussianModel(prefix="gauss2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model.make_params()
output = model.fit(y_test, params, x=x_list)
fig = output.plot()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(gaussian, prefix='gauss2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 4054
# data points = 1000
# variables = 9
chi-square = 12.2530813
reduced chi-square = 0.01236436
Akaike info crit = -4383.97784
Bayesian info crit = -4339.80804
R-squared = 0.90160458
[[Variables]]
gauss1_amplitude: -179292.534 +/- 1.7249e+10 (9620532.86%) (init = 1)
gauss1_center: 49.5653927 +/- 343.743740 (693.52%) (init = 0)
gauss1_sigma: 17.9942836 +/- 3336.62719 (18542.71%) (init = 1)
gauss2_amplitude: -180962.322 +/- 1.7189e+10 (9498652.13%) (init = 1)
gauss2_center: 49.5837797 +/- 245.193463 (494.50%) (init = 0)
gauss2_sigma: 17.7889338 +/- 3226.36666 (18136.93%) (init = 1)
gauss3_amplitude: 360298.312 +/- 1.3536e+09 (375687.29%) (init = 1)
gauss3_center: 49.5753212 +/- 586.144788 (1182.33%) (init = 0)
gauss3_sigma: 17.8910754 +/- 6549.60193 (36608.21%) (init = 1)
gauss1_fwhm: 42.3732988 +/- 7857.15640 (18542.71%) == '2.3548200*gauss1_sigma'
gauss1_height: -3975.00549 +/- 3.8315e+08 (9639072.00%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_fwhm: 41.8897371 +/- 7597.51271 (18136.93%) == '2.3548200*gauss2_sigma'
gauss2_height: -4058.33907 +/- 3.8475e+08 (9480518.63%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_fwhm: 42.1302615 +/- 15423.1336 (36608.21%) == '2.3548200*gauss3_sigma'
gauss3_height: 8034.07489 +/- 30196195.6 (375851.56%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(gauss3_center, gauss3_sigma) = -1.0000
C(gauss1_center, gauss1_sigma) = -1.0000
C(gauss2_center, gauss2_sigma) = -0.9999
C(gauss1_amplitude, gauss1_center) = -0.9999
C(gauss2_amplitude, gauss2_sigma) = -0.9998
C(gauss1_amplitude, gauss1_sigma) = +0.9998
C(gauss2_amplitude, gauss2_center) = +0.9995
C(gauss1_amplitude, gauss3_center) = +0.9994
C(gauss1_amplitude, gauss3_sigma) = -0.9992
C(gauss2_amplitude, gauss3_sigma) = +0.9992
C(gauss2_amplitude, gauss3_center) = -0.9990
C(gauss1_center, gauss3_center) = -0.9989
C(gauss1_center, gauss3_sigma) = +0.9987
C(gauss1_sigma, gauss3_center) = +0.9985
C(gauss2_sigma, gauss3_sigma) = -0.9983
C(gauss1_sigma, gauss3_sigma) = -0.9983
C(gauss2_sigma, gauss3_center) = +0.9980
C(gauss2_center, gauss3_sigma) = +0.9976
C(gauss2_center, gauss3_center) = -0.9973
C(gauss1_amplitude, gauss2_amplitude) = -0.9969
C(gauss1_center, gauss2_amplitude) = +0.9959
C(gauss1_amplitude, gauss2_sigma) = +0.9952
C(gauss1_sigma, gauss2_amplitude) = -0.9952
C(gauss1_amplitude, gauss2_center) = -0.9941
C(gauss1_center, gauss2_sigma) = -0.9939
C(gauss1_sigma, gauss2_sigma) = +0.9931
C(gauss1_center, gauss2_center) = +0.9927
C(gauss1_sigma, gauss2_center) = -0.9918
C(gauss1_sigma, gauss3_amplitude) = -0.1030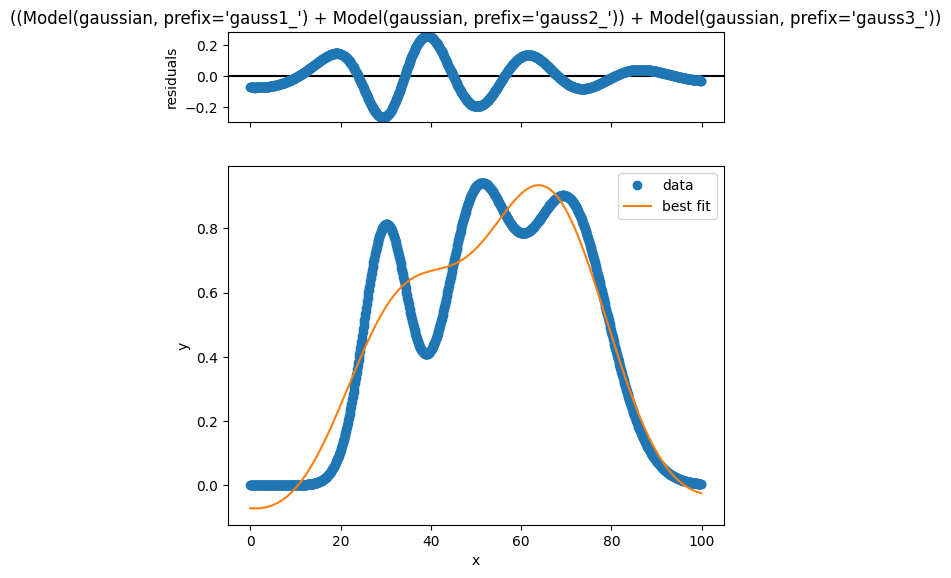
三つのガウス関数に対してそれぞれパラメータが存在するので結果が大量に出てきます。
R-squaredは先ほどよりだいぶ良くなっており、0.90160458と1にだいぶ近くなっています。
しかしパラメータをちゃんと見てみると元のグラフを作成する際に設定したパラメータとはかけ離れています。
[[Variables]]
gauss1_amplitude: -179292.534 +/- 1.7249e+10 (9620532.86%) (init = 1)
gauss1_center: 49.5653927 +/- 343.743740 (693.52%) (init = 0)
gauss1_sigma: 17.9942836 +/- 3336.62719 (18542.71%) (init = 1)
gauss2_amplitude: -180962.322 +/- 1.7189e+10 (9498652.13%) (init = 1)
gauss2_center: 49.5837797 +/- 245.193463 (494.50%) (init = 0)
gauss2_sigma: 17.7889338 +/- 3226.36666 (18136.93%) (init = 1)
gauss3_amplitude: 360298.312 +/- 1.3536e+09 (375687.29%) (init = 1)
gauss3_center: 49.5753212 +/- 586.144788 (1182.33%) (init = 0)
gauss3_sigma: 17.8910754 +/- 6549.60193 (36608.21%) (init = 1)
gauss1_fwhm: 42.3732988 +/- 7857.15640 (18542.71%) == '2.3548200*gauss1_sigma'
gauss1_height: -3975.00549 +/- 3.8315e+08 (9639072.00%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_fwhm: 41.8897371 +/- 7597.51271 (18136.93%) == '2.3548200*gauss2_sigma'
gauss2_height: -4058.33907 +/- 3.8475e+08 (9480518.63%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_fwhm: 42.1302615 +/- 15423.1336 (36608.21%) == '2.3548200*gauss3_sigma'
gauss3_height: 8034.07489 +/- 30196195.6 (375851.56%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)三つのガウス関数がどんな分布になっているのか分離して表示してみましょう。
複数の分布を含んだモデルをそれぞれの関数に分離する場合は「model.fitの返り値.eval_components(x=X値のリスト)」とします。
そしてそれぞれの分布のY値のリストは、分離した返り値に対して先ほどつけたそれぞれの関数の名前(prefix)を使って辞書形式で取得します。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.GaussianModel(prefix="gauss2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model.make_params()
output = model.fit(y_test, params, x=x_list)
comps = output.eval_components(x=x_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_test, label="test")
plt.plot(x_list, output.best_fit, label="best_fit")
plt.plot(x_list, comps["gauss1_"], ls="--")
plt.plot(x_list, comps["gauss2_"], ls="--")
plt.plot(x_list, comps["gauss3_"], ls="--")
plt.legend()
plt.show()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(gaussian, prefix='gauss2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 4054
# data points = 1000
# variables = 9
chi-square = 12.2530813
reduced chi-square = 0.01236436
Akaike info crit = -4383.97784
Bayesian info crit = -4339.80804
R-squared = 0.90160458
[[Variables]]
gauss1_amplitude: -179292.534 +/- 1.7249e+10 (9620532.86%) (init = 1)
gauss1_center: 49.5653927 +/- 343.743740 (693.52%) (init = 0)
gauss1_sigma: 17.9942836 +/- 3336.62719 (18542.71%) (init = 1)
gauss2_amplitude: -180962.322 +/- 1.7189e+10 (9498652.13%) (init = 1)
gauss2_center: 49.5837797 +/- 245.193463 (494.50%) (init = 0)
gauss2_sigma: 17.7889338 +/- 3226.36666 (18136.93%) (init = 1)
gauss3_amplitude: 360298.312 +/- 1.3536e+09 (375687.29%) (init = 1)
gauss3_center: 49.5753212 +/- 586.144788 (1182.33%) (init = 0)
gauss3_sigma: 17.8910754 +/- 6549.60193 (36608.21%) (init = 1)
gauss1_fwhm: 42.3732988 +/- 7857.15640 (18542.71%) == '2.3548200*gauss1_sigma'
gauss1_height: -3975.00549 +/- 3.8315e+08 (9639072.00%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_fwhm: 41.8897371 +/- 7597.51271 (18136.93%) == '2.3548200*gauss2_sigma'
gauss2_height: -4058.33907 +/- 3.8475e+08 (9480518.63%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_fwhm: 42.1302615 +/- 15423.1336 (36608.21%) == '2.3548200*gauss3_sigma'
gauss3_height: 8034.07489 +/- 30196195.6 (375851.56%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(gauss3_center, gauss3_sigma) = -1.0000
C(gauss1_center, gauss1_sigma) = -1.0000
C(gauss2_center, gauss2_sigma) = -0.9999
C(gauss1_amplitude, gauss1_center) = -0.9999
C(gauss2_amplitude, gauss2_sigma) = -0.9998
C(gauss1_amplitude, gauss1_sigma) = +0.9998
C(gauss2_amplitude, gauss2_center) = +0.9995
C(gauss1_amplitude, gauss3_center) = +0.9994
C(gauss1_amplitude, gauss3_sigma) = -0.9992
C(gauss2_amplitude, gauss3_sigma) = +0.9992
C(gauss2_amplitude, gauss3_center) = -0.9990
C(gauss1_center, gauss3_center) = -0.9989
C(gauss1_center, gauss3_sigma) = +0.9987
C(gauss1_sigma, gauss3_center) = +0.9985
C(gauss2_sigma, gauss3_sigma) = -0.9983
C(gauss1_sigma, gauss3_sigma) = -0.9983
C(gauss2_sigma, gauss3_center) = +0.9980
C(gauss2_center, gauss3_sigma) = +0.9976
C(gauss2_center, gauss3_center) = -0.9973
C(gauss1_amplitude, gauss2_amplitude) = -0.9969
C(gauss1_center, gauss2_amplitude) = +0.9959
C(gauss1_amplitude, gauss2_sigma) = +0.9952
C(gauss1_sigma, gauss2_amplitude) = -0.9952
C(gauss1_amplitude, gauss2_center) = -0.9941
C(gauss1_center, gauss2_sigma) = -0.9939
C(gauss1_sigma, gauss2_sigma) = +0.9931
C(gauss1_center, gauss2_center) = +0.9927
C(gauss1_sigma, gauss2_center) = -0.9918
C(gauss1_sigma, gauss3_amplitude) = -0.1030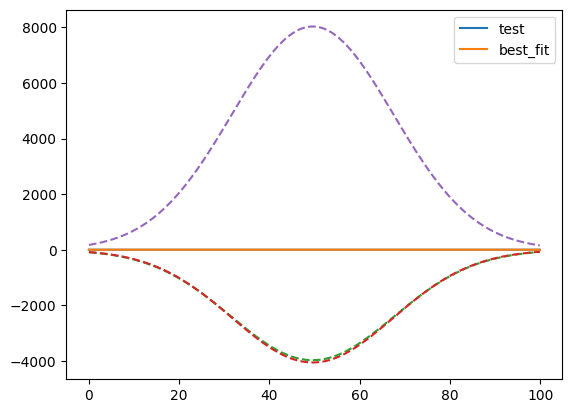
元の三つのガウス分布からはかけ離れた分布となってしまいました。
複数のピークに対してフィッティングする際、この様に表面上はフィッティングできている様に見えても、それぞれの分布に対して正しくフィッティングできていない場合があるので注意しましょう。
複数のモデルに対してそれぞれ初期パラメータを設定する方法
正しくフィッティングするためにはなるべく正しい初期パラメータを与えることが大切です。
前回の様に1つの関数に対して初期パラメータを与える場合、「model.make_params(パラメータ名1=初期パラメータ1, パラメータ名2=初期パラメータ2…)」という感じで与えました。
今回の様に複数の関数がある場合はまずはパラメータ情報を1つにまとめてしまいます。
params = model1.make_params()
params.update(model2.make_params())
params.update(model3.make_params())そして先ほど指定したモデル名(prefix)とパラメータ名を使い、パラメータをセットしていきます。
例えばprefix名が「gauss1_」で頂点の位置を示す「center」に対して初期パラメータを設定したい場合、「params[“gauss1_center”].set(値)」という感じになります。
ということでプログラムとしてはこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.GaussianModel(prefix="gauss2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model1.make_params()
params.update(model2.make_params())
params.update(model3.make_params())
params["gauss1_center"].set(30)
params["gauss2_center"].set(50)
params["gauss3_center"].set(70)
output = model.fit(y_test, params, x=x_list)
comps = output.eval_components(x=x_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_test, label="test")
plt.plot(x_list, output.best_fit, label="best_fit")
plt.plot(x_list, comps["gauss1_"], ls="--")
plt.plot(x_list, comps["gauss2_"], ls="--")
plt.plot(x_list, comps["gauss3_"], ls="--")
plt.legend()
plt.show()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(gaussian, prefix='gauss2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 101
# data points = 1000
# variables = 9
chi-square = 3.9632e-29
reduced chi-square = 3.9992e-32
Akaike info crit = -72287.6666
Bayesian info crit = -72243.4968
R-squared = 1.00000000
[[Variables]]
gauss1_amplitude: 10.00000000 +/- 4.9588e-16 (0.00%) (init = 1)
gauss1_center: 30.0000000 +/- 2.6006e-16 (0.00%) (init = 30)
gauss1_sigma: 5.00000000 +/- 2.5301e-16 (0.00%) (init = 1)
gauss1_fwhm: 11.7741000 +/- 5.9580e-16 (0.00%) == '2.3548200*gauss1_sigma'
gauss1_height: 0.79788460 +/- 2.6481e-17 (0.00%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_amplitude: 15.0000000 +/- 1.6158e-15 (0.00%) (init = 1)
gauss2_center: 50.0000000 +/- 5.4500e-16 (0.00%) (init = 50)
gauss2_sigma: 7.00000000 +/- 5.6749e-16 (0.00%) (init = 1)
gauss2_fwhm: 16.4837400 +/- 1.3363e-15 (0.00%) == '2.3548200*gauss2_sigma'
gauss2_height: 0.85487636 +/- 3.8121e-17 (0.00%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_amplitude: 20.0000000 +/- 1.4763e-15 (0.00%) (init = 1)
gauss3_center: 70.0000000 +/- 7.4269e-16 (0.00%) (init = 70)
gauss3_sigma: 9.00000000 +/- 5.6187e-16 (0.00%) (init = 1)
gauss3_fwhm: 21.1933797 +/- 1.3231e-15 (0.00%) == '2.3548200*gauss3_sigma'
gauss3_height: 0.88653846 +/- 2.4839e-17 (0.00%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(gauss2_amplitude, gauss3_amplitude) = -0.9323
C(gauss3_amplitude, gauss3_sigma) = +0.9289
C(gauss2_amplitude, gauss3_center) = +0.9282
C(gauss2_amplitude, gauss2_sigma) = +0.9268
C(gauss3_amplitude, gauss3_center) = -0.9090
C(gauss2_amplitude, gauss3_sigma) = -0.8667
C(gauss2_center, gauss3_center) = +0.8618
C(gauss2_center, gauss3_amplitude) = -0.8618
C(gauss3_center, gauss3_sigma) = -0.8533
C(gauss2_sigma, gauss3_center) = +0.8357
C(gauss2_sigma, gauss3_amplitude) = -0.8322
C(gauss2_center, gauss3_sigma) = -0.8270
C(gauss2_amplitude, gauss2_center) = +0.7882
C(gauss1_amplitude, gauss1_sigma) = +0.7807
C(gauss2_sigma, gauss3_sigma) = -0.7130
C(gauss1_amplitude, gauss2_sigma) = -0.6637
C(gauss2_center, gauss2_sigma) = +0.6554
C(gauss1_center, gauss2_sigma) = -0.6090
C(gauss1_amplitude, gauss2_amplitude) = -0.5768
C(gauss1_sigma, gauss2_sigma) = -0.5397
C(gauss1_center, gauss2_amplitude) = -0.5275
C(gauss1_amplitude, gauss1_center) = +0.5197
C(gauss1_sigma, gauss2_amplitude) = -0.4680
C(gauss1_center, gauss1_sigma) = +0.4558
C(gauss1_amplitude, gauss3_center) = -0.4425
C(gauss1_amplitude, gauss3_amplitude) = +0.4410
C(gauss1_center, gauss3_center) = -0.4053
C(gauss1_center, gauss3_amplitude) = +0.4039
C(gauss1_amplitude, gauss3_sigma) = +0.3545
C(gauss1_sigma, gauss3_center) = -0.3362
C(gauss1_sigma, gauss3_amplitude) = +0.3354
C(gauss1_center, gauss3_sigma) = +0.3243
C(gauss1_sigma, gauss3_sigma) = +0.2651
C(gauss1_amplitude, gauss2_center) = -0.1873
C(gauss1_center, gauss2_center) = -0.1722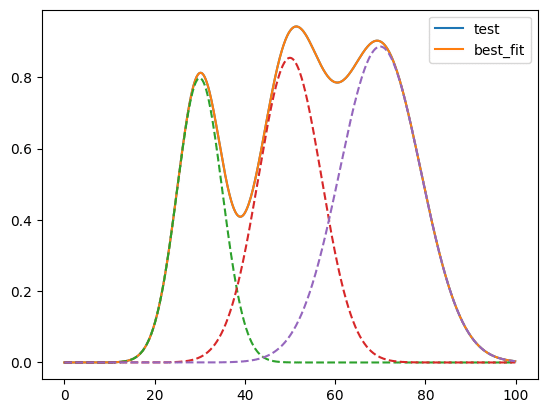
これでR-squaredも1.00000000となり、フィッティング前後で完全に一致しましたし、それぞれ分離したグラフを見ても元のグラフと一緒の様です。
また初期パラメータに関しては特定の値以外にも最大値、最小値を設定することができます。
その場合は「params[“gauss1_center”].set(value=初期値, min=最小値, max=最大値)」の様に記述します。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
gaussian2 = gaussian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + gaussian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.GaussianModel(prefix="gauss2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model1.make_params()
params.update(model2.make_params())
params.update(model3.make_params())
params["gauss1_center"].set(value=30, min=25, max=35)
params["gauss2_center"].set(value=50, min=45, max=55)
params["gauss3_center"].set(value=70, min=65, max=75)
output = model.fit(y_test, params, x=x_list)
comps = output.eval_components(x=x_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_test, label="test")
plt.plot(x_list, output.best_fit, label="best_fit")
plt.plot(x_list, comps["gauss1_"], ls="--")
plt.plot(x_list, comps["gauss2_"], ls="--")
plt.plot(x_list, comps["gauss3_"], ls="--")
plt.legend()
plt.show()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(gaussian, prefix='gauss2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 91
# data points = 1000
# variables = 9
chi-square = 4.4486e-19
reduced chi-square = 4.4890e-22
Akaike info crit = -49146.2872
Bayesian info crit = -49102.1174
R-squared = 1.00000000
[[Variables]]
gauss1_amplitude: 10.00000000 +/- 5.2651e-11 (0.00%) (init = 1)
gauss1_center: 30.0000000 +/- 2.6572e-11 (0.00%) (init = 30)
gauss1_sigma: 5.00000000 +/- 2.6808e-11 (0.00%) (init = 1)
gauss1_fwhm: 11.7741000 +/- 6.3127e-11 (0.00%) == '2.3548200*gauss1_sigma'
gauss1_height: 0.79788460 +/- 2.8131e-12 (0.00%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_amplitude: 15.0000000 +/- 1.6921e-10 (0.00%) (init = 1)
gauss2_center: 50.0000000 +/- 4.7051e-11 (0.00%) (init = 50)
gauss2_sigma: 7.00000000 +/- 5.9808e-11 (0.00%) (init = 1)
gauss2_fwhm: 16.4837400 +/- 1.4084e-10 (0.00%) == '2.3548200*gauss2_sigma'
gauss2_height: 0.85487636 +/- 3.9779e-12 (0.00%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_amplitude: 20.0000000 +/- 1.5408e-10 (0.00%) (init = 1)
gauss3_center: 70.0000000 +/- 7.4557e-11 (0.00%) (init = 70)
gauss3_sigma: 9.00000000 +/- 5.8564e-11 (0.00%) (init = 1)
gauss3_fwhm: 21.1933797 +/- 1.3791e-10 (0.00%) == '2.3548200*gauss3_sigma'
gauss3_height: 0.88653846 +/- 2.6296e-12 (0.00%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(gauss2_amplitude, gauss3_amplitude) = -0.9307
C(gauss3_amplitude, gauss3_sigma) = +0.9265
C(gauss2_amplitude, gauss2_sigma) = +0.9265
C(gauss2_amplitude, gauss3_center) = +0.9264
C(gauss3_amplitude, gauss3_center) = -0.9063
C(gauss2_amplitude, gauss3_sigma) = -0.8630
C(gauss2_center, gauss3_center) = +0.8577
C(gauss2_center, gauss3_amplitude) = -0.8573
C(gauss3_center, gauss3_sigma) = -0.8486
C(gauss2_sigma, gauss3_center) = +0.8343
C(gauss2_sigma, gauss3_amplitude) = -0.8307
C(gauss2_center, gauss3_sigma) = -0.8207
C(gauss2_amplitude, gauss2_center) = +0.7825
C(gauss1_amplitude, gauss1_sigma) = +0.7800
C(gauss2_sigma, gauss3_sigma) = -0.7087
C(gauss1_amplitude, gauss2_sigma) = -0.6707
C(gauss2_center, gauss2_sigma) = +0.6508
C(gauss1_center, gauss2_sigma) = -0.6141
C(gauss1_amplitude, gauss2_amplitude) = -0.5873
C(gauss1_sigma, gauss2_sigma) = -0.5407
C(gauss1_center, gauss2_amplitude) = -0.5356
C(gauss1_amplitude, gauss1_center) = +0.5214
C(gauss1_sigma, gauss2_amplitude) = -0.4707
C(gauss1_center, gauss1_sigma) = +0.4559
C(gauss1_amplitude, gauss3_center) = -0.4531
C(gauss1_amplitude, gauss3_amplitude) = +0.4517
C(gauss1_center, gauss3_center) = -0.4131
C(gauss1_center, gauss3_amplitude) = +0.4118
C(gauss1_amplitude, gauss3_sigma) = +0.3637
C(gauss1_sigma, gauss3_center) = -0.3377
C(gauss1_sigma, gauss3_amplitude) = +0.3371
C(gauss1_center, gauss3_sigma) = +0.3308
C(gauss1_sigma, gauss3_sigma) = +0.2659
C(gauss1_amplitude, gauss2_center) = -0.1963
C(gauss1_center, gauss2_center) = -0.1780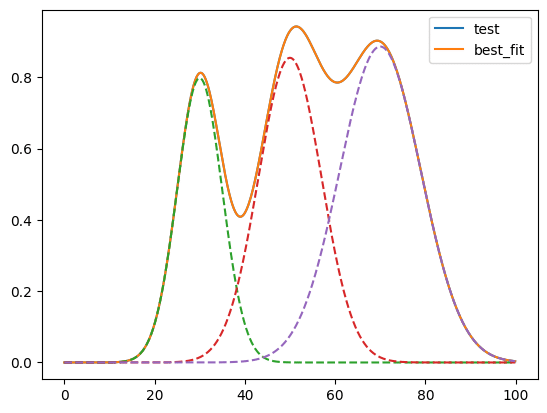
ここまでは3つのガウス分布を足し合わせたグラフに対してフィッティングしてきましたが、他の分布が混ざっていてもモデルが合っていれば、かなりの精度でフィッティングしてくれます
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian, lorentzian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
lorentzian2 = lorentzian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + lorentzian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.LorentzianModel(prefix="lorentzian2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model1.make_params()
params.update(model2.make_params())
params.update(model3.make_params())
params["gauss1_center"].set(value=30, min=25, max=35)
params["lorentzian2_center"].set(value=50, min=45, max=55)
params["gauss3_center"].set(value=70, min=65, max=75)
output = model.fit(y_test, params, x=x_list)
comps = output.eval_components(x=x_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_test, label="test")
plt.plot(x_list, output.best_fit, label="best_fit")
plt.plot(x_list, comps["gauss1_"], ls="--")
plt.plot(x_list, comps["lorentzian2_"], ls="--")
plt.plot(x_list, comps["gauss3_"], ls="--")
plt.legend()
plt.show()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(lorentzian, prefix='lorentzian2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 113
# data points = 1000
# variables = 9
chi-square = 4.7249e-20
reduced chi-square = 4.7678e-23
Akaike info crit = -51388.6131
Bayesian info crit = -51344.4433
R-squared = 1.00000000
## Warning: uncertainties could not be estimated:
gauss1_center: at initial value
lorentzian2_center: at initial value
gauss3_center: at initial value
[[Variables]]
gauss1_amplitude: 10.0000000 (init = 1)
gauss1_center: 30.0000000 (init = 30)
gauss1_sigma: 5.00000000 (init = 1)
gauss1_fwhm: 11.7741000 == '2.3548200*gauss1_sigma'
gauss1_height: 0.79788460 == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
lorentzian2_amplitude: 15.0000000 (init = 1)
lorentzian2_center: 50.0000000 (init = 50)
lorentzian2_sigma: 7.00000000 (init = 1)
lorentzian2_fwhm: 14.0000000 == '2.0000000*lorentzian2_sigma'
lorentzian2_height: 0.68209264 == '0.3183099*lorentzian2_amplitude/max(1e-15, lorentzian2_sigma)'
gauss3_amplitude: 20.0000000 (init = 1)
gauss3_center: 70.0000000 (init = 70)
gauss3_sigma: 9.00000000 (init = 1)
gauss3_fwhm: 21.1933800 == '2.3548200*gauss3_sigma'
gauss3_height: 0.88653844 == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'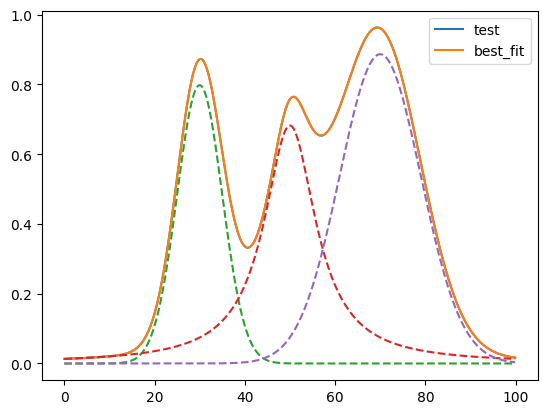
与えるモデルが間違っているとやはりフィッティング精度が落ちることとなるので、分布がどんな関数で成り立っているのかを考えることは重要です。
試しに上記の「ガウス分布+ローレンツ分布+ガウス分布」の足し合わせの分布を「ガウス関数+ガウス関数+ガウス関数」のモデルでフィッティングしてみます。
import numpy as np
import matplotlib.pyplot as plt
from lmfit.lineshapes import gaussian, lorentzian
from lmfit import models
x_list = np.arange(0, 100, 0.1)
gaussian1 = gaussian(x_list, 10, 30, 5)
lorentzian2 = lorentzian(x_list, 15, 50, 7)
gaussian3 = gaussian(x_list, 20, 70, 9)
y_test = gaussian1 + lorentzian2 + gaussian3
model1 = models.GaussianModel(prefix="gauss1_")
model2 = models.GaussianModel(prefix="gauss2_")
model3 = models.GaussianModel(prefix="gauss3_")
model = model1 + model2 + model3
params = model1.make_params()
params.update(model2.make_params())
params.update(model3.make_params())
params["gauss1_center"].set(value=30, min=25, max=35)
params["gauss2_center"].set(value=50, min=45, max=55)
params["gauss3_center"].set(value=70, min=65, max=75)
output = model.fit(y_test, params, x=x_list)
comps = output.eval_components(x=x_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_test, label="test")
plt.plot(x_list, output.best_fit, label="best_fit")
plt.plot(x_list, comps["gauss1_"], ls="--")
plt.plot(x_list, comps["gauss2_"], ls="--")
plt.plot(x_list, comps["gauss3_"], ls="--")
plt.legend()
plt.show()
print(output.fit_report())
実行結果
[[Model]]
((Model(gaussian, prefix='gauss1_') + Model(gaussian, prefix='gauss2_')) + Model(gaussian, prefix='gauss3_'))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 103
# data points = 1000
# variables = 9
chi-square = 0.09839046
reduced chi-square = 9.9284e-05
Akaike info crit = -9208.56673
Bayesian info crit = -9164.39693
R-squared = 0.99909451
[[Variables]]
gauss1_amplitude: 11.8754534 +/- 0.02118603 (0.18%) (init = 1)
gauss1_center: 30.3319886 +/- 0.01082077 (0.04%) (init = 30)
gauss1_sigma: 5.48431381 +/- 0.01157910 (0.21%) (init = 1)
gauss1_fwhm: 12.9145718 +/- 0.02726670 (0.21%) == '2.3548200*gauss1_sigma'
gauss1_height: 0.86384931 +/- 0.00125917 (0.15%) == '0.3989423*gauss1_amplitude/max(1e-15, gauss1_sigma)'
gauss2_amplitude: 8.25056255 +/- 0.04540920 (0.55%) (init = 1)
gauss2_center: 49.5067499 +/- 0.02019741 (0.04%) (init = 50)
gauss2_sigma: 5.36506558 +/- 0.02283476 (0.43%) (init = 1)
gauss2_fwhm: 12.6337637 +/- 0.05377176 (0.43%) == '2.3548200*gauss2_sigma'
gauss2_height: 0.61350572 +/- 0.00175207 (0.29%) == '0.3989423*gauss2_amplitude/max(1e-15, gauss2_sigma)'
gauss3_amplitude: 23.2078563 +/- 0.04590716 (0.20%) (init = 1)
gauss3_center: 69.2502782 +/- 0.02152264 (0.03%) (init = 70)
gauss3_sigma: 9.60081358 +/- 0.02051238 (0.21%) (init = 1)
gauss3_fwhm: 22.6081875 +/- 0.04830295 (0.21%) == '2.3548200*gauss3_sigma'
gauss3_height: 0.96435533 +/- 9.7288e-04 (0.10%) == '0.3989423*gauss3_amplitude/max(1e-15, gauss3_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(gauss3_amplitude, gauss3_sigma) = +0.8826
C(gauss2_amplitude, gauss2_sigma) = +0.8591
C(gauss2_amplitude, gauss3_amplitude) = -0.8373
C(gauss2_amplitude, gauss3_center) = +0.8298
C(gauss2_amplitude, gauss3_sigma) = -0.8042
C(gauss3_amplitude, gauss3_center) = -0.7537
C(gauss1_amplitude, gauss1_sigma) = +0.7322
C(gauss3_center, gauss3_sigma) = -0.7226
C(gauss2_sigma, gauss3_center) = +0.6872
C(gauss2_sigma, gauss3_amplitude) = -0.6725
C(gauss2_center, gauss3_center) = +0.6451
C(gauss2_center, gauss3_amplitude) = -0.6397
C(gauss2_center, gauss3_sigma) = -0.6120
C(gauss2_sigma, gauss3_sigma) = -0.5851
C(gauss2_amplitude, gauss2_center) = +0.5232
C(gauss1_amplitude, gauss2_sigma) = -0.4924
C(gauss1_sigma, gauss2_sigma) = -0.4855
C(gauss1_center, gauss2_sigma) = -0.4635
C(gauss1_sigma, gauss2_amplitude) = -0.4081
C(gauss1_amplitude, gauss2_amplitude) = -0.4051
C(gauss1_center, gauss2_amplitude) = -0.3770
C(gauss2_center, gauss2_sigma) = +0.3482
C(gauss1_center, gauss1_sigma) = +0.3354
C(gauss1_amplitude, gauss1_center) = +0.3242
C(gauss1_amplitude, gauss3_center) = -0.2320
C(gauss1_center, gauss3_center) = -0.2234
C(gauss1_amplitude, gauss3_amplitude) = +0.2233
C(gauss1_sigma, gauss3_center) = -0.2202
C(gauss1_center, gauss3_amplitude) = +0.2151
C(gauss1_sigma, gauss3_amplitude) = +0.2124
C(gauss1_amplitude, gauss3_sigma) = +0.1797
C(gauss1_center, gauss3_sigma) = +0.1738
C(gauss1_sigma, gauss3_sigma) = +0.1713
C(gauss1_sigma, gauss2_center) = +0.1545
C(gauss1_amplitude, gauss2_center) = +0.1161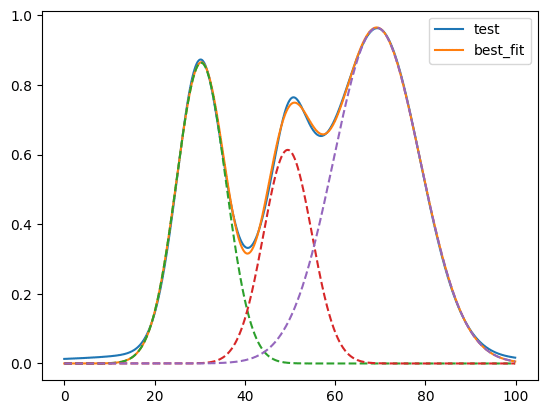
「R-squared = 0.99909451」とほんの少し悪化しました。
今回はガウス分布とローレンツ分布はかなり似通っているのでR-squaredではほんの少しの悪化で済みました。
ただしこの差がどれくらい重要かはこのフィッティング結果をどう使っていくかによって変わってくると思います。
なのでちゃんとフィッティングが完全にはできていない場合は十分なフィッティングなのか、そうでないのかはちゃんと見極める必要があるでしょう。
次回はlmfitの左右非対称のフォークト関数であるSkewedVoigtModelを試してみます。
ではでは今回はこんな感じで。

コメント