mathモジュール
前回、Pythonプログラムのファイル名をライブラリ名にした時に起こるエラーに関して紹介しました。
今回は数学計算用モジュールである「math」を色々試してみようと思います。
mathモジュールはPythonの標準ライブラリの一つなのでインストールせずに使用することができます。
それでは始めていきましょう。
定数: π、tau、e、inf、nan
まずは数学で用いる定数からです。
円周率のπ、円周率の2倍であるtau、自然対数の底e、無限大のinf、欠損値のnanなどがあります。
import math
print(math.pi)
print(math.tau)
print(math.e)
print(math.inf)
print(math.nan)
実行結果
3.141592653589793
6.283185307179586
2.718281828459045
inf
nan切り上げceil、切り下げfloor、小数部を取り除くtrunc、小数部分と整数部分を返すmodf
小数を常に大きな方の整数に切り上げるには「ceil」、常に小さな方の整数に切り下げるには「floor」を用います。
import math
print(math.ceil(1.2))
print(math.ceil(-1.2))
print(math.floor(1.2))
print(math.floor(-1.2))
実行結果
2
-1
1
-2ちなみに小数から整数に変更する際の小数点以下の取り扱い(切り捨て、四捨五入、切り上げ、切り下げ)に関してはこちらの記事で解説していますので、よかったらどうぞ。

また小数部分を取り除き、整数部分だけにする場合は「trunc」を用います。
import math
print(math.trunc(1.23))
print(math.trunc(-1.23))
実行結果
1
-1小数部分、整数部分をそれぞれ取得する場合は「modf」を用います。
import math
print(math.modf(5.12))
print(math.modf(-5.12))
実行結果
(0.1200000000000001, 5.0)
(-0.1200000000000001, -5.0)絶対値fabs
mathモジュールで絶対値を取得する場合は「fabs」を用います。
import math
print(math.fabs(10))
print(math.fabs(-10))
実行結果
10.0
10.0mathモジュールのfabsではfloatとして返されるのが特徴です。
また絶対値を取得するには「abs」、numpyの「abs」などもあります。
print(abs(10))
print(abs(-10))
実行結果
10
10import numpy as np
print(np.abs(10))
print(np.abs(-10))
実行結果
10
10これらの場合はintとして返ってきます。
階乗factorial
ある数の階乗を取得するには「factorial」を用います。
import math
print(math.factorial(3))
print(math.factorial(5))
実行結果
6
120ちなみに小数値や負の値ではエラーとなります。
import math
print(math.factorial(3.1))
実行結果
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[23], line 3
1 import math
----> 3 print(math.factorial(3.1))
TypeError: 'float' object cannot be interpreted as an integerimport math
print(math.factorial(-3))
実行結果
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[24], line 3
1 import math
----> 3 print(math.factorial(-3))
ValueError: factorial() not defined for negative values最大公約数gcd
複数の値の最大公約数を取得するには「gcd 」を用います。
import math
print(math.gcd(6, 9))
print(math.gcd(6, 9, 18))
実行結果
3
3最大公倍数lcm
複数の値の最大公倍数を取得するには「lcm」を用います。
import math
print(math.lcm(2, 3))
print(math.lcm(2, 3, 4))
実行結果
6
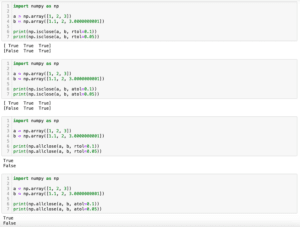
12近い値かどうかを判定isclose
二つの値が近い値かどうかを判定するにはiscloseを用います。
import math
print(math.isclose(2, 2.1))
print(math.isclose(2, 2.3))
実行結果
False
False相対許容差を指定するには「rel_tol」のオプションを追加します。
例えば許容差を5%に設定する場合は「rel_tol=0.05」とします。
デフォルト値は1e-9です。
import math
print(math.isclose(2, 2.1, rel_tol=0.05))
print(math.isclose(2, 2.3, rel_tol=0.05))
実行結果
True
False最小の絶対許容差を指定するには「abs_tol」のオプションを追加します。
import math
print(math.isclose(2, 2.5, abs_tol=1))
print(math.isclose(2, 3.1, abs_tol=1))
実行結果
True
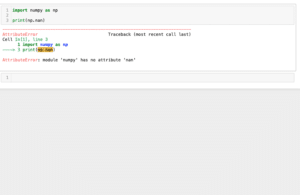
False欠損値nanかどうかを判定isnan
欠損値nanかどうかを判定するには「isnan」を用います。
これはnumpyの「isnan」と同じ結果を返します。
import math
import numpy as np
x = np.nan
y = 5
print(math.isnan(x))
print(math.isnan(y))
print(np.isnan(x))
print(np.isnan(y))
実行結果
True
False
True
False全ての要素の積prod
全ての要素の積を計算するには「prod」を用います。
import math
print(math.prod([2, 3]))
print(math.prod([2, 3, 4]))
実行結果
6
24対数:log、log2、log10
対数は「log(値, 底)」で計算します。
底を指定しない場合、底は自然対数の底eとなります。
import math
print(math.log(2))
print(math.log(8, 2))
実行結果
0.6931471805599453
3.0ただし底が「2」と「10」の場合は「log2(値)」、「log10(値)」を用いることもできます。
import math
print(math.log2(8))
print(math.log10(1000))
実行結果
3.0
3.0指数pow
指数は「pow(値, 乗数)」を用います。
ちなみにmathモジュールを用いなくても指数の計算ができます。
import math
print(math.pow(2,3))
print(pow(2,3))
実行結果
8.0
8mathモジュールを用いた場合はfloat値として、用いていない場合はint値として返ってくることに注意です。
平方根sqrt
平方根を計算するには「sqrt」を用います。
import math
print(math.sqrt(4))
実行結果
2.0numpynのsqrtでも計算できます。
import numpy as np
print(np.sqrt(4))
実行結果
2.0ラジアン→角度degrees、角度→ラジアンradians
ラジアンを角度に変換するには「degrees」、角度をラジアンに変換するには「radians」を使います。
import math
print(math.degrees(math.pi/2))
print(math.radians(90))
実行結果
90.0
1.5707963267948966三角関数sin, cos, tan、逆三角関数asin, acos, atan
三角関数はそれぞれ「sin」、「cos」、「tan」を用います。
この際、角度はラジアンで指定します。
import math
print(math.degrees(math.pi/4))
print(math.sin(math.pi/4))
print(math.cos(math.pi/4))
print(math.tan(math.pi/4))
実行結果
45.0
0.7071067811865475
0.7071067811865476
0.9999999999999999逆三角関数は「asin」、「acos」、「atan」を用い、こちらも角度はラジアンで指定します。
import math
print(math.degrees(math.pi/4))
print(math.asin(math.pi/4))
print(math.acos(math.pi/4))
print(math.atan(math.pi/4))
実行結果
45.0
0.9033391107665127
0.6674572160283838
0.6657737500283538次回はnumpyで値が近いかどうかを判定するiscloseを紹介します。
ではでは今回はこんな感じで。

コメント