NumPy
前回、PythonのNumPyで畳み込み積分と移動平均を計算する「np.convolve」を紹介しました。
今回はnp.convolveで指定する3種類の「mode」、「same」と「full」と「valid」を比較してみたので、その結果を紹介します。
結果がわかりやすいように移動平均を使って比較してみます。
「np.convolve」を使って移動平均を計算する方法は前回紹介しましたので、そちらの記事をご覧ください。
ということでこんな感じのグラフを作成してみました。
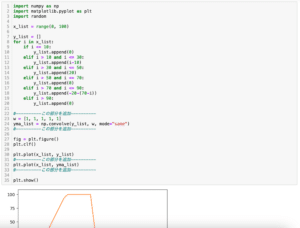
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
plt.show()
実行結果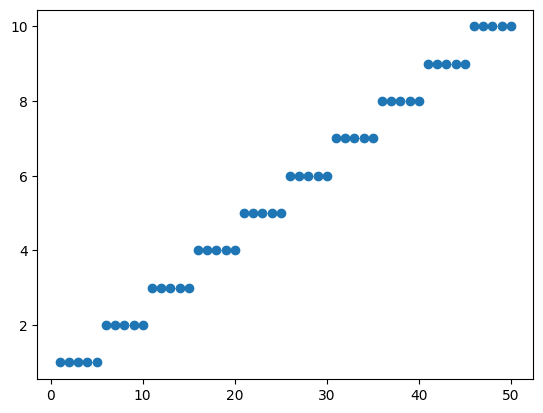
それでは始めていきましょう。
same
まずは前回も使用した「same」です。
移動平均なので畳み込み演算の窓としては「1/n, 1/n, 1/n .. 1/n, 1/n」(nは窓の長さ)という形になります。
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
#----------この部分を追加----------
window = 5
w = np.ones(window)/window
y_cov = np.convolve(y, w, mode="same")
print(y_cov)
#----------この部分を追加----------
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
#----------この部分を追加----------
plt.scatter(x, y_cov)
#----------この部分を追加----------
plt.show()
実行結果
[ 0.6 0.8 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2
3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8 5. 5.2 5.4 5.6 5.8 6.
6.2 6.4 6.6 6.8 7. 7.2 7.4 7.6 7.8 8. 8.2 8.4 8.6 8.8
9. 9.2 9.4 9.6 9.8 10. 8. 6. ]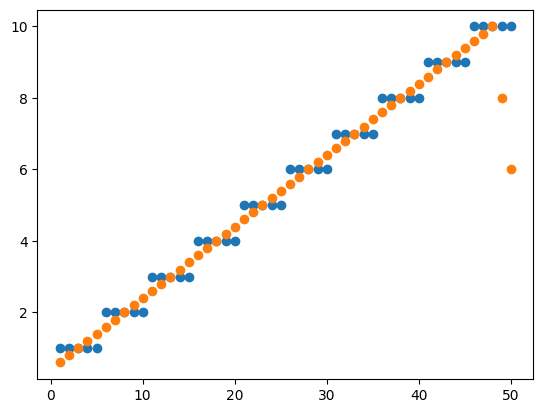
グラフを見てパッと分かることは、元のグラフの中心を通っていること、またグラフの最初と最後が元の数値よりも小さくなっていることです。
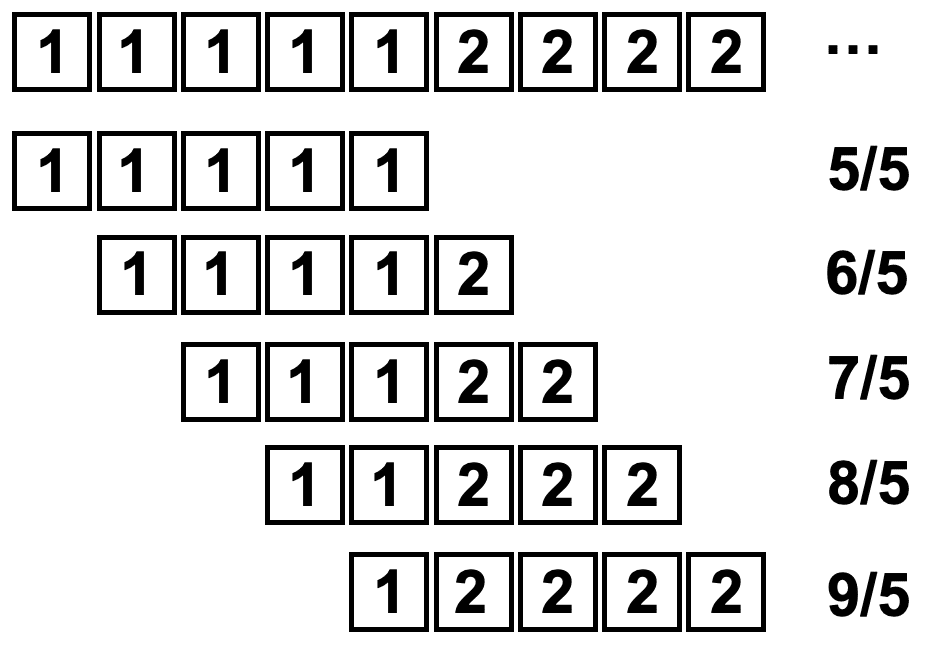
数値を確認してみると移動平均を取得した最初の5点は「0.6, 0.8, 1, 1.2, 1.4」で、最後の5点は「9.6, 9.8, 10, 8, 6」でした。
最初の5点を順に計算していくと「0, 0, 1, 1, 1」=3/5=0.6、「0, 1, 1, 1, 1」=4/5=0.8、「1, 1, 1, 1, 1」=1、「1, 1, 1, 1, 2」=6/5=1.2、「1, 1, 1, 2, 2」=7/5=1.4ということが分かります。
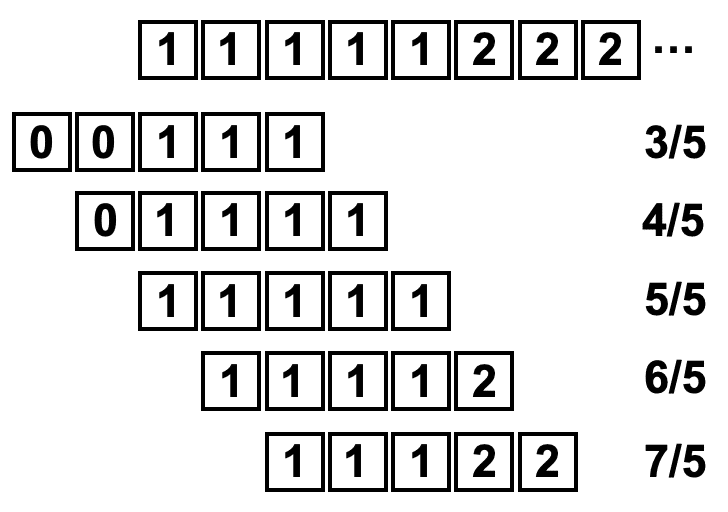
つまり窓の長さ5に対し、真ん中の点が元のグラフの最初になるように配置され、飛び出た部分は0になっていることが分かります。
最後の5点を計算してみると「9, 9, 10, 10, 10」=48/5=9.6、「9, 10, 10, 10, 10」=49/5=9.8、「10, 10, 10, 10, 10」=50/5=10、「10, 10, 10, 10, 0」=40/5=8、「10, 10, 10, 0, 0」=30/5=6となっています。
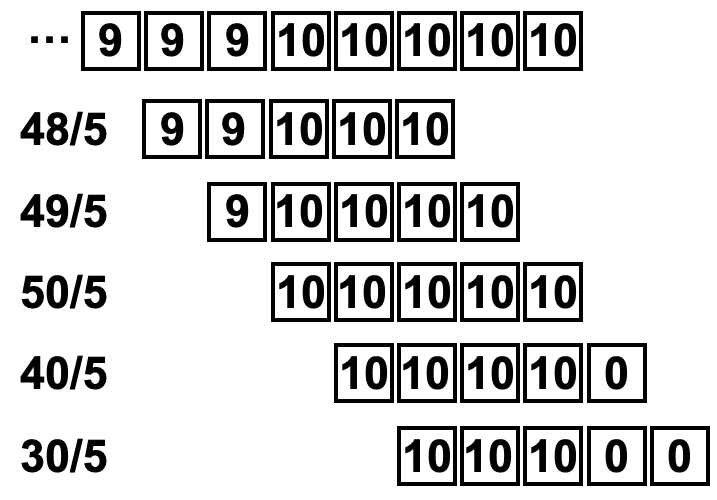
ということで「same」は窓の真ん中が畳み込むデータの端になるようにするモードということが分かりました。
この場合、元のデータ数と畳み込み後のデータ数が一緒になるというメリットがありますが、末端の数値は当てにならないことがデメリットとなります。
full
次に「full」を試してみましょう。
単純に先ほどのプログラムのnp.convolveのモードを「full」に変えてみます。
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
window = 5
w = np.ones(window)/window
#----------この部分を変更----------
y_cov = np.convolve(y, w, mode="full")
#----------この部分を変更----------
print(y_cov)
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
plt.scatter(x, y_cov)
plt.show()
実行結果
[ 0.2 0.4 0.6 0.8 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8
3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8 5. 5.2 5.4 5.6
5.8 6. 6.2 6.4 6.6 6.8 7. 7.2 7.4 7.6 7.8 8. 8.2 8.4
8.6 8.8 9. 9.2 9.4 9.6 9.8 10. 8. 6. 4. 2. ]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[11], line 28
25 plt.clf()
27 plt.scatter(x, y)
---> 28 plt.scatter(x, y_cov)
30 plt.show()
(中略)
File /Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/matplotlib/axes/_axes.py:4578, in Axes.scatter(self, x, y, s, c, marker, cmap, norm, vmin, vmax, alpha, linewidths, edgecolors, plotnonfinite, **kwargs)
4576 y = np.ma.ravel(y)
4577 if x.size != y.size:
-> 4578 raise ValueError("x and y must be the same size")
4580 if s is None:
4581 s = (20 if mpl.rcParams['_internal.classic_mode'] else
4582 mpl.rcParams['lines.markersize'] ** 2.0)
ValueError: x and y must be the same sizeエラーとなってしまいました。
ただこのエラーは「np.convolve」の箇所のエラーではなく、matplotlibでグラフ化する際、Xの値の数とYの値の数が異なることから出てきたエラーです。
つまりモード「full」ではデータの数が変わることが分かります。
再度最初の5点と、最後の5点を計算してみましょう。
最初の5点は「0, 0, 0, 0, 1」=1/5=0.2、「0, 0, 0, 1, 1」=2/5=0.4、「0, 0, 1, 1, 1」=3/5=0.6、「0, 1, 1, 1, 1」=4/5=0.8、「1, 1, 1, 1, 1」=5/5=1という計算が成り立ちます。
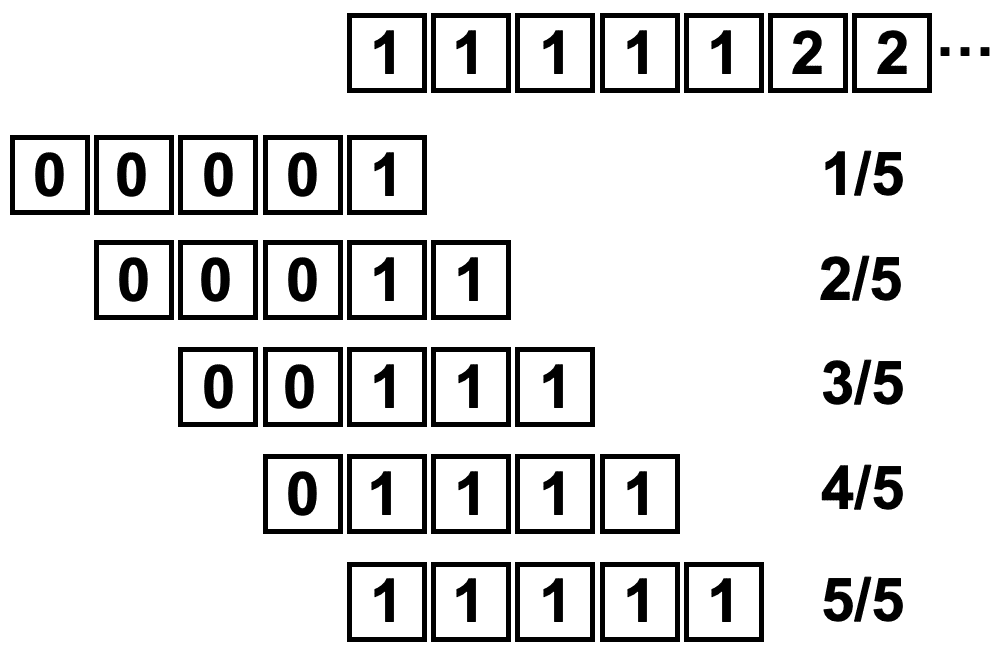
また最後の5点は「10, 10, 10, 10, 10」=50/5=10、「10, 10, 10, 10, 0」=40/5=8、「10, 10, 10, 0, 0」=30/5=6、「10, 10, 0, 0, 0」=20/5=4、「10, 0, 0, 0, 0」=10/5=2という計算が成り立ちます。
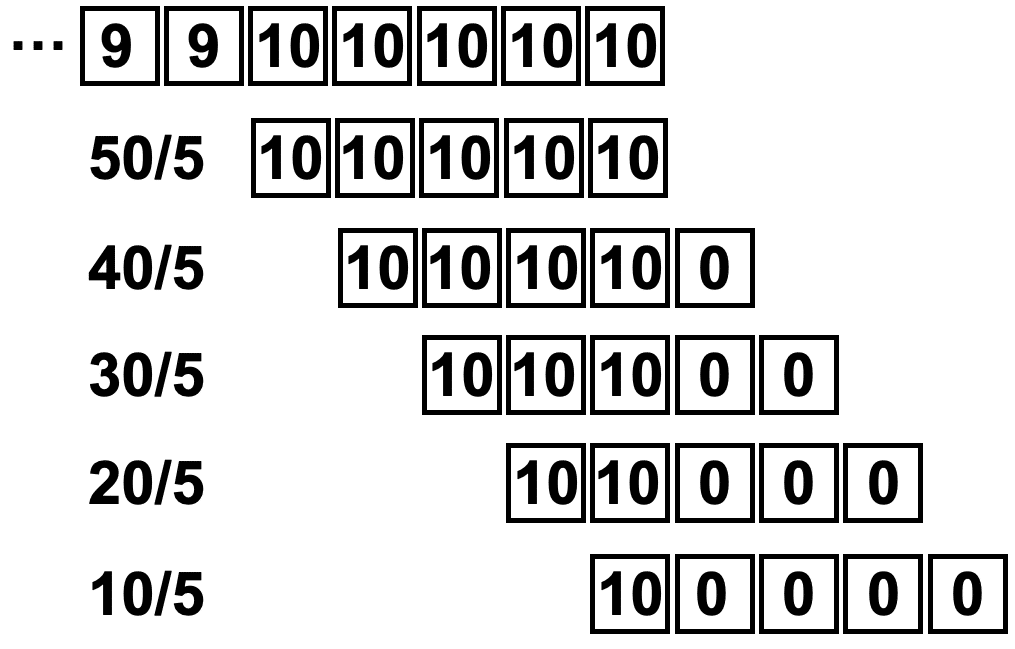
つまりモードが「full」の場合は窓のギリギリにデータの端が入るように配置されるというわけです。
そのためデータの点数が「窓の長さ/2」の整数分だけデータが前後に伸びている形になります。
ということでそれを補正してグラフ化してやるとこんな感じになります。
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
window = 5
#----------この部分を追加----------
data_cutoff = math.floor(window/2)
#----------この部分を追加----------
w = np.ones(window)/window
y_cov = np.convolve(y, w, mode="full")
print(y_cov)
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
#----------この部分を変更----------
plt.scatter(x, y_cov[data_cutoff:-data_cutoff])
#----------この部分を変更----------
plt.show()
実行結果
[ 0.2 0.4 0.6 0.8 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8
3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8 5. 5.2 5.4 5.6
5.8 6. 6.2 6.4 6.6 6.8 7. 7.2 7.4 7.6 7.8 8. 8.2 8.4
8.6 8.8 9. 9.2 9.4 9.6 9.8 10. 8. 6. 4. 2. ]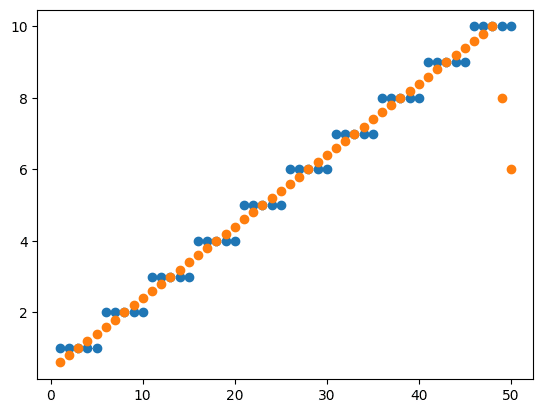
ということで末端を切り落としてみましたが、これなら先ほどの「same」を使えばいいんじゃないかと思います。
valid
最後にvalidです。
こちらもまずは「same」で使ったプログラムでmodeを変えるだけで実行してみましょう。
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
window = 5
w = np.ones(window)/window
#----------この部分を変更----------
y_cov = np.convolve(y, w, mode="valid")
#----------この部分を変更----------
print(y_cov)
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
plt.scatter(x, y_cov)
plt.show()
実行結果
[ 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6
3.8 4. 4.2 4.4 4.6 4.8 5. 5.2 5.4 5.6 5.8 6. 6.2 6.4
6.6 6.8 7. 7.2 7.4 7.6 7.8 8. 8.2 8.4 8.6 8.8 9. 9.2
9.4 9.6 9.8 10. ]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[14], line 28
25 plt.clf()
27 plt.scatter(x, y)
---> 28 plt.scatter(x, y_cov)
30 plt.show()
(中略)
File /Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/matplotlib/axes/_axes.py:4578, in Axes.scatter(self, x, y, s, c, marker, cmap, norm, vmin, vmax, alpha, linewidths, edgecolors, plotnonfinite, **kwargs)
4576 y = np.ma.ravel(y)
4577 if x.size != y.size:
-> 4578 raise ValueError("x and y must be the same size")
4580 if s is None:
4581 s = (20 if mpl.rcParams['_internal.classic_mode'] else
4582 mpl.rcParams['lines.markersize'] ** 2.0)
ValueError: x and y must be the same sizeこちらもmatplotlibでデータ数が合わないというエラーが出てしまいました。
最初の5点を計算してみると「1, 1, 1, 1, 1」=5/5=1、「1, 1, 1, 1, 2」=6/5=1.2、「1, 1, 1, 2, 2」=7/5=1.4、「1, 1, 2, 2, 2」=8/5=1.6、「1, 2, 2, 2, 2」=9/5=1.8という計算が成り立ちます。
最後の5点では「9, 9, 9, 9, 10」=46/5=9.2、「9, 9, 9, 10, 10」=47/5=9.4、「9, 9, 10, 10, 10」=48/5=9.6、「9, 10, 10, 10, 10」=49/5=9.8、「10, 10, 10, 10, 10」=50/5=10となっていることが分かります。
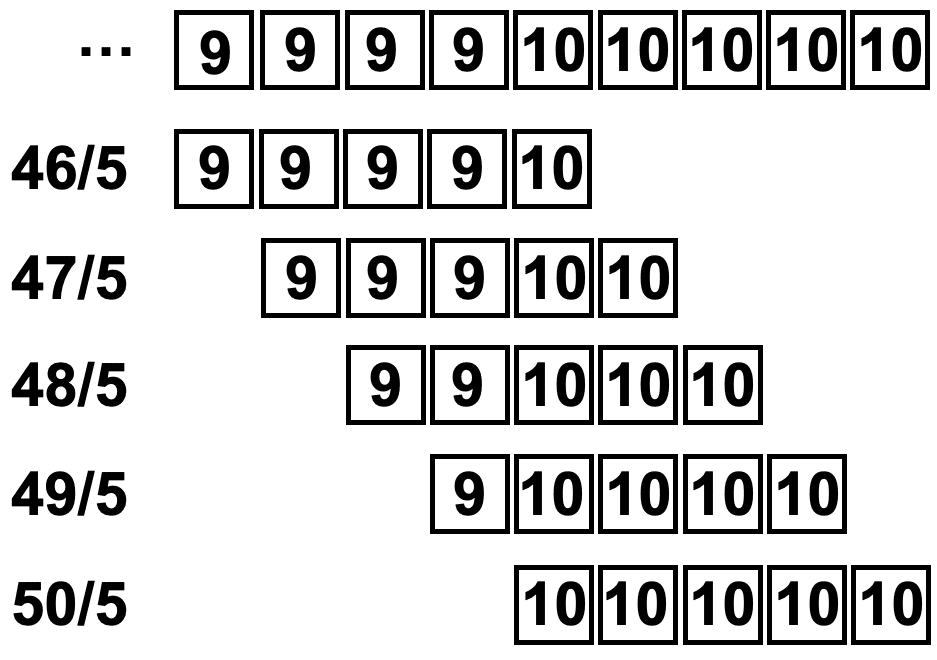
ということで「valid」は窓の末端がデータの末端になるように配置されていることが分かります。
そのためデータの点数は「窓の長さ/2」の整数分だけ両末端が少ない形になります。
そこでグラフ化するにはXの値の両端を切り落としてやる必要があります。
import numpy as np
import math
import matplotlib.pyplot as plt
amount_num = 5
data_points = 50
x = range(1, data_points+1)
y = []
for i in x:
y.append(math.ceil(i/amount_num))
window = 5
#----------この部分を追加----------
data_cutoff = math.floor(window/2)
#----------この部分を追加----------
w = np.ones(window)/window
y_cov = np.convolve(y, w, mode="valid")
print(y_cov)
fig = plt.figure()
plt.clf()
plt.scatter(x, y)
#----------この部分を変更----------
plt.scatter(x[data_cutoff:-data_cutoff], y_cov)
#----------この部分を変更----------
plt.show()
実行結果
[ 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6
3.8 4. 4.2 4.4 4.6 4.8 5. 5.2 5.4 5.6 5.8 6. 6.2 6.4
6.6 6.8 7. 7.2 7.4 7.6 7.8 8. 8.2 8.4 8.6 8.8 9. 9.2
9.4 9.6 9.8 10. ]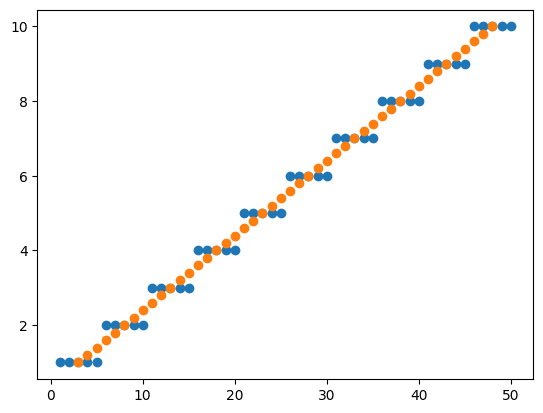
どのモードを使ったとしても末端の値がずれてしまったり、切り落とされたりしているので、とりあえずは「same」を使っておいて、末端はずれていることを念頭に置いておけばいいのではないかなと思います。
次回はNumPyを使って2つのリスト間で1つのリストを条件の判定、その判定結果を使ってもう1つのリストの要素の書き換えをする方法(+Pandasでのやり方)を紹介します。
ではでは今回はこんな感じで。

コメント