Python数値計算ライブラリnumpy
前回、Python数値計算ライブラリnumpyを使って、最大値、最小値、そしてそのインデックスの取得方法を解説しました。

今回は統計でよく用いる数値である平均値、中央値、標準偏差、分散値の取得を行ってみましょう。
今回はnumpyの配列だけで解説していきますので、基本となるプログラムはこんな感じ。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
print(a)配列の数値は前回と同じです。
ということで進めていきましょう。
平均値:np.average、np.mean
まずは一番使うだろう平均値からです。
numpyで平均値を扱う際には「np.average」か「np.mean」を使います。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
print(np.average(a))
print(np.mean(a))
実行結果
4.5
4.5平均値の計算はみなさんご存知の通り、全ての数値を足して、その数で割ると言う方法です。
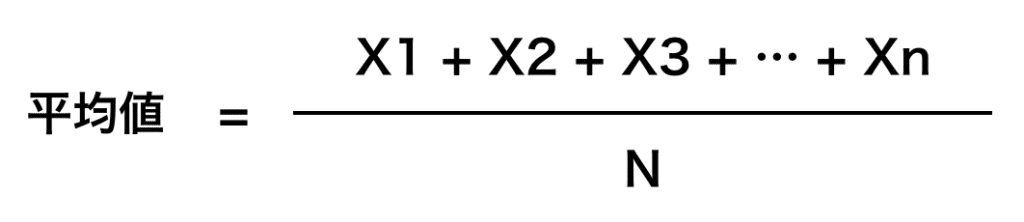
配列には0から9まで10個の数値が含まれますので、平均値が「4.5」というのは正しいです。
では何故numpyには二つの平均値があるのでしょうか?
実は「np.average」を使うと「加重平均」という異なる平均値を計算できるのです。
加重平均とはそれぞれの値に重要度(重み)を設定し、それを踏まえた平均値を計算する方法です。
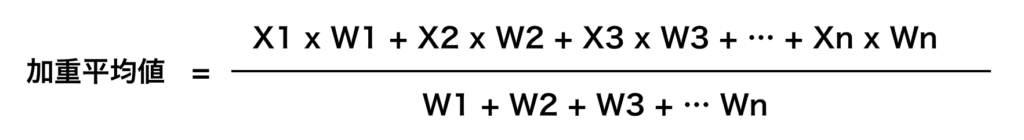
先ほどの配列で前5つの重要度を「1」、後ろ5つの重要度を「2」にして計算してみましょう。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
w = np.array([1, 1, 1, 1, 1, 2, 2, 2, 2, 2])
print(np.average(a, weights=w))
実行結果
5.133333333333334ちなみに「np.average」で重要度を設定しなければ、普通の平均(算術平均といいます)となり、先ほど試した通り「np.mean」と同じ値になります。
中央値:np.median
中央値はデータを順に並べたときに真ん中にある値のことです。
これは先ほどの平均値と比較してみると分かりやすいでしょう。
ということで先ほどの配列で平均値と中央値を計算してみます。
中央値を計算する場合は「np.median」を用います。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
print(np.average(a))
print(np.median(a))
実行結果
4.5
4.5どちらも同じ値になりました。
次に配列の最後に「1000」を追加して、再度計算してみます。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7, 1000])
print(np.average(a))
print(np.median(a))
実行結果
95.0
5.0平均値の場合や先ほど解説した通り、全部の数値を足して、個数で割ることから、一つ大きくずれた数値があると、平均値は大きく変わる傾向にあります。
しかし中央値は「順に並べて、真ん中にくる値」です。
つまり先ほどの配列だと「0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1000」となり、真ん中の「5」が中央値になります。
ちなみに数値の個数が偶数の場合は、中央の二つの数値の平均値になります。
よくニュースで「年収の平均値と中央値では大きな開きがある」なんて言っているのは、このような計算の違いからでてくるわけです。
標準偏差:np.std
次は標準偏差を計算してみましょう。
標準偏差とはデータのばらつきを示す値で、以下の式で計算されます。

ちなみに「A」は配列の数値の平均値です。
ということでnumpyで計算してみるとこんな感じになります。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
print(np.std(a))
実行結果
2.8722813232690143個人的にはデータのエラーバーなんかを表示するのに用いています。
分散値:np.var
最後は分散値です。
分散値の計算方法は標準偏差と似ていて、こんな感じです。

ということでnumpyで計算してみましょう。
import numpy as np
a = np.array([1, 5, 3, 4, 0, 9, 6, 2, 8, 7])
print(np.var(a))
実行結果
8.25ちなみに分散値の平方根は標準偏差となります。
√8.25 を計算してみると、確かに2.8722813232690143となり、標準偏差と分散値の関係性が正しいことがわかります。
今回はnumpyで統計値の計算方法を解説してみました。
平均値と標準偏差はデータを解析するのによく使う人もいるのではないでしょうか。
次回はnumpyではなく、他のライブラリを使って平均値や標準偏差などの計算を解説していきたいと思います。

ということで今回はこんな感じで。

コメント