numpyとstatisticsで値が違う?
前回、前々回と数値計算ライブラリnumpyと数理統計ライブラリstatisticsを使って、平均値、中央値、標準偏差、分散値の計算を紹介しました。


しかしその際、numpyの標準偏差np.stdと分散値np.varの値が、statisticsの標準偏差stdevと分散値varianceの値と異なっているということを見つけました。
今回はそれが何故起こったのかを考えていきたいと思います。
まずは基本となるプログラムから。
今回はnumpyもstatisticsも使うので両方インポートしますが、statisticsを何度もタイプするのは疲れるので、「stat」としてインポートします。
import numpy as np
import statistics as stat
a = [1, 5, 3, 4, 0, 9, 6, 2, 8, 7]
print("<Standard Deviation>")
print(np.std(a))
print(stat.stdev(a))
print("<Variance>")
print(np.var(a))
print(stat.variance(a))
実行結果
<Standard Deviation>
2.8722813232690143
3.0276503540974917
<Variance>
8.25
9.166666666666666確かに標準偏差も分散値も異なっています。
pstdevとpvariance
実はstatisticsの標準偏差と分散にはもう一つの計算方法があります。
それが「pstdev」と「pvariance」です。
これらは母集団の標準偏差と分散を計算するコマンドです。
ちなみに前に紹介した「stdev」は不偏標準偏差、「variance」は不偏分散という値になります。
とりあえず計算してみましょう。
import numpy as np
import statistics as stat
a = [1, 5, 3, 4, 0, 9, 6, 2, 8, 7]
print("<Standard Deviation>")
print(np.std(a))
print(stat.pstdev(a))
print("<Variance>")
print(np.var(a))
print(stat.pvariance(a))
実行結果
<Standard Deviation>
2.8722813232690143
2.8722813232690143
<Variance>
8.25
8.25同じ値になりました。
ということはnumpyの「np.std」と「np.var」はstatisticsの「pstdev」 と「pvariance」と同じ計算をしていると言えそうです。
ではstatisticsの「stdev」と「pstdev」、また「variance」と「pvariance」はどう違うのでしょうか?
標本と母集団
これには少し統計のことを勉強する必要があります。
私自身も統計をしっかり学んだわけではないので、間違っていたらごめんなさい。
まず統計ではものすごく数多くのデータ、もしくはすべてのデータ値がわかっているわけではない「母集団」が存在します。
そして全部を計算するのは大変だったり、もしくは全部を計算できない場合、そこからいくつかのデータを抽出し、統計処理をし、母集団の統計値を推定します。
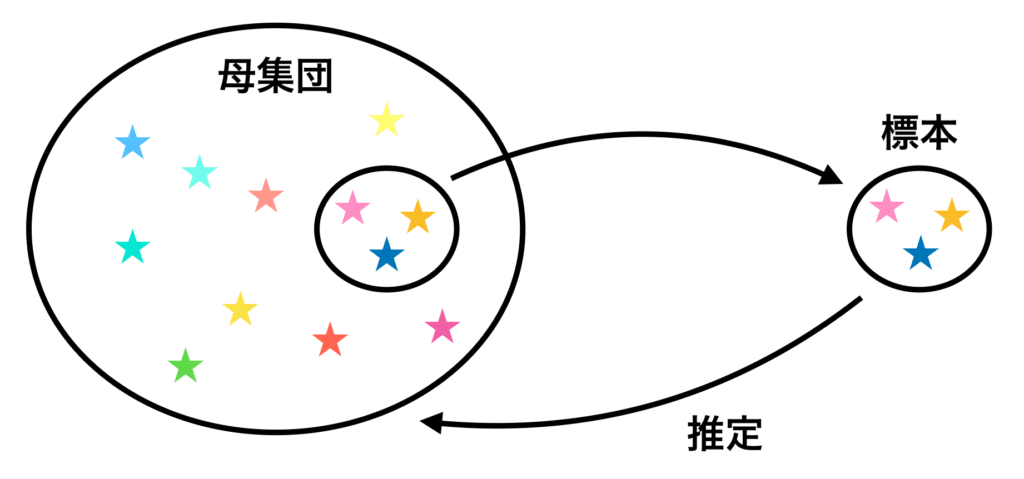
ということは標準偏差も分散値も、「母集団に対する標準偏差・分散値」と「標本に対する標準偏差・分散値」が存在するわけです。
これで少し明らかになってきました。
numpyの「np.std」、「np.var」、そしてstatisticsの「pstdev」、「pvariance」は母集団に対する標準偏差、分散値を計算するコマンドなのです。
またstatisticsの「stdev」と「variance」は標本に対する標準偏差と分散値を計算するコマンドになるということです。
ちなみにそれぞれを計算式にするとこんな感じになります。
・母集団に対する標準偏差

・母集団に対する分散値

・標本に対する標準偏差
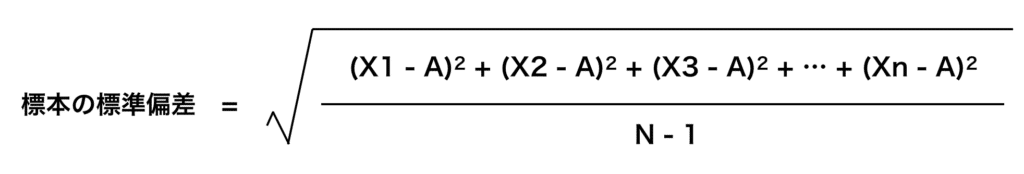
・標本に対する分散値
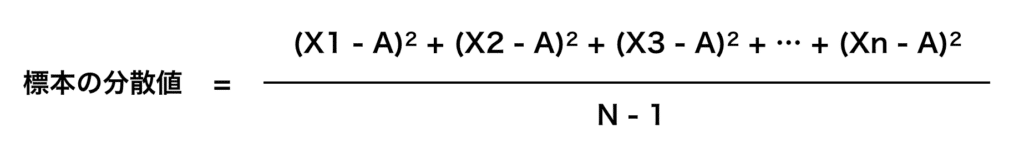
違うところはそう、分母が「N(データの個数)」になっているか「N – 1(データの個数 – 1)」となっているかです。
これは標本だとデータ数が少なるなることから、計算値が小さい方に偏りやすいということで補正をしているということらしいです。
こちらのウェブサイトで詳しく解説されていますので、もし良かったら見てみてください。
今回はnumpyとstatisticsの標準偏差、分散値に関して解説をしました。
最終的にはたった「-1」 をしているかしていないかだけの違いですが、統計にとってはこの差が違う目的で用いる重要な違いだったりします。
個人的にはこういう本質的な違いというのを理解して使っていくというのが重要だなぁと思った記事でした。
ということで今回はこんな感じで。

コメント