NumPy
前回、NumPyで配列を繰り返し並べ、タイル状にするnp.tileを紹介しました。
今回はNumPyでπや角度とラジアンの変換、三角関数(sin、cos、tan)、逆三角関数(arcsin、arccos、arctan)の計算方法を紹介します。
それでは始めていきましょう。
πの値の取得方法
NumPyでπの値を取得するには「np.pi」を用います。
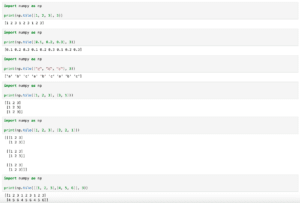
import numpy as np
print(np.pi)
実行結果
3.141592653589793角度とラジアンの変換
角度をラジアンに変換するには「np.radians(角度)」を、ラジアンを角度に変換するには「np.degrees(ラジアン)」を用います。
import numpy as np
deg = 180
print(np.radians(deg))
rad = 2*np.pi
print(np.degrees(rad))
実行結果
3.141592653589793
360.0ちなみに数式を自作する場合は角度からラジアンに変換するには「角度x2π/360」で、ラジアンから角度に変換するには「ラジアンx360/2π」です。
import numpy as np
deg = 180
print(deg*2*np.pi/360)
rad = 2*np.pi
print(rad*360/(2*np.pi))
実行結果
3.141592653589793
360.0またnp.degrees、np.radiansの場合は複数の要素を含んだndarrayを与えると一度に変換してくれます。
import numpy as np
degs = [0, 90, 180, 270, 360]
print(np.radians(degs))
rads = [0*2*np.pi/360, 90*2*np.pi/360, 180*2*np.pi/360, 270*2*np.pi/360, 360*2*np.pi/360]
print(np.degrees(rads))
実行結果
[0. 1.57079633 3.14159265 4.71238898 6.28318531]
[ 0. 90. 180. 270. 360.]三角関数
三角関数を計算するにはそれぞれ「np.sin(ラジアン)」、「np.cos(ラジアン)」、「np.tan(ラジアン)」とします。
ここで注意すべき点は引数で与えるのは「ラジアン」であり、「角度」ではないことです。
つまりこの様に初期値が角度の場合、そのまま与えると間違った答えとなってしまいます。
import numpy as np
degs = [0, 45, 90]
print(np.sin(degs))
実行結果
[0. 0.85090352 0.89399666]つまりnp.sin()に入れる前に「np.radians(角度)」でラジアンに変換してから、np.sinに入れる必要があるということです。
import numpy as np
degs = [0, 45, 90]
print(np.sin(np.radians(degs)))
実行結果
[0. 0.70710678 1. ]cos、tanも試してみるとこんな感じになります。
import numpy as np
degs = [0, 45, 90]
print(np.sin(np.radians(degs)))
print(np.cos(np.radians(degs)))
print(np.tan(np.radians(degs)))
実行結果
[0. 0.70710678 1. ]
[1.00000000e+00 7.07106781e-01 6.12323400e-17]
[0.00000000e+00 1.00000000e+00 1.63312394e+16]ちなみにそれぞれグラフで表示するとこんな感じになります。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 360*5)
sin_y = np.sin(np.radians(x))
cos_y = np.cos(np.radians(x))
fig = plt.figure()
plt.clf()
plt.plot(x, sin_y, label="sin")
plt.plot(x, cos_y, label="cos")
plt.xlabel("degrees")
plt.legend()
plt.show()
実行結果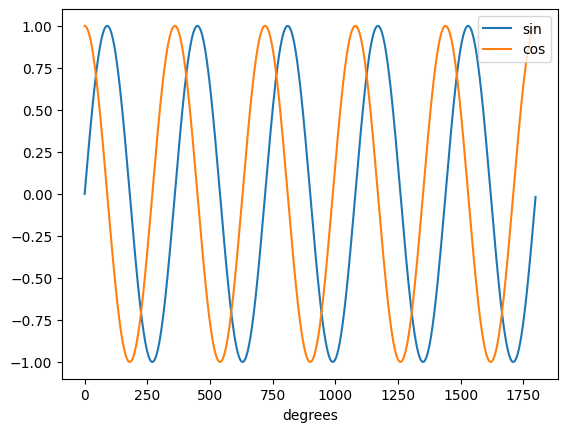
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 90)
tan_y = np.tan(np.radians(x))
fig = plt.figure()
plt.clf()
plt.plot(x, tan_y, label="tan")
plt.xlabel("degrees")
plt.legend()
plt.show()
実行結果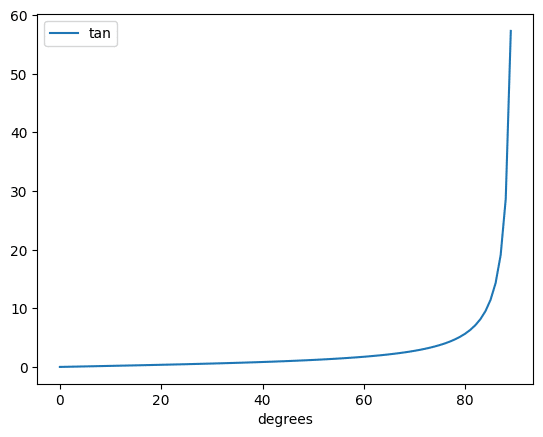
逆三角関数
逆三角関数を計算する場合はそれぞれ「np.arcsin(値)」、「np.arccos(値)」、「np.arctan(値)」を用います。
またこの場合、結果はラジアンで得られるので角度に直したい場合は「np.degrees()」を用い、変換します。
import numpy as np
degs = [0, 45, 90]
sin_vals = np.sin(np.radians(degs))
cos_vals = np.cos(np.radians(degs))
tan_vals = np.tan(np.radians(degs))
print(np.degrees(np.arcsin(sin_vals)))
print(np.degrees(np.arccos(cos_vals)))
print(np.degrees(np.arctan(tan_vals)))
実行結果
[ 0. 45. 90.]
[ 0. 45. 90.]
[ 0. 45. 90.]次回はSciPyのfftを使ってフーリエ変換する方法を紹介します。
ではでは今回はこんな感じで。

コメント