ランダムな波形
前回、SciPyでデータを補完(interpolation)する方法を紹介しました。

今回はPythonでランダムな波形を作成する方法を紹介します。
なんでこんなことをしようと思ったかと言うと、周波数解析を勉強しようと思ったのですが、良い波形サンプルがないということでそれならばランダムな波形を作ればいいじゃんと思ったのがきっかけです。
そしてなぜ周波数解析をしようと思ったかと言うと、最近脳波に興味があり、その周波数解析をしたいからというわけです。
そのため今回はランダムな波形を作成する方法を紹介しますが、将来的には脳波に類似した波形を作成するプログラムが作れたらなぁなんて思っています。
そこまではできるかどうかは分かりませんが、とりあえず今回はランダムな波形を作るプログラムを紹介していきます。
それでは始めていきましょう。
横軸が角度(ラジアン)のsin波
sin波ができれば位相が違うだけのcos波も作れると言うことで、sin波を使っていきます。
ということでまずはこれまで何度か出てきた横軸が角度(ラジアン)のsin波です。
sinに関してはnumpyを使って「np.sin(ラジアン)」でsinの値を取得します。
そして度数の角度をラジアンに変換するには「\(角度\times\frac{\pi}{180}\)」です。
そしてさらに360°までの間のピークの数を増やすために「n倍(nはピークの数)」しています。
ということでこんな感じ。
import matplotlib.pyplot as plt
import numpy as np
n = 3
x = range(0, 360)
y = [np.sin(i*np.pi/180*n) for i in x]
plt.plot(x,y)
plt.grid()
plt.show()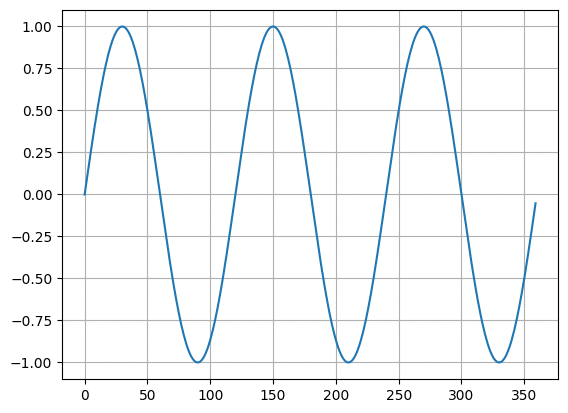
横軸が時間のsin波
次に時間に対する周波数解析ができるよう横軸が時間のsin波を作成していきます。
最終的に脳波のようなデータを作りたいので、実際のデータを模した形でのデータを作成していきます。
実際のデータの時間軸において一定時間内(1秒)の点の数はサンプリングレートであり、点と点の間の時間差は「\(\frac{1}{サンプリングレート}\)」で表されます。
また周波数[Hz]は1秒間の波の数(何回振幅したか)であり、1秒間の振幅数は「\(2\pi\times Hz\)」(角周波数の式)で表されます。
そして特定の時間における波の高さを計算するには「\(2\pi\times Hz\times sec\)」で表すことができます。
と言うことでこんな感じ。
import matplotlib.pyplot as plt
import numpy as np
time = 60
samplingrate = 1000
hz_range = [10]
time_list = np.arange(0, time, 1/samplingrate)
for hz in hz_range:
y = np.sin(2*np.pi*hz*time_list)
plt.plot(x,y)
plt.grid()
plt.xlim(0, 1)
plt.show()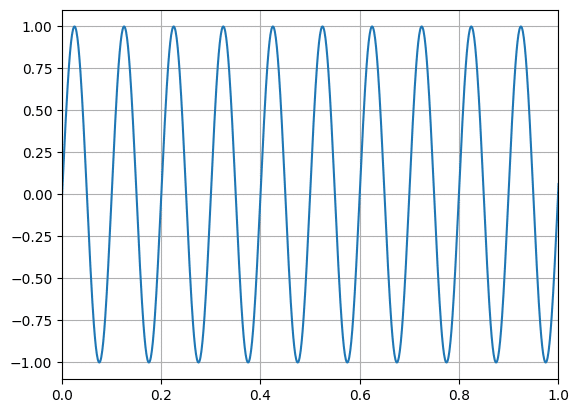
周波数が10 Hzなので1秒間に10回振幅する波ができました。
ちなみに「hz_range」と周波数をリスト化しているのは、これから複数の異なる波長の波を作成するためです。
波の合成
次に波の合成をしていきます。
波の合成は特に難しいことはなく、複数の周波数のデータを作成し、それらの同じ時間の値を足し算するだけです。
ただここで足し算する際にPandasを使うと楽なので、Pandasを使った書き方に変更しています。
まずは10 Hz、11 Hz、12 Hzの3つの波を作成し表示してみます。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
time = 60
samplingrate = 1000
hz_range = [10,11,12]
df = pd.DataFrame()
df["Time"] = np.arange(0, time, 1/samplingrate)
for hz in hz_range:
df[hz] = np.sin(2*np.pi*hz*df["Time"])
fig = plt.figure()
for name in df.columns[1:]:
plt.plot(df["Time"], df[name], label=f"{name} Hz")
plt.grid()
plt.legend()
plt.xlim(0, 1)
plt.show()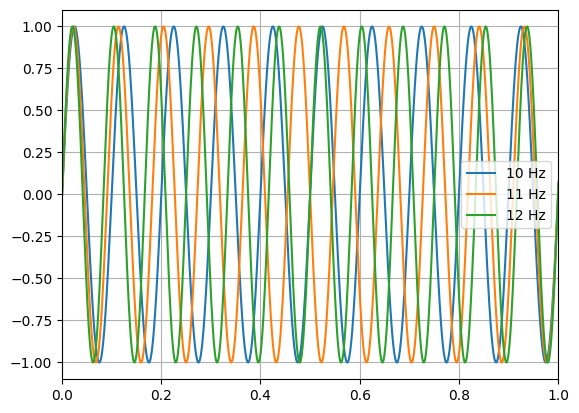
Pandasのデータフレームを作成し、時間軸である「Time」の列を追加したのち、各周波数のデータを列として追加しています。
つまりデータはデータフレームにこんな感じで格納されています。
Time 10 11 12
0 0.000 0.000000 0.000000 0.000000
1 0.001 0.062791 0.069060 0.075327
2 0.002 0.125333 0.137790 0.150226
3 0.003 0.187381 0.205863 0.224271
4 0.004 0.248690 0.272952 0.297042
... ... ... ... ...
59995 59.995 -0.309017 -0.338738 -0.368125
59996 59.996 -0.248690 -0.272952 -0.297042
59997 59.997 -0.187381 -0.205863 -0.224271
59998 59.998 -0.125333 -0.137790 -0.150226
59999 59.999 -0.062791 -0.069060 -0.075327次に波の合成を行うため、時間軸である「Time」以外の列の同じ時間のデータを足し算します。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
time = 60
samplingrate = 1000
hz_range = [10,11,12]
df = pd.DataFrame()
df["Time"] = np.arange(0, time, 1/samplingrate)
for hz in hz_range:
df[hz] = np.sin(2*np.pi*hz*df["Time"])
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlim(0, 10)
plt.show()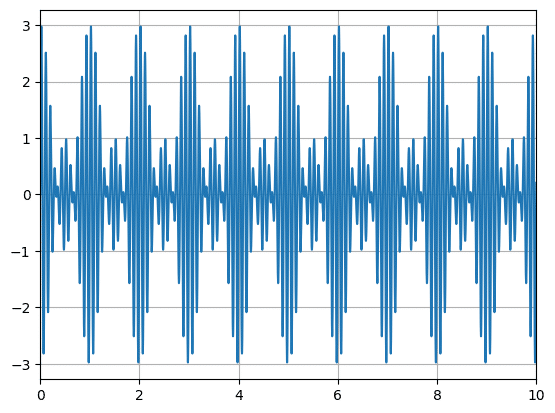
「df.iloc[:, 1:]」で1列目を除いたすべてのデータを取得し、「.sum(axis=1)」で横方向に足し算をしています。
先ほどの3つの波では同じ振幅になっているので、波によって振幅を変化させられるようにします。
周波数に対応するように「波の振幅のリスト」を作成します。
ちなみに今回は振幅の大きさを数値で設定もできるし、ランダムに設定することができるようにもしてみました。
数値を設定すればその振幅の大きさは設定した値の倍数に、「0」とした場合は0から1までの間でランダムに倍数が設定されます。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = [10,11,12]
hz_weight = [1, 0.1, 0]
df = pd.DataFrame()
df["Time"] = np.arange(0, time, 1/samplingrate)
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
df[hz] = weight * np.sin(2*np.pi*hz*df["Time"])
fig = plt.figure()
for name in df.columns[1:]:
plt.plot(df["Time"], df[name], label=f"{name} Hz")
plt.grid()
plt.legend()
plt.xlim(0, 1)
plt.show()
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlim(0, 10)
plt.show()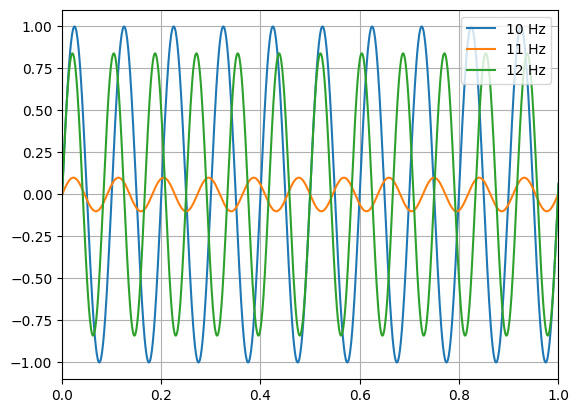
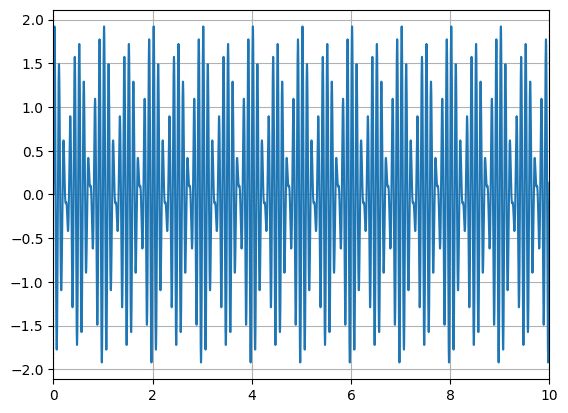
このままでは3つの波の位相が揃っているので、位相をランダムに変化するようにします。
位相を変えるには「np.sin(2*np.pi*hz*df[“Time”])」の括弧内に変化させるだけの角度をラジアンで追加します。
ということでこんな感じ。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = [10,11,12]
hz_weight = [1, 0.1, 0]
df = pd.DataFrame()
df["Time"] = np.arange(0, time, 1/samplingrate)
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
df[hz] = weight * np.sin(2*np.pi*hz*df["Time"] + fai)
fig = plt.figure()
for name in df.columns[1:]:
plt.plot(df["Time"], df[name], label=f"{name} Hz")
plt.grid()
plt.legend()
plt.xlim(0, 1)
plt.show()
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlim(0, 10)
plt.show()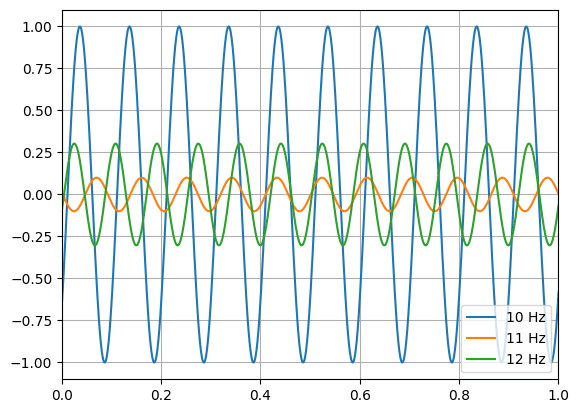
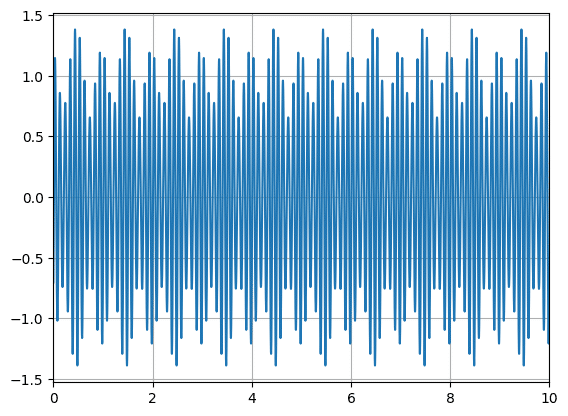
次に3つの波ではなく、さらに大量の波を合成するため、周波数のリストを「np.arange」で作成し、振幅の大きさのリストをすべてランダムとしてみました。
ちなみに周波数のリストは「0から40 Hzまでで0.1 Hz刻み」としています。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight = [0 for _ in hz_range]
df = pd.DataFrame()
df["Time"] = np.arange(0, time, 1/samplingrate)
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
df[hz] = weight * np.sin(2*np.pi*hz*df["Time"] + fai)
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlim(0, 10)
plt.show()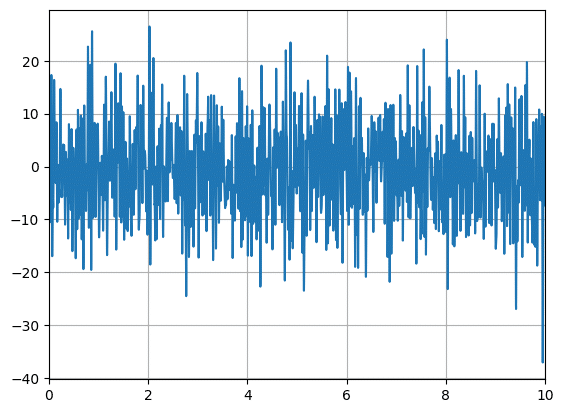
かなりランダムな波を作成することができました。
ただしPandasで列を一つずつ大量に追加していくとこんな警告が出ることがあります。
PerformanceWarning: DataFrame is highly fragmented. This is usually the result of calling
`frame.insert` many times, which has poor performance. Consider joining all columns at once
using pd.concat(axis=1) instead. To get a de-fragmented frame, use `newframe = frame.copy()`簡単に言うと「データフレームにちまちまデータを追加するな。一気に入れろ。」という感じでしょうか。
ということで時間と各波長の時間に対するデータは一度リストに格納しておいて、格納し終わったらデータフレームに入れるという方式に変えてみたところ、先ほどの警告は出なくなりました。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.5)
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlim(0, 10)
plt.show()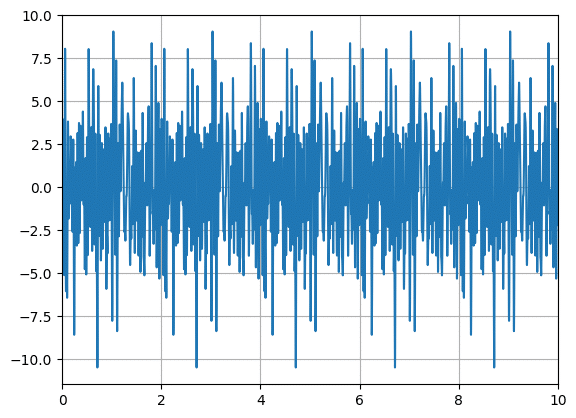
最後にX軸とY軸のラベルを追加しておきます。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.5)
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()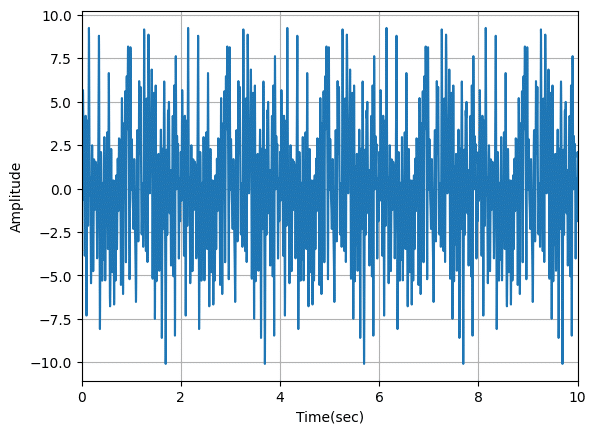
次回はこの波をFFT(高速フーリエ変換)し、周波数解析をしてみましょう。
ではでは今回はこんな感じで。

コメント