目次
再帰処理
前回、Pythonで再帰処理を使って面積を指定したガウス分布を作成する方法を紹介しました。
あわせて読みたい
【Python基礎】再帰処理を使って面積を指定したガウス分布を作成する方法
再帰処理 前回、PythonのMatplotlibでadd_subplotを使って複数のグラフを一括で表示する方法を紹介しました。 今回は再帰処理を使って面積を指定したガウス分布を作成す…
今回は前回の再帰処理を使って、再帰処理の回数を大幅に減らす方法を紹介します。
ちなみに前回の再帰処理のプログラムを少し変えて、経過を表示するようにしたプログラムがこちらです。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
n = 10000
target = 500
delta = 0.01
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
def target_area(n, x_list, a, m, s, target, delta, i=0):
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
print(i, a, y_area)
if n == 0:
return "no answer..."
elif y_area <= target:
return a
new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
return new_a
new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
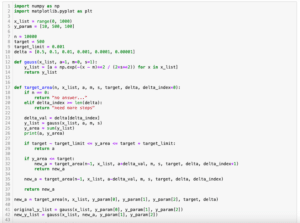
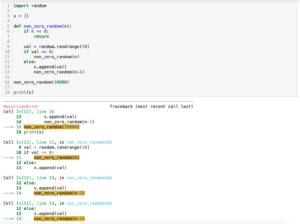
original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
y_area = sum(new_y_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, original_y_list)
plt.plot(x_list, new_y_list)
plt.show()
実行結果
0 10 2506.6268372625827
1 9.99 2504.1202104253234
2 9.98 2501.613583588058
3 9.97 2499.1069567507966
4 9.96 2496.600329913535
5 9.950000000000001 2494.0937030762716
（中略）
797 2.03000000000017 508.8452479643479
798 2.02000000000017 506.3386211270855
799 2.0100000000001703 503.8319942898231
800 2.0000000000001705 501.32536745256067
801 1.9900000000001705 498.818740615298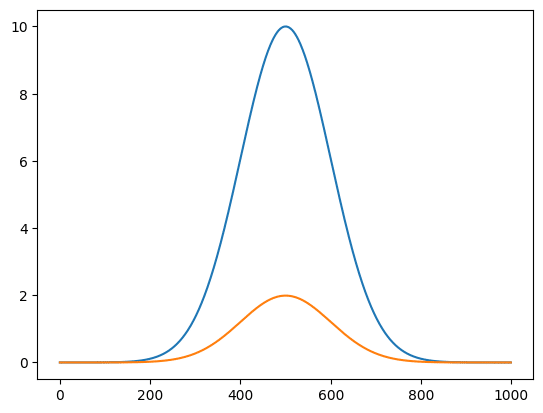
deltaを0.01としたときは約800回程度の再帰処理が行われて答えが出ています。
さらにdeltaを0.001とすると再帰処理の上限を超えてしまい、処理が強制終了されてしまいます。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
n = 10000
target = 500
delta = 0.001
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
def target_area(n, x_list, a, m, s, target, delta, i=0):
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
print(i, a, y_area)
if n == 0:
return "no answer..."
elif y_area <= target:
return a
new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
return new_a
new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
y_area = sum(new_y_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, original_y_list)
plt.plot(x_list, new_y_list)
plt.show()
実行結果
0 10 2506.6268372625827
1 9.999 2506.3761745788643
2 9.998000000000001 2506.125511895136
（中略）
2966 7.034000000000786 1763.161317330699
2967 7.0330000000007855 1762.9106546469782
2968 7.032000000000785 1762.6599919632508
---------------------------------------------------------------------------
RecursionError Traceback (most recent call last)
Cell In[10], line 28
25 new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
26 return new_a
---> 28 new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
30 original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
31 new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
Cell In[10], line 25, in target_area(n, x_list, a, m, s, target, delta, i)
22 elif y_area <= target:
23 return a
---> 25 new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
26 return new_a
Cell In[10], line 25, in target_area(n, x_list, a, m, s, target, delta, i)
22 elif y_area <= target:
23 return a
---> 25 new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
26 return new_a
[... skipping similar frames: target_area at line 25 (2966 times)]
Cell In[10], line 25, in target_area(n, x_list, a, m, s, target, delta, i)
22 elif y_area <= target:
23 return a
---> 25 new_a = target_area(n-1, x_list, a-delta, m, s, target, delta, i=i+1)
26 return new_a
Cell In[10], line 19, in target_area(n, x_list, a, m, s, target, delta, i)
17 y_list = gauss(x_list, a, m, s)
18 y_area = sum(y_list)
---> 19 print(i, a, y_area)
20 if n == 0:
21 return "no answer..."
File /Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/ipykernel/iostream.py:635, in OutStream.write(self, string)
633 raise ValueError(msg)
634 else:
--> 635 is_child = not self._is_master_process()
636 # only touch the buffer in the IO thread to avoid races
637 with self._buffer_lock:
File /Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/ipykernel/iostream.py:506, in OutStream._is_master_process(self)
505 def _is_master_process(self):
--> 506 return os.getpid() == self._master_pid
RecursionError: maximum recursion depth exceeded while calling a
Python objectこの様な場合、再帰処理の上限回数を上げるというのが一つの手で、その方法は前に紹介していますので、よかったらこちらの記事をどうぞ。
あわせて読みたい
【Python基礎】再帰処理を大量に行った場合に出る「RecursionError: maximum recursion depth exceeded …
再帰処理 前回は、Pythonで再帰処理を使って0を含まないランダムな数値のリストを作成する方法を紹介しました。 今回は再帰処理を大量に行った場合に出る「RecursionErr…
ただし再帰処理の上限回数を上げるということは力技でコストを掛けて解を見つけるということであまりCPUに優しい方法ではありません。
そこで今回の様に目標となる値がある場合、再帰処理の回数を減らす様なプログラムにするのが良いと考えられます。
ということで今回はその方法を紹介します。
それでは始めていきましょう。
再帰処理の回数を減らす方法
再帰処理の回数を減らすにはどういう処理をしたいかによって方針が異なると思いますが、今回の場合、再帰処理のたびに変数「delta」の分だけパラメータが減らされていって、指定した面積を下回るかを検討します。
つまりdeltaが小さければ小さいほど、再帰処理の回数が多くなるというわけです。
しかしながら最初の方は小さなdeltaで削っていっても、指定した面積にたどり着くことがないので、処理としてはほぼ無駄なわけです。
ということでdeltaを変動性にして、まずは大きなdeltaを使ってざっくりと値を削っていく、そして指定した面積を下回ったところで値を一度戻して、再度少し小さくしたdeltaで値を削っていくを繰り返します。
これにより無駄なところでちまちまとパラメータを減らしていく無駄が大幅に削減されます。
作成したプログラムはこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
n = 10000
target = 500
target_limit = 0.001
delta = [0.5, 0.1, 0.01, 0.001, 0.0001, 0.00001]
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
def target_area(n, x_list, a, m, s, target, delta, delta_index=0, i=0):
if n == 0:
return "no answer..."
elif delta_index >= len(delta):
return "need more steps"
delta_val = delta[delta_index]
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
print(i, a, y_area)
if target - target_limit <= y_area <= target + target_limit:
return a
if y_area <= target:
new_a = target_area(n-1, x_list, a+delta_val, m, s, target, delta, delta_index+1, i=i+1)
return new_a
new_a = target_area(n-1, x_list, a-delta_val, m, s, target, delta, delta_index, i=i+1)
return new_a
new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
y_area = sum(new_y_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, original_y_list)
plt.plot(x_list, new_y_list)
plt.show()変わったところとしては新たに「target_limit」という変数ができたことと、「delta」がリストになったことです。
target_limit = 0.001
delta = [0.5, 0.1, 0.01, 0.001, 0.0001, 0.00001]target_limitは目標値であるtargetと合わせて「target±target_limit」の値になったときに処理が終了するための条件分岐に使います。
if target - target_limit <= y_area <= target + target_limit:
return aまた処理が終了するための条件に引っ掛からず、目標値よりも小さくなった場合、パラメータ「a」の値を戻しつつ、deltaのリストの要素を次の要素（より小さなdelta）へと移動するようにします。
if y_area <= target:
new_a = target_area(n-1, x_list, a+delta_val, m, s, target, delta, delta_index+1, i=i+1)
return new_a実際使ってみましょう。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
n = 10000
target = 500
target_limit = 0.001
delta = [0.5, 0.1, 0.01, 0.001, 0.0001, 0.00001]
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
def target_area(n, x_list, a, m, s, target, delta, delta_index=0, i=0):
if n == 0:
return "no answer..."
elif delta_index >= len(delta):
return "need more steps"
delta_val = delta[delta_index]
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
print(i, a, y_area)
if target - target_limit <= y_area <= target + target_limit:
return a
if y_area <= target:
new_a = target_area(n-1, x_list, a+delta_val, m, s, target, delta, delta_index+1, i=i+1)
return new_a
new_a = target_area(n-1, x_list, a-delta_val, m, s, target, delta, delta_index, i=i+1)
return new_a
new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
y_area = sum(new_y_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, original_y_list)
plt.plot(x_list, new_y_list)
plt.show()
実行結果
0 10 2506.6268372625827
1 9.5 2381.2954953994563
2 9.0 2255.9641535363276
3 8.5 2130.632811673203
4 8.0 2005.3014698100712
（中略）
38 1.9947500000000002 500.00938836295495
39 1.9947400000000002 500.0068817361169
40 1.9947300000000001 500.00437510928
41 1.99472 500.0018684824427
42 1.99471 499.99936185560557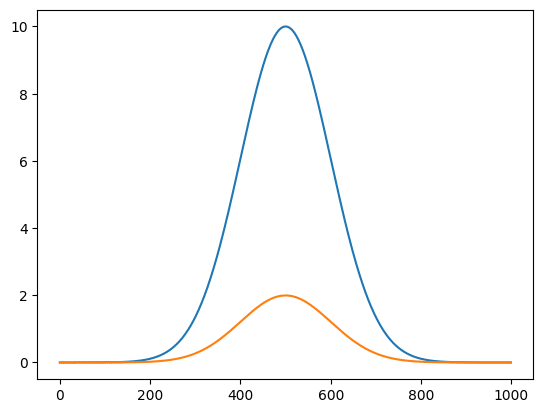
先ほどはdeltaが0.01で800回ほど繰り返されていた処理が、最小のdeltaが0.00001にもかかわらず40回ほどの処理で済んでいます。
ということでもちろん力技でやるべきところもあるでしょうが、大量の処理をする必要ができた際は一度立ち止まって処理により負荷を低減できないか考えてみることも必要かなと思います。
次回は再帰処理でちょっと楽しみができる金利計算を試してみたのでそのプログラムを紹介します。
ではでは今回はこんな感じで。
コメント