SciPy
前回、RDkitでデータベースから化合物の構造情報を取得し描画する方法を紹介しました。
今回はSciPyのintegrate.quadを使って積分する方法を紹介します。
それでは始めていきましょう。
integrate.quadで定積分をする方法
SciPyのintegrate.quadで定積分をするにはまずは式を関数として準備します。
今回は一次関数「y = 2x」を例に使ってみます。
グラフを描いてみるとこんな感じです。
import matplotlib.pyplot as plt
x_list = range(0, 10)
def equation(x):
y = 2 * x
return y
y_list = [equation(x) for x in x_list]
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.show()
実行結果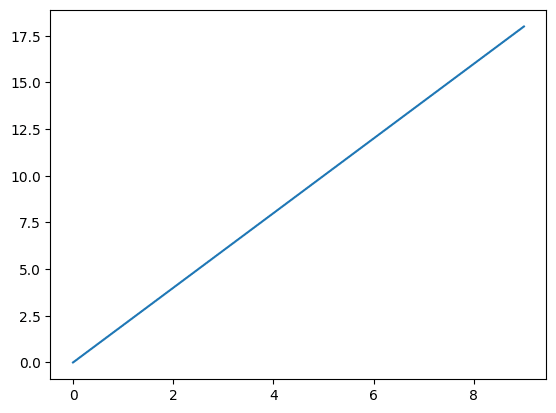
準備する式で重要なのは単純に変数に数字を入れたら、数字が返ってくる式を作ることです。
def equation(x):
y = 2 * x
return y関数を作るとなると利便性を考えて、リストを入れて、計算結果のリストが返ってくる関数としてしまうこともあるかもしれませんが、それではintegrate.quadを使用できません。
つまりこういう関数ではダメということです。
def equation(x_list):
y_list = [2 * x for x in x_list]
return y_listそれでは実際にintegrate.quadを使ってみましょう。
integrate.quadを使うにはまずインポートします。
from scipy.integrate import quadそして「quad(式, 値1, 値2)」とします。
range関数と違って、値2は範囲に入りますので注意してください。
from scipy.integrate import quad
def equation(x):
y = 2 * x
return y
area = quad(equation, 0, 9)
print(area)
実行結果
(81.0, 8.992806499463768e-13)タプルで2つの値が返ってきますが、1つ目が積分値、2つ目が誤差です。
一次関数の場合、積分値、つまり囲まれた領域の面積は台形の公式で計算することができます。
import matplotlib.pyplot as plt
x_list = range(0, 10)
def equation(x):
y = 2 * x
return y
y_list = [equation(x) for x in x_list]
area = (y_list[0] + y_list[-1])*(x_list[-1] - x_list[0])/2
print(area)
実行結果
81.0先ほど少し出てきた様にrange関数では最後の数値を含まない範囲であるため、range(0, 10)がquad(equation, 0, 9)に相当します。
定数が変えられる式
次に定数が変更できる式の場合を見てみましょう。
例えば次に示すガウス関数では「a」、「m」、「s」が定数ですが、変更可能になっています。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 100)
y_param = [5, 50, 10]
def gauss(x, a=1, m=0, s=1):
y = a * np.exp(-(x - m)**2 / (2*s**2))
return y
y_list = [gauss(x, y_param[0], y_param[1], y_param[2]) for x in x_list]
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.show()
実行結果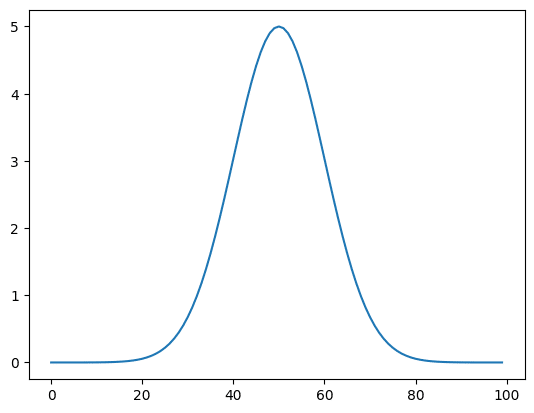
「x」が変数ですが、他の定数を与える場合は「args=(a, b, c)」を追加します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
x_list = range(0, 100)
y_param = [5, 50, 10]
def gauss(x, a, m, s):
y = a * np.exp(-(x - m)**2 / (2*s**2))
return y
area = quad(gauss, 0, 100, args=(y_param[0], y_param[1], y_param[2]))
print(area)
実行結果
(125.33134187865653, 1.0864129507126563e-07)次回はmatplotlibのpcolormeshのカラーバーの範囲を設定する方法と正規化(ノーマライズ)する方法を紹介します。
ではでは今回はこんな感じで。

コメント