SciPy
前回、NumPyでπや角度とラジアンの変換、三角関数(sin、cos、tan)、逆三角関数(arcsin、arccos、arctan)の計算方法を紹介しました。
SciPyのscipy.fftによる高速フーリエ変換の仕方を紹介します。
ちなみにNumPyを使って高速フーリエ変換する方法はこちらの記事で紹介していますので、良かったらどうぞ。
今回高速フーリエ変換するデータとして20 Hzのsin波のデータを準備しました。
import numpy as np
import matplotlib.pyplot as plt
time = np.arange(0, 1, 0.001)
y = np.sin(20*2*np.pi*time)
fig = plt.figure()
plt.clf()
plt.plot(time, y)
plt.show()
実行結果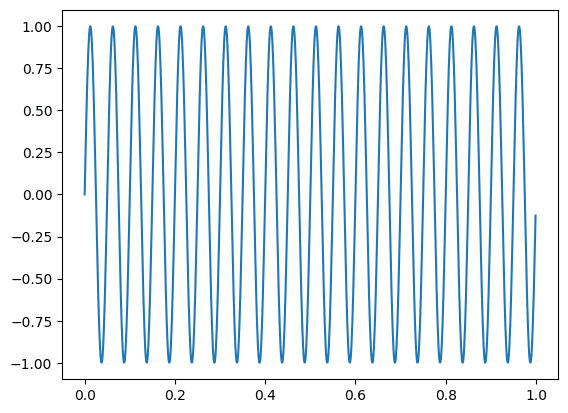
それでは始めていきましょう。
scipy.fftによる高速フーリエ変換
scipy.fftを用いて高速フーリエ変換をするにはまずはscipy.fftのfftをインポートします。
from scipy.fft import fftそして高速フーリエ変換したいデータをfft関数に渡す、つまり「fft(データ)」とするだけです。
少し手間がかかるのが横軸となる周波数を取得する方法と強度を算出する方法です。
周波数を取得するにはnumpyの「np.fft.fft.freq(サンプル数, サンプリングレート)」を用います。
また強度を取得するには「abs(fft後のデータ/サンプル数/2)」とします。
周波数と強度の算出はNumPyを使って高速フーリエ変換する際と同じですので、こちらの記事も参考にしてください。

ということでこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
time = np.arange(0, 1, 0.001)
y = np.sin(20*2*np.pi*time)
y_fft = fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
fig = plt.figure()
plt.clf()
plt.plot(freq, Amp)
plt.xlim(0, 50)
plt.show()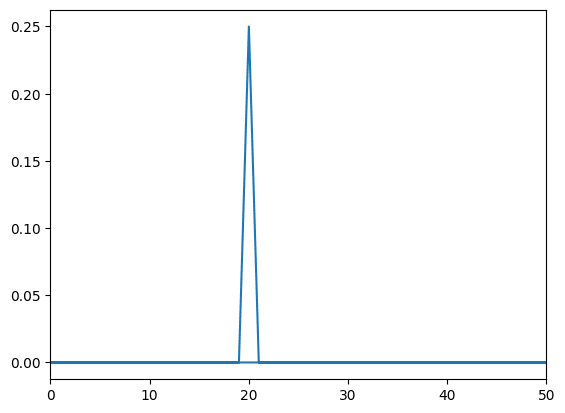
scipy.fftとnumpy.fft.fftの処理速度の比較
scipy.fftとnumpy.fft.fftの処理速度の比較をしてみました。
比較するのは先ほどのプログラムですが、純粋に高速フーリエ変換の処理時間を比較したいため、matplotlibによるグラフ化の部分は削除しました。
そしてマジックコマンド「%%timeit」を使って処理時間の比較を行いました。
%%timeit
import numpy as np
from scipy.fft import fft
time = np.arange(0, 1, 0.001)
y = np.sin(20*2*np.pi*time)
y_fft = fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
実行結果
65.7 µs ± 2.59 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)%%timeit
import numpy as np
time = np.arange(0, 1, 0.001)
y = np.sin(20*2*np.pi*time)
y_fft = np.fft.fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
実行結果
62.1 µs ± 2.37 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)scipy.fftは65.7μ秒、numpy.fft.fftは62.1μ秒ということで大きな違いは出ませんでした。
サンプル数の違いによる処理速度の比較
高速フーリエ変換ではデータ数が2のべき乗となる場合、データ数が2のべき乗でない場合と比べて特に高速に処理できるそうです。
ということで同じ範囲のデータを1024個、1023個、1025個に分割してscipy.fftで処理してみました。
%%timeit
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
time = np.linspace(0, 1, 1024)
y = np.sin(20*2*np.pi*time)
y_fft = fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
実行結果
117 µs ± 14.8 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)%%timeit
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
time = np.linspace(0, 1, 1023)
y = np.sin(20*2*np.pi*time)
y_fft = fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
実行結果
129 µs ± 7.41 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)%%timeit
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
time = np.linspace(0, 1, 1025)
y = np.sin(20*2*np.pi*time)
y_fft = fft(y)
interval = time[1] - time[0]
freq = np.fft.fftfreq(len(y), interval)
Amp = abs(y_fft/len(y)/2)
実行結果
118 µs ± 4.3 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)今回、データ数が1024の場合の処理時間は117μ秒、1023の場合の処理時間は129μ秒、1025の場合の処理時間は118μ秒と大きな違いは見られませんでした。
ただデータ数が大きくないですし、データ自体も複雑でないことからあまり差が出なかった可能性も考えられます。
データ数が2のべき乗にならない場合は前後を0で埋めてデータ数を2のべき乗にするというテクニックがあるらしいので、またそういったデータに出会った場合、試してみたいと思います。
次回はNumPyで配列を連結する方法(np.hstack、np.vstack、np.dstack、np.concatenate、np.block)を紹介します。
ではでは今回はこんな感じで。

コメント