補完(interpolation)
前回、Pythonでリストの要素を飛び飛び(X個おき)に取得する方法を紹介しました。
今回はデータを補完(interpolation)する方法を紹介します。
補完とはデータの並び方を推測し、その間のデータを追加することをいいます。
データの値の数が少なかったり、欠損がある場合、前後のデータの並び方を解析することにより、その欠損した値を推測し、追加することでデータの精度を上げるのに役立ちます。
例えばこんなグラフがあったとします。
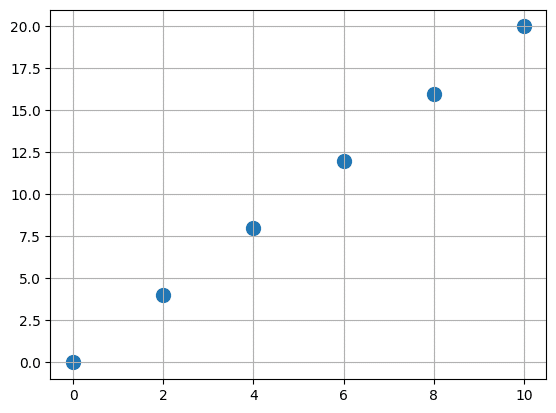
グラフ上には6つの点が表示されており、Xが0、Yが0の点から始まり、Xが10、Yが20となっています。
6つの点の変化からこのグラフは「y = 2x」だと推測し、その間の点をさらに細かく取ったのがこちらです。

このようにデータとしては取得できていない値を、何らかの数学的な推測により埋めるという方法を補完と言います。
そして補完には色々な式が存在します。
PythonではSciPyライブラリの中にinterpolationというモジュールがあり、簡単にデータの補完を行うことができます。
それでは始めていきましょう。
使用するデータの作成
まずは今回使用するデータを作成します。
今回はsin波を作成し、データをわざと欠損させて、それを補完してみましょう。
ということで欠損させる前のsin波のデータをこんな感じで準備しました。
import matplotlib.pyplot as plt
import numpy as np
n = 3
x = range(0, 360)
y = [np.sin(i*np.pi/180*n) for i in x]
fig=plt.figure()
plt.scatter(x,y)
plt.grid()
plt.show()
作成したXの値とYの値を10個おきに取得することで、わざと欠損したデータにしました。
import matplotlib.pyplot as plt
import numpy as np
n = 3
x = range(0, 360)
y = [np.sin(i*np.pi/180*n) for i in x]
x_less = x[::10]
y_less = y[::10]
fig=plt.figure()
plt.scatter(x_less,y_less)
plt.grid()
plt.show()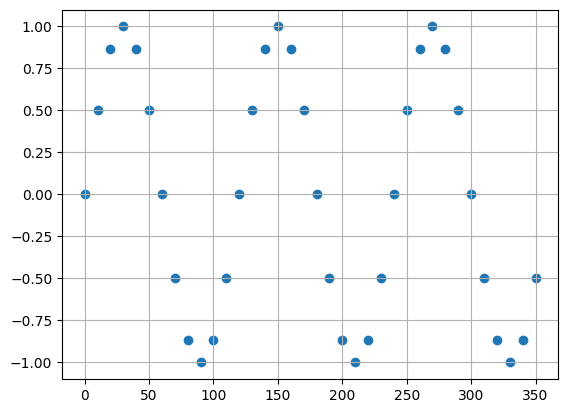
一次元補完:interpolate.interp1d
とりあえず試してみると言うことなら、一次元補完を試してみるのがいいでしょう。
一次元補完とは、例えば2つの点の間を直線として推測し、補完を行う線形補完が含まれます。
SciPyではinterpolate.interp1dという関数のデフォルトではこの線形補完が使われます。
基本的な使い方としては「変数 = interpolate.interp1d(x, y)」で、補完用の式を作成し、それに対して補完後のXの系列を渡します。
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
n = 3
x = range(0, 360)
y = [np.sin(i*np.pi/180*n) for i in x]
x_less = x[::10]
y_less = y[::10]
fig=plt.figure()
plt.scatter(x_less,y_less)
interp = interpolate.interp1d(x_less, y_less)
x_new = np.linspace(0, x_less[-1], num=720)
y_new = interp(x_new)
plt.scatter(x_new, y_new, s=5)
plt.grid()
plt.show()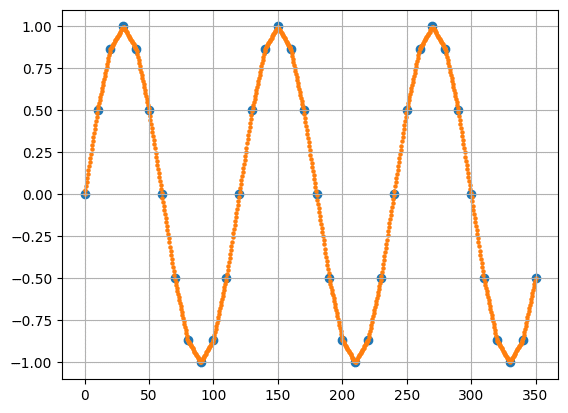
この例では「interp = interpolate.interp1d(x_less, y_less)」で補完用の式を作成、また「x_new = np.linspace(0, x_less[-1], num=720)」で新しいXの系列を作成し、「y_new = interp(x_new)」で新しいYの系列を作成しています。
ちなみに「np.linspace(最初の値, 最後の値, 分割数)」で最初の値から最後の値までを分割数で分割したリストを取得することができます。
例えば「np.linspace(0, 10, 101)」であれば、0から10までを101分割した「0, 0.1, 0.2, 0.3, …」というリストが得られます。
interpolate.interp1dには他の一次元補完の関数もあり、「kind」というオプションを追加することで選択できます。
選択肢としてはデフォルトの「linear」の他、「nearest」、「nearest-up」、「zero」、「slinear」、「quadratic」、「cubic」、「previous」、「next」があります。
詳しくは公式サイトをご確認ください。
他の補完方法
補完の方法には一次元補完のほかに多次元補完とか色々とあるようです。
ここで全てを紹介するのは大変なので、どんなものがあるのかは公式サイトをご覧ください。
基本的に使い方はinterpolation.interp1d(x, y)と同じです。
補完の方法によっては全くの的外れなこともありますし、ものすごく正解近くまで補完してくれるものもありますので、実際に使う際にはどの関数を選択するのかは注意する必要があるでしょう。
次回はPythonでランダムな波形を作成する方法を紹介します。

ではでは今回はこんな感じで。

コメント