MENU
大人のためのSTEM遊び場〜Python、3Dプリンタ、ガジェット〜
  1. ホーム
  2. Programming
  3. 【SciPy】短時間フーリエ変換（STFT：Short-time Fourier Transform）による時間周波数解析[Python]

【SciPy】短時間フーリエ変換（STFT：Short-time Fourier Transform）による時間周波数解析[Python]

Programming
Python scipy プログラミング 数値計算
  • URLをコピーしました！
目次

短時間フーリエ変換

前回、Pythonで時間変化のあるランダムな波形を作成する方法を紹介しました。

あわせて読みたい
【Python】時間変化のあるランダムな波形を作成する方法 【ランダムな波形】 前回、正規分布（ガウス分布）を使い、脳波のα波、β波、θ波のような波形を作成する方法を紹介しました。 今回はさらに時間で異なるランダムな波形に…

今回はその時間変化のあるランダムな波形を使って、経時的な変化を視覚的に確認できる方法を紹介します。

その方法は短時間フーリエ解析による時間周波数解析です。

ここで前回のプログラムと出力をおさらいしてみましょう。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]

samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])

preview_time_list = [[5, 15], [30, 40], [65, 75]]

for preview_time in preview_time_list:
    fig = plt.figure()
    plt.clf()
    plt.plot(df_integrate["Time"], df_integrate["SUM"])
    plt.grid()
    plt.xlabel("Time(sec)")
    plt.ylabel("Amplitude")
    plt.xlim(preview_time[0], preview_time[1])
    plt.show()

    start_row = preview_time[0]*samplingrate
    end_row = preview_time[1]*samplingrate
    fft_data = np.fft.fft(df_integrate["SUM"][start_row:end_row])
    freq = np.fft.fftfreq(len(df_integrate["SUM"][start_row:end_row]), 1/samplingrate)
    Amp = abs(fft_data/(len(df_integrate["SUM"][start_row:end_row])/2))

    fig = plt.figure()
    plt.clf()
    plt.plot(freq[1:int(len(df_integrate["SUM"][start_row:end_row])/2)], Amp[1:int(len(df_integrate["SUM"][start_row:end_row])/2)])
    plt.xlim(0,50)
    plt.xlabel("Frequency(Hz)")
    plt.ylabel("Amplitude")
    plt.show()
    
fig = plt.figure()
plt.clf()
plt.plot(df_integrate["Time"], df_integrate["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.show()
    
fft_data = np.fft.fft(df_integrate["SUM"])
freq = np.fft.fftfreq(len(df_integrate["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df_integrate["SUM"])/2))

fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df_integrate["SUM"])/2)], Amp[1:int(len(df_integrate["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()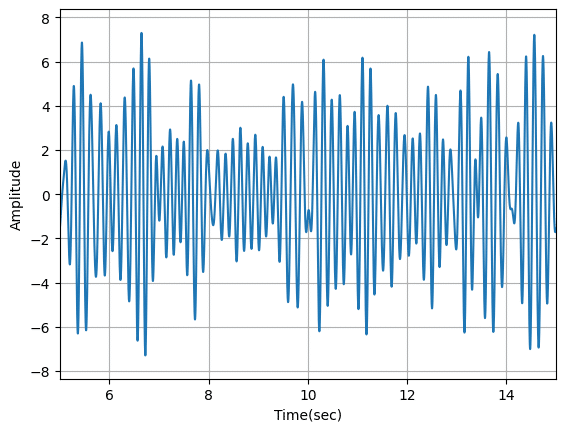

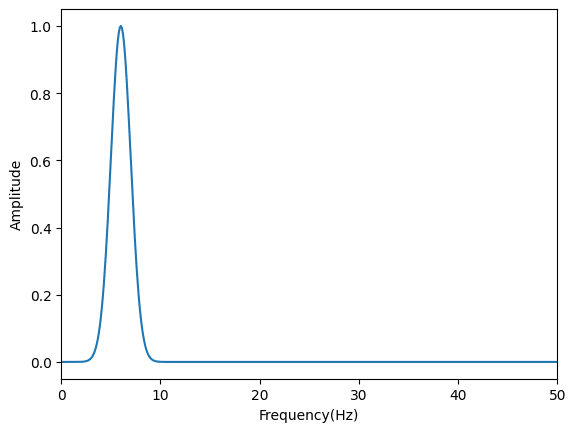
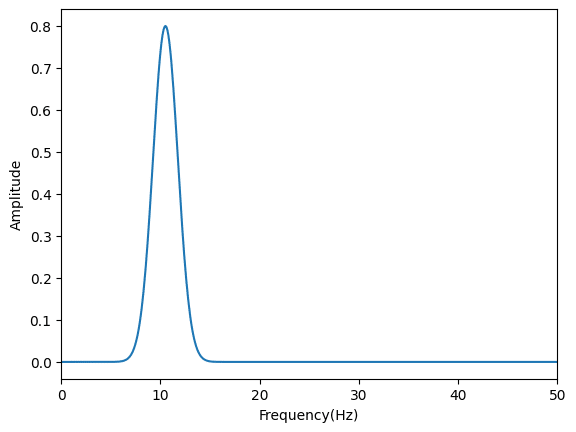
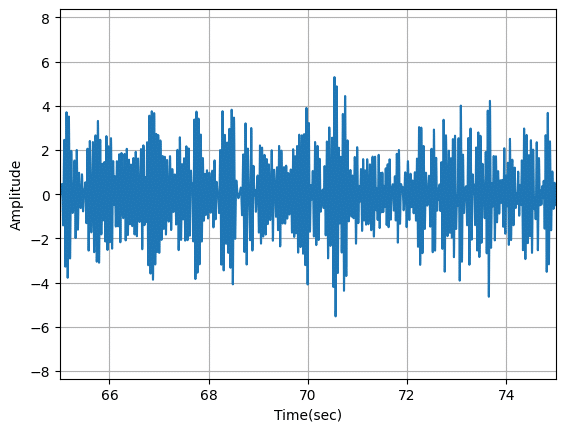
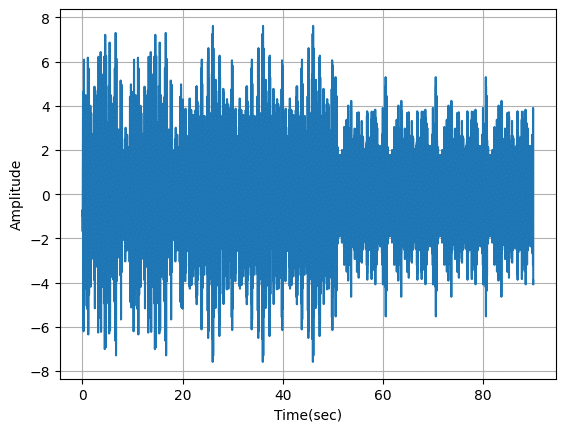
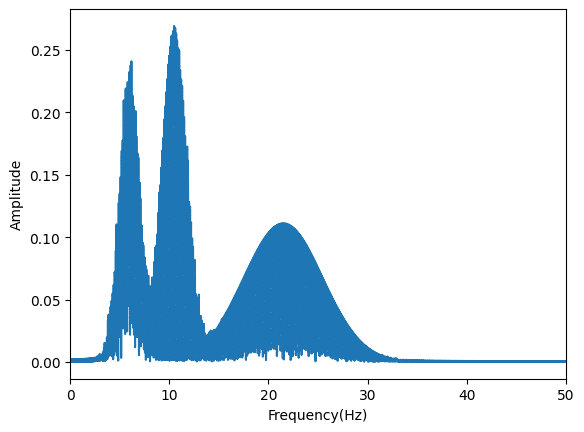
今回は0から20秒がθ波、20秒から50秒がα波、50秒から90秒がβ波になっています。

そのため5から15秒を表示した1枚目、FFT解析した2枚目はθ波を、30から40秒を表示した3枚目、FFT解析した4枚目はα波を、65から75秒を表示した5枚目、FFT解析した6枚目はβ波を示しているのが分かります。

そして全体を表示した7枚目、FFT解析した8枚目では全てが混ざっているため、どの時間にどの周波数が強いのかは分かりません。

今回行う短時間フーリエ変換による時間周波数解析では、データを短時間に分割、フーリエ変換し、縦軸に周波数、横軸に時間、色でその強度を示すことから、時間や強度の変化が視覚的に理解しやすくなる方法です。

例えば先ほどのプログラムで作成した波を短時間フーリエ変換してみるとこんな感じになります。

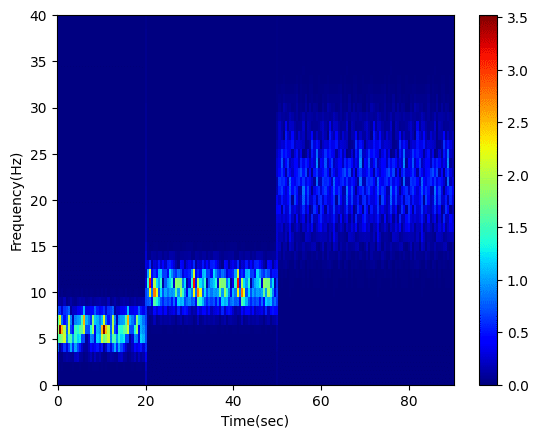
まさに一目瞭然で時間経過に対する周波数、ならびに強度の変化が分かるというのを理解してもらえたかと思います。

それでは始めていきましょう。

SciPyによるSTFT

今回、SciPyを用いて短時間フーリエ変換（STFT）を行います。

インポートするのはSciPyの中の「signal」モジュールです。

from scipy import singal

そしてデータを短時間フーリエ解析するには「signal.stft」を用います。

freq, ts, Zxx = signal.stft(波のデータ, fs=サンプリングレート)

freqが周波数のデータ、tsは時間のデータ、Zxxが特定の時間、特定の周波数における強度のデータになります。

このままでは数値データなので、グラフに変換しますが、その際にはMatplotlibの「pcolormesh」を用います。

（というわけでmatplotlib.pyplotのインポートをお忘れなく）

plt.pcolormesh(stftのts, stftのfreq, np.abs(stftのZxx), cmap="jet")

短時間フーリエ解析を行うとFFT（高速フーリエ変換）の時と同様に強度の値は複素数で得られますが、やはり実数部分のみが必要であるため、「np.abs」で絶対値を取得します。

これで短時間フーリエ解析とグラフ化ができます。

ということで全体的にはこんな感じ。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
from scipy import signal

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]

samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])
    
freq, ts, Zxx = signal.stft(df_integrate["SUM"], fs=samplingrate)
plt.pcolormesh(ts, freq, np.abs(Zxx), cmap="jet")
plt.ylim(0, 40)
plt.colorbar()
plt.xlabel("Time(sec)")
plt.ylabel("Frequency(Hz)")
plt.show()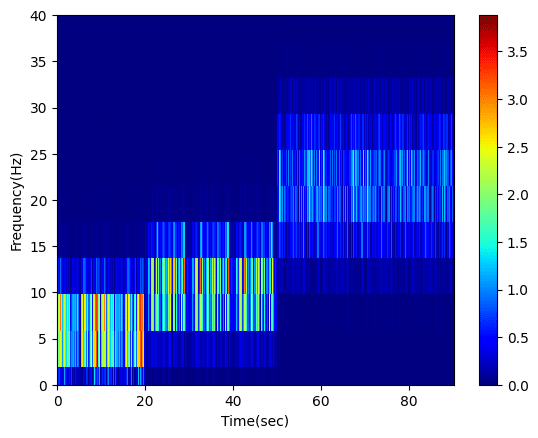

確かにグラフが出力されたのですが、時間に対する分解能はいいのですが、波長に対する分解能が悪いです。

短時間フーリエ解析では窓関数を使ってデータを切り分けていきますが、その際にどれくらいの長さの窓を切り出すかによって時間分解能、周波数分解能が変わります。

あわせて読みたい
窓関数 – Wikipedia

そして短時間フーリエ解析では時間分解能と周波数分解能はトレードオフの関係にあり、時間分解能が高ければ周波数分解能は低く、逆に時間分解能が低ければ周波数分解能が高くなります。

その切り出すサイズを設定する項目が「nperseg」です。

nperseg

npersegのデフォルト値は512です。

この値を大きくすると時間分解能が低く、周波数分解能が高くなります。

先ほどの例では時間分解能が高く、周波数分解能が低かったので、倍の値「1024」にしてみましょう。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
from scipy import signal

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]

samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])
    
freq, ts, Zxx = signal.stft(df_integrate["SUM"], fs=samplingrate, nperseg=1024)
plt.pcolormesh(ts, freq, np.abs(Zxx), cmap="jet")
plt.ylim(0, 40)
plt.colorbar()
plt.xlabel("Time(sec)")
plt.ylabel("Frequency(Hz)")
plt.show()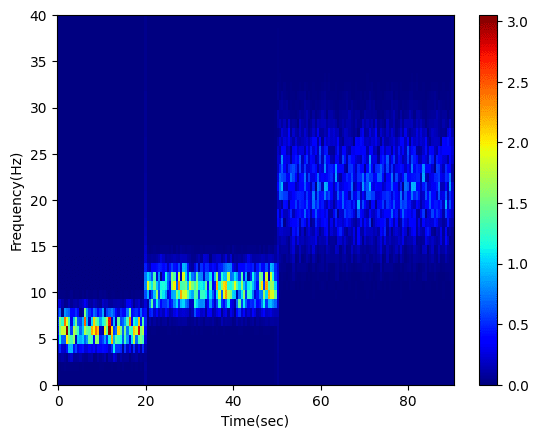

最初に紹介したような時間分解能も周波数分解能もちょうどいいグラフになりました。

それでは極端な値として「npersegが100」の場合と「npersegが10000」の場合を試してみましょう。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
from scipy import signal

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]

samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])
    
freq, ts, Zxx = signal.stft(df_integrate["SUM"], fs=samplingrate, nperseg=100)
plt.pcolormesh(ts, freq, np.abs(Zxx), cmap="jet")
plt.ylim(0, 40)
plt.colorbar()
plt.xlabel("Time(sec)")
plt.ylabel("Frequency(Hz)")
plt.show()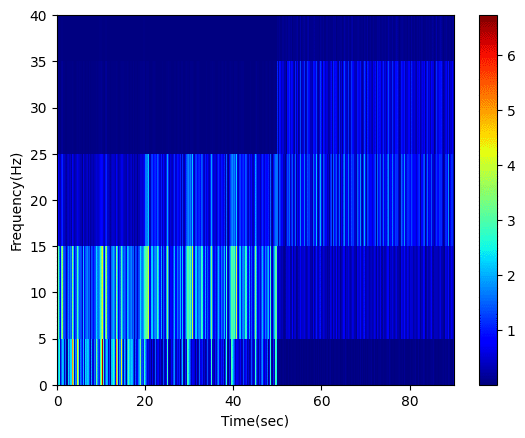
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
from scipy import signal

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]

samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])
    
freq, ts, Zxx = signal.stft(df_integrate["SUM"], fs=samplingrate, nperseg=10000)
plt.pcolormesh(ts, freq, np.abs(Zxx), cmap="jet")
plt.ylim(0, 40)
plt.colorbar()
plt.xlabel("Time(sec)")
plt.ylabel("Frequency(Hz)")
plt.show()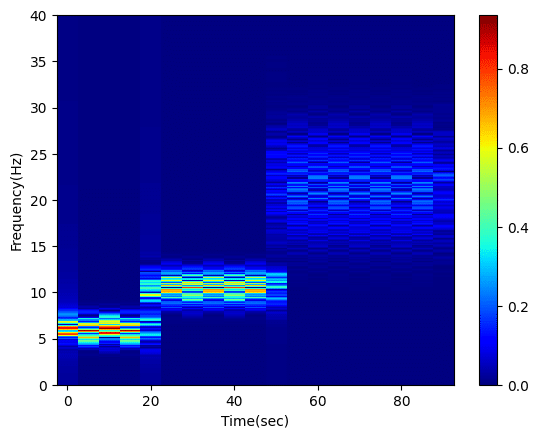

やはりnpersegが小さいと時間分解能が高く、周波数分解能が低くなり、またnpersegが大きいと時間分解能が低く、周波数分解能が高くなることが分かります。

ということで波に関して色々試してきましたが、なかなか面白いのでまた色々といじってみたいと思います。

次回はPythonの基礎に戻ってプログラムを終了させるsys.exitを紹介します。

あわせて読みたい
【Python基礎】プログラムを終了させる方法：sys.exit() 【プログラムの終了】 前回、SciPyを使った短時間フーリエ変換による時間周波数解析の方法を紹介しました。 今回はもっと基礎的なことでPythonのプログラムを終了させる…

ではでは今回はこんな感じで。

Programming
Python scipy プログラミング 数値計算
よかったらシェアしてね！
  • URLをコピーしました！

コメント

コメントする

目次