NetworkX
前回、Pythonでネットワーク作成ライブラリNetworkXでNodeの形状を変える方法を試してみました。
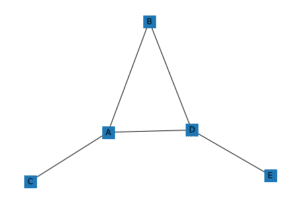
これまでにNodeとEdgeの形や色を変える方法は色々試してきたわけですが、もう一つ重要なのがネットワーク自体の形を変えることです。
NetworkXにはもちろんそのような機能が備わっているので、今回試していきたいと思います。
というわけで基本となるプログラムはこちら。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
nx.draw(G, with_labels = True)
実行結果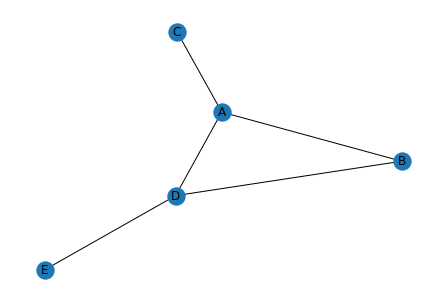
それでは始めていきましょう。
ポジションの基本
まずNodeの位置を指定することで、ネットワークの形状を変える方法です。
その場合は「nx.draw」に「pos」のオプションを追加します。
この「pos」のオプションに入れる値は、辞書形式で「{ノード名:[X値、Y値], …}」と指定していきます。
ということでこんな感じです。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = {'A':[0,0], 'B':[1, 1], 'C':[1, -1], 'D':[-1, 1], 'E':[-1, -1]}
nx.draw(G, pos, with_labels = True)
実行結果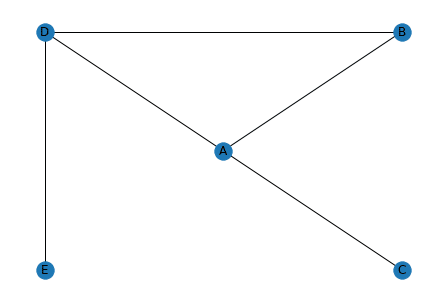
このposを指定してネットワーク図を描いた場合、毎回同じネットワーク図が出力されます。
spring_layout
ここからはposを自分で指定せず、ライブラリの機能によって計算、指定するコマンドを見ていきましょう。
まずは「nx.spring_layout」です。
こちらはNode間に反発力を与え、またEdgeに与えられた「weight」の値によって引力を与えることでNode間の距離を調節するようになっています。
Node間の反発に関しては「nx.spring_layout(G, k=反発力の値)」の「k」の値を変えることで調節します。
「k」が大きくなるとNode間が強く反発するようになるので、全体的に円形になります。
またEdgeの「weight」に関しては、「.add_edge」のオプションで「weight」を追加します。
ということでこんな感じ。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B', weight=1)
G.add_edge('A', 'C', weight=2)
G.add_edge('A', 'D', weight=3)
G.add_edge('B', 'D', weight=4)
G.add_edge('D', 'E', weight=5)
pos = nx.spring_layout(G, k=2)
nx.draw(G, pos, with_labels = True)
実行結果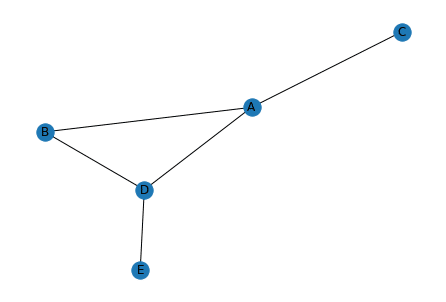
この「spring_layout」の場合、調節しているのはノード間の距離だけですので、出力する毎に形状は変化します。
bipartite_layout
「bipartite_layout」はNodeが左右に分かれて配置されるレイアウトです。
nx.bipartite_layout(G, [左側に配置するNodeのリスト])として、左側に配置するNodeを指定する引数が必要です。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.bipartite_layout(G, ['A', 'B', 'C'])
nx.draw(G, pos, with_labels = True)
実行結果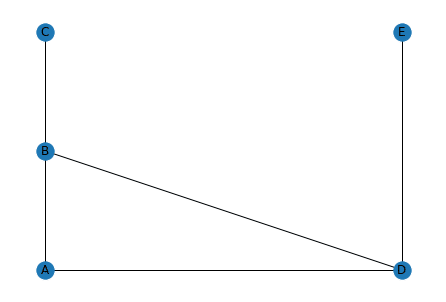
今回の基本のプログラムを使って出力するとこのようになってしまって、あまり「bipartite_layout」を使った意味を成さないので、Edgeの組み合わせを変えてみます。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'D')
G.add_edge('A', 'E')
G.add_edge('B', 'D')
G.add_edge('B', 'E')
G.add_edge('C', 'D')
pos = nx.bipartite_layout(G, ['A', 'B', 'C'])
nx.draw(G, pos, with_labels = True)
実行結果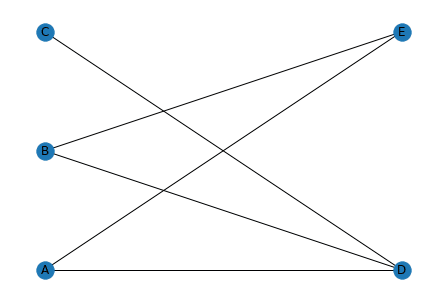
こんな感じでマッチングのようにして使うのが良さそうです。
「bipartite_layout」は毎回同じ結果を出力してくれます。
circular_layout
「circular_layout」はNodeを円状に並べるレイアウトです。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.circular_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果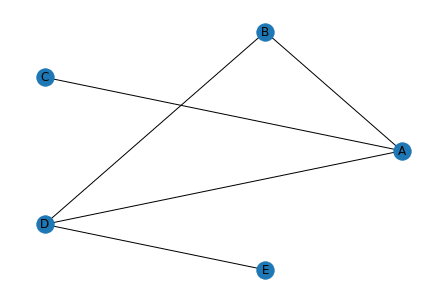
特にオプションや引数も必要ないので楽ちんです。
こちらも毎回同じ結果を出力してくれるようです。
kamada_kawai_layout
「kamada_kawai_layout」はよく分からないですが、NetworkXの公式サイトでは「Kamada-Kawai path-length cost-function」と書かれているので、Edgeの長さに制限を与えるレイアウトのようです。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.kamada_kawai_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果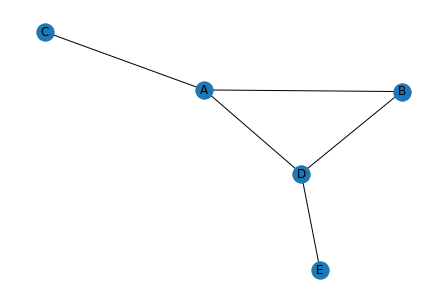
「kamada_kawai_layout」では毎回同じ結果が出力されるようです。
planar_layout
「planar_layout」はEdgeが交差しないように配置するレイアウトです。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.planar_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果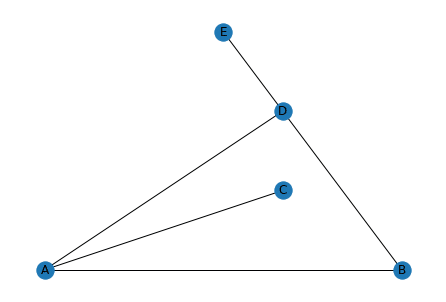
random_layout
「random_layout」はその名の通りNodeをランダムに配置します。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.random_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果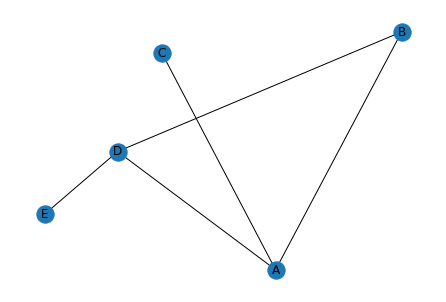
shell_layout
「shell_layout」は「circular_layout」と似ていて何がどう違うのかちょっと分かりません。
「circular_layout」は丸で「shell_layout」は楕円という感じなのでしょうか。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.shell_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果もっとNodeの数を増やせば違いが分かるかもしれませんので、ご興味ある方はやってみてください。
spectral_layout
「spectral_layout」はよく分かりません。
公式サイトでは「Position nodes using the eigenvectors of the graph Laplacian.」と書かれていて固定ベクトルなるものを使って計算をしているようです。
ここら辺はちゃんと数学を学ばないと理解できなさそうですね。
とりあえず下向きの谷のような形になるようです。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.spectral_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果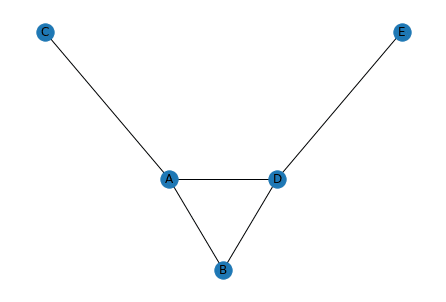
spiral_layout
「spiral_layout」もよく分かりませんが、らせん状になるレイアウトではないかなと思います。
import networkx as nx
G = nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_node('D')
G.add_node('E')
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.spiral_layout(G)
nx.draw(G, pos, with_labels = True)
実行結果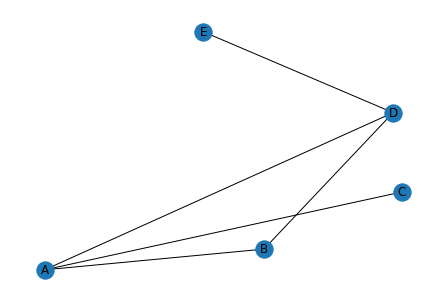
multipartite_layout
「multipartite_layout」は「bipartite_layout」の複数版です。
「add_node」の際に「subset」のオプションを与え、どのカテゴリにいるNodeか指定します。
import networkx as nx
G = nx.Graph()
G.add_node('A', subset=1)
G.add_node('B', subset=1)
G.add_node('C', subset=2)
G.add_node('D', subset=2)
G.add_node('E', subset=3)
G.add_edge('A', 'B')
G.add_edge('A', 'C')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
pos = nx.multipartite_layout(G)
nx.draw(G, pos, with_labels = True)
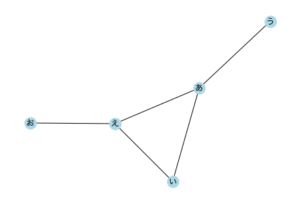
実行結果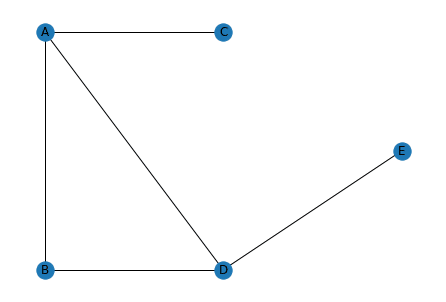
これでポジションのオプションを使ったネットワークの形状は全てです。
ちなみに「rescale_layout」や「rescale_layout_dict」というコマンドもあり、ネットワーク図の大きさを変えることもできるようですが、あまり使うこともないと思うので、今回は割愛します。
次回はNetworkXのフォントを指定し、日本語を表示させる方法を試していきましょう。
ではでは今回はこんな感じで。

コメント