【Python】時間変化のあるランダムな波形を作成する方法

2023年9月27日2023年11月18日

URLをコピーしました！

ランダムな波形

前回、正規分布（ガウス分布）を使い、脳波のα波、β波、θ波のような波形を作成する方法を紹介しました。

あわせて読みたい

【Python】正規分布（ガウス分布）を使い、脳波のα波、β波、θ波のような波形を作成してみた正規分布前回、NumpyのFFT（高速フーリエ変換）を使って周波数解析をする方法を紹介しました。今回はPythonで正規分布（ガウス分布）のデータを作成する方法を紹介し…

今回はさらに時間で異なるランダムな波形になるようにしてみたいと思います。

まずは前回のおさらいです。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz

data_list = [np.arange(0, time, 1/samplingrate)]

for hz, w in zip(hz_range, hz_weight):
    if w == 0:
        weight = random.random()
    else:
        weight = w
        
    fai = random.random() * 2*np.pi
    data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
    
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")

df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")

df["SUM"] = df.iloc[:, 1:].sum(axis=1)

fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()

fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))

fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()

長く見えますが、「df[“SUM”] = df.iloc[:, 1:].sum(axis=1)」より後はグラフ表示のためなので、気にしなくて大丈夫です。

ランダムな波形の時間は「df[“Time”]」に、シグナル強度は「df[“SUM”]」に格納されています。

それでは始めていきましょう。

時間で変化させるプログラム

まずはプログラム全体をお見せします。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random

def gauss(x_list, a=1, m=0, s=1):
    y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
    return y_list

time_list = [20, 30, 40]
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]
    
    for hz, w in zip(hz_range, hz_weight):
        if w == 0:
            weight = random.random()
        else:
            weight = w

        fai = random.random() * 2*np.pi
        data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))

    columnnames = [hz for hz in hz_range]
    columnnames.insert(0, "Time")

    df = pd.DataFrame(data_list).transpose()
    df = df.set_axis(columnnames, axis="columns")

    df["SUM"] = df.iloc[:, 1:].sum(axis=1)
    df_integrate = pd.concat([df_integrate, df])

preview_time_list = [[5, 15], [30, 40], [65, 75]]

for preview_time in preview_time_list:
    fig = plt.figure()
    plt.clf()
    plt.plot(df_integrate["Time"], df_integrate["SUM"])
    plt.grid()
    plt.xlabel("Time(sec)")
    plt.ylabel("Amplitude")
    plt.xlim(preview_time[0], preview_time[1])
    plt.show()

    start_row = preview_time[0]*samplingrate
    end_row = preview_time[1]*samplingrate
    fft_data = np.fft.fft(df_integrate["SUM"][start_row:end_row])
    freq = np.fft.fftfreq(len(df_integrate["SUM"][start_row:end_row]), 1/samplingrate)
    Amp = abs(fft_data/(len(df_integrate["SUM"][start_row:end_row])/2))

    fig = plt.figure()
    plt.clf()
    plt.plot(freq[1:int(len(df_integrate["SUM"][start_row:end_row])/2)], Amp[1:int(len(df_integrate["SUM"][start_row:end_row])/2)])
    plt.xlim(0,50)
    plt.xlabel("Frequency(Hz)")
    plt.ylabel("Amplitude")
    plt.show()
    
fig = plt.figure()
plt.clf()
plt.plot(df_integrate["Time"], df_integrate["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.show()
    
fft_data = np.fft.fft(df_integrate["SUM"])
freq = np.fft.fftfreq(len(df_integrate["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df_integrate["SUM"])/2))

fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df_integrate["SUM"])/2)], Amp[1:int(len(df_integrate["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()

「preview_time_list = [[5, 15], [30, 40], [65, 75]]」以降はグラフ表示のためのプログラムなので、詳細は省きます。

変更点としては、まずは時間をリストとして複数格納したこと、また周波数に対するシグナル強度を複数用意し、リストに格納したことです。

time_list = [20, 30, 40]
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight1 = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
hz_weight2 = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight3 = gauss(hz_range, a=1/4, m=21.5, s=4) #14 - 30 Hz

hz_list = [hz_weight1, hz_weight2, hz_weight3]

そして周波数強度のリストから一つずつ要素を取り出しデータを作成していきますが、その際、時間のリストを使って、それぞれの時間範囲をリストに格納しています。

df_integrate = pd.DataFrame()
for i, hz_weight in enumerate(hz_list):
    data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/samplingrate)]

そしてそれぞれの時間範囲で作成したデータフレームを最後に結合します。

df_integrate = pd.concat([df_integrate, df])

これを実行するとこんな感じのグラフが得られます。

θ波の部分（5秒から15秒を拡大）。

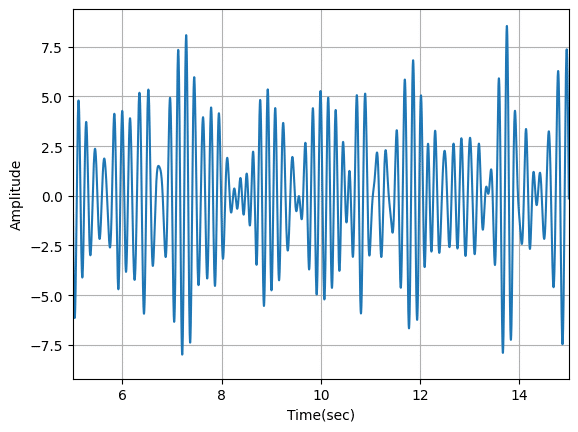
α波の部分（30秒から40秒を拡大）。

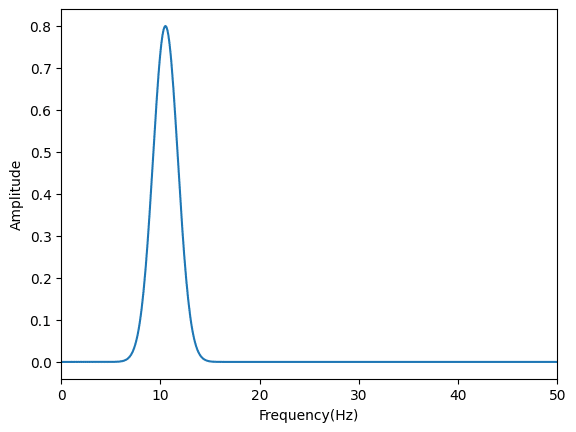
β波の部分（65秒から75秒を拡大）。

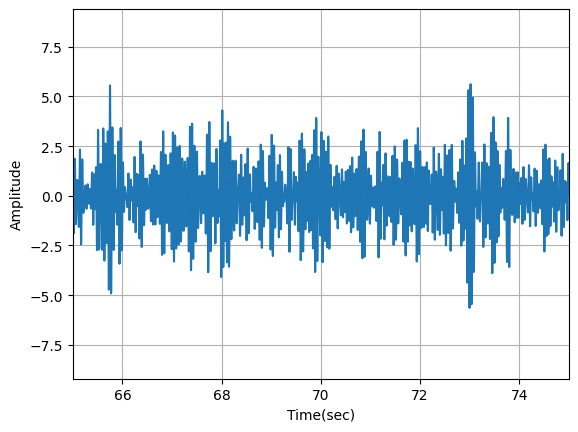
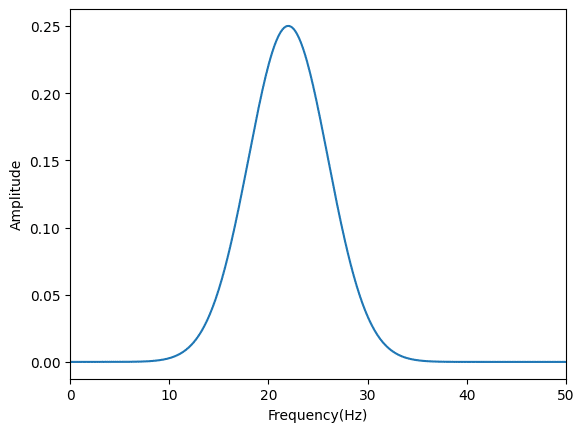
全体。

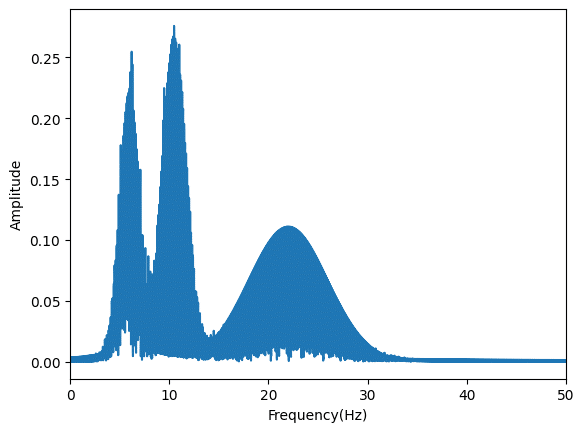
1秒とかミリ秒単位の変化ではありませんが、ある程度の時間帯で波形を変化させることができました。

クラス化

これでランダムな波形を作るプログラムができたので、クラスにしておきました。

import numpy as np
import pandas as pd
import random

class WaveGenerator:
    def __init__(self, samplingrate):
        self.samplingrate = samplingrate
        
    def randomwave(self, time_list, hz_range_list, hz_weight_list, hz_fai_list):
        df_integrate = pd.DataFrame()
        for i, (hz_range, hz_weight, hz_fai) in enumerate(zip(hz_range_list, hz_weight_list, hz_fai_list)):
            data_list = [np.arange(sum(time_list[:i]), sum(time_list[:i+1]), 1/self.samplingrate)]
            
            for hz, w, fai in zip(hz_range, hz_weight, hz_fai):
                data_list.append(w * np.sin(2*np.pi*hz*data_list[0] + fai))
                
            columnnames = [hz for hz in hz_range]
            columnnames.insert(0, "Time")

            df = pd.DataFrame(data_list).transpose()
            df = df.set_axis(columnnames, axis="columns")
            df["SUM"] = df.iloc[:, 1:].sum(axis=1)
            df_integrate = pd.concat([df_integrate, df])
        return df_integrate
    
    def gauss(self, x_list, a=1, m=0, s=1):
        y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
        return y_list
    
    def theta(self, x_list):
        return WaveGenerator.gauss(self, x_list, a=1, m=6, s=1)
    
    def alpha(self, x_list):
        return WaveGenerator.gauss(self, x_list, a=1/1.25, m=10.5, s=1.25)
        
    def beta(self, x_list):
        return WaveGenerator.gauss(self, x_list, a=1/14, m=21.5, s=4)

インスタンス化する際にサンプリングレートを渡しておき、「randomwave関数」に時間のリスト、波長域のリスト、波長に対するシグナル強度のリスト、位相のリストを渡すと波形を生成し、データフレームとして返してくれます。

またガウス関数だけでなく、「theta関数」、「alpha関数」、「beta関数」があり、波長域のリストを渡すことで、それぞれθ波、α波、β波を作成してくれます。

次回はScipyでSTFT（短時間フーリエ変換）をして経時的な波長の変化をグラフ化してみましょう。