正規分布
前回、NumpyのFFT(高速フーリエ変換)を使って周波数解析をする方法を紹介しました。
今回はPythonで正規分布(ガウス分布)のデータを作成する方法を紹介します。
そしてその正規分布を使って、脳波のα波、β波、ガンマ派のような波形を作成してみましょう。
まず正規分布(ガウス分布)に関してですが、これは確率論や統計論で用いられる分布の一つで、値が平均値が一番高く、左右対称に減少していく分布のことを言います。
正規分布に関しての詳しい解説はWikipediaを始め、他のサイトを参考にしてください。
ガウス関数
正規分布を得るためにはガウス関数なる式を使用します。
\(f(x) = a \times exp \{ – \frac{(x – \mu)^2}{2\sigma^2}\}\)
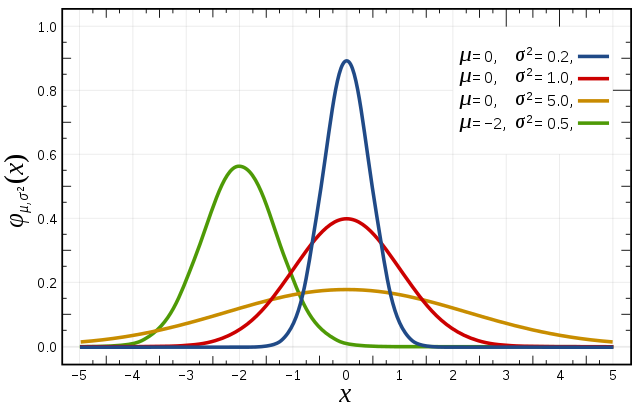
aはピークの高さを、μは中心の位置を、σは広がりを決める値です。
これを関数化してみるとこんな感じです。
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_listこれで「x_list」にX軸方向の値のリストを渡すと正規分布を返してくれます。
その際にa、m(=μ)、s(=σ)の値をオプションとして追加すると、それらの値にあった正規分布を返してくれます。
とりあえず-10から10までの範囲(0.1刻み)でa=1、μ=0、σ=1(つまりデフォルト)の正規分布を出力してみます。
import numpy as np
import matplotlib.pyplot as plt
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(-10,10, 0.1)
y1 = gauss(x)
fig = plt.figure()
plt.plot(x, y1)
plt.show()
これを基準にa、μ、σを変えてみましょう。
まずはaを2にしてみます。
import numpy as np
import matplotlib.pyplot as plt
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(-10,10, 0.1)
y1 = gauss(x)
y2 = gauss(x, a=2)
fig = plt.figure()
plt.plot(x, y1)
plt.plot(x, y2)
plt.show()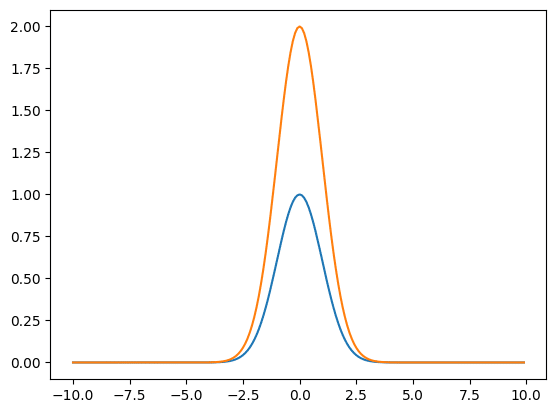
ピークの高さが2倍になりました。
次にμを1に変えてみます。
import numpy as np
import matplotlib.pyplot as plt
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(-10,10, 0.1)
y1 = gauss(x)
y2 = gauss(x, m=1)
fig = plt.figure()
plt.plot(x, y1)
plt.plot(x, y2)
plt.show()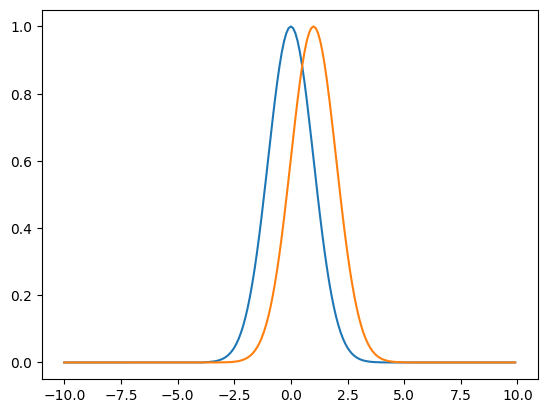
ピークの位置が右に1ずれました。
最後にσを2にしてみます。
import numpy as np
import matplotlib.pyplot as plt
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(-10,10, 0.1)
y1 = gauss(x)
y2 = gauss(x, s=2)
fig = plt.figure()
plt.plot(x, y1)
plt.plot(x, y2)
plt.show()
ピークの幅が広がりました。
脳波のような分布を作成
次にこの正規分布を使って、脳波のような分布を作成していきます。
脳波にはδ波、θ波、α波、β波、γ波などがあり、それぞれ意味が異なってきます。
| 名称 | 周波数 | 状態 |
| δ(デルタ)波 | 4 Hz 以下 | 熟睡 |
| θ(シータ)波 | 4 〜 8 Hz | うたた寝 |
| α(アルファ)波 | 8 〜 13 Hz | リラックス |
| β(ベータ)波 | 13 〜 30 Hz | 覚醒状態 |
| γ(ガンマ)波 | 30 Hz 以上 | 興奮状態 |
今回はθ波、α波、β波のような分布を作成してみます。
ピーク周波数を各脳波帯域の中心とし、波長域が広いものほどピークの強度を低く、広がりを広くしてみました。
今回の設定値はあくまでも一例なので、自分で色々いじってもらえるといいかと思います。
import numpy as np
import matplotlib.pyplot as plt
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(0,40, 0.1)
theta = gauss(x, a=1/1, m=6, s=1) #4 - 8 Hz
alpha = gauss(x, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
beta = gauss(x, a=1/4, m=21.5, s=4) #13 - 30 Hz
fig = plt.figure()
plt.plot(x, theta)
plt.plot(x, alpha)
plt.plot(x, beta)
plt.show()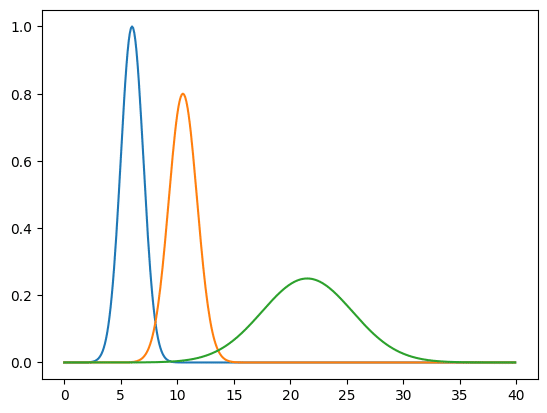
青がθ波、オレンジがα波、緑がβ波の分布です。
脳波のような波形を生成
分布ができたので、これを波形にしていきます。
基本は前にこちらの記事で紹介したランダムな波形を生成するプログラムです。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.5)
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()今回の分布は各波長の強度の分布なので、「hz_weight」に関数gaussで得られたリストを渡します。
それではそれぞれを見ていきましょう。
θ波
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()

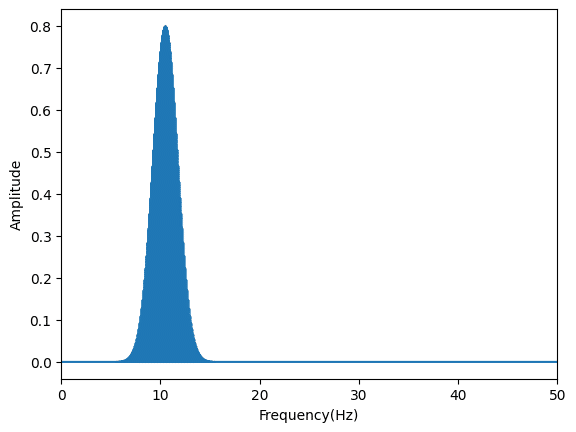
α波
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()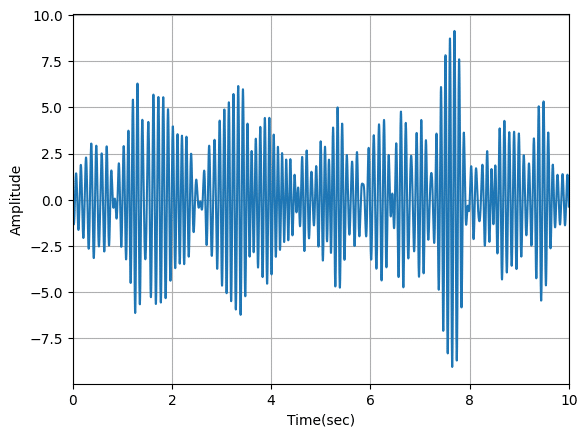
β波
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
hz_weight = gauss(hz_range, a=1/4, m=21.5, s=4) #13 - 30 Hz
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()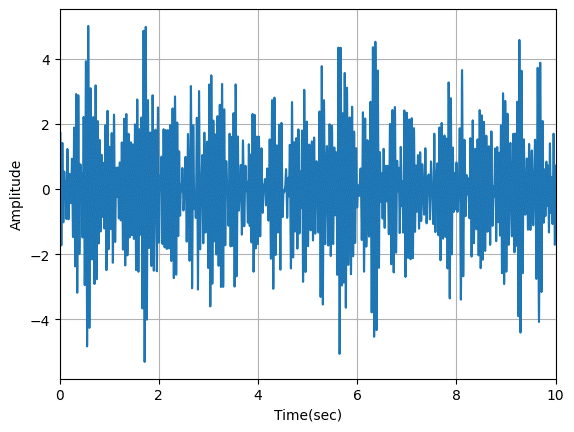
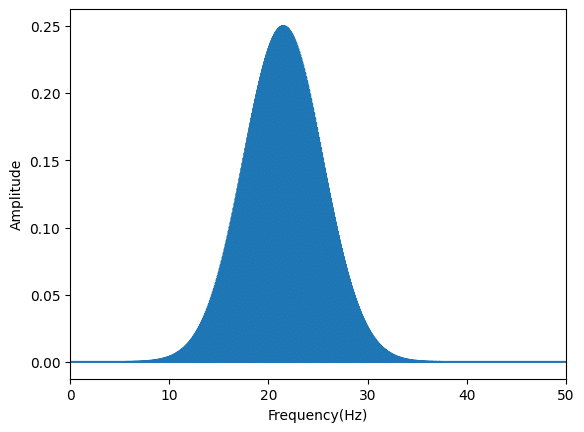
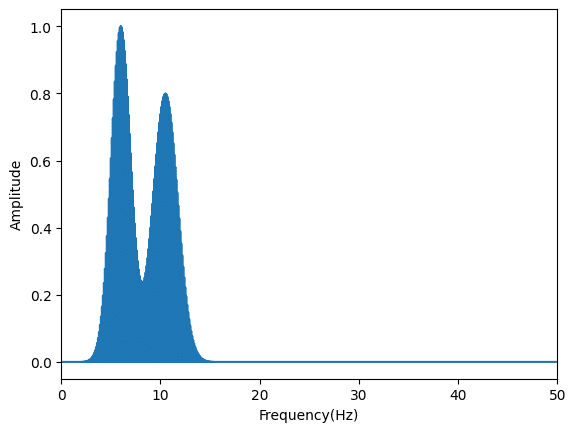
それぞれそれらしい波形と分布が得られました。
二つの帯域を合成する場合
次に二つの脳波、例えばθ波とα波が混ざったような波形を生成する方法です。
その場合はそれぞれの波形の周波数に対する強度を別々に作成し、波長ごとでたしあわせます。
ということでθ波とα波を合成する場合はこんな感じで強度のリストを作成します。
theta = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
alpha = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight = np.array(theta) + np.array(alpha)実際にプログラムを作成してみるとこんな感じです。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.1)
theta = gauss(hz_range, a=1/1, m=6, s=1) #4 - 8 Hz
alpha = gauss(hz_range, a=1/1.25, m=10.5, s=1.25) # 8 - 13 Hz
hz_weight = np.array(theta) + np.array(alpha)
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,50)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()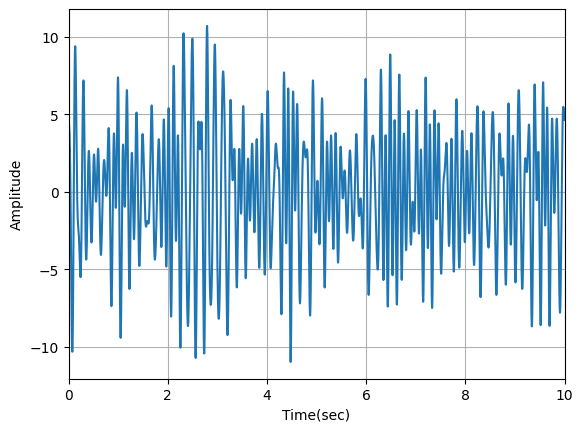
次回はこれらの波形を使って、波形を時間で変化させる方法を紹介します。

ではでは今回はこんな感じで。

コメント