目次
再帰処理
前回、PythonのMatplotlibでadd_subplotを使って複数のグラフを一括で表示する方法を紹介しました。
あわせて読みたい

【matplotlib】add_subplotを使って複数のグラフを一括で表示する方法[Python]
Matplotlib 前回、PythonのMatplotlibで指数表記になってしまった軸のラベルを整数表記に戻す方法と強制的に指数表記にする方法を紹介しました。 今回はMatplotlibでadd…
今回は再帰処理を使って面積を指定したガウス分布を作成する方法を紹介します。
まずガウス分布ですが、こちらの記事で使用した関数を使っていきます。
あわせて読みたい


【Python】正規分布(ガウス分布)を使い、脳波のα波、β波、θ波のような波形を作成してみた
正規分布 前回、NumpyのFFT(高速フーリエ変換)を使って周波数解析をする方法を紹介しました。 今回はPythonで正規分布(ガウス分布)のデータを作成する方法を紹介し…
とりあえずガウス分布を描いてみるプログラムを作成するとこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.show()
実行結果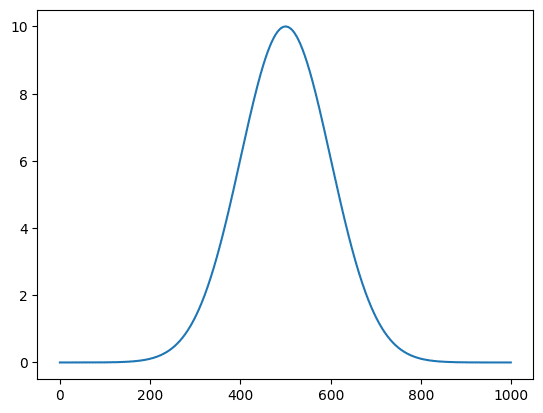
面積を求める方法
まずはこのガウス関数の面積を求める必要があります。
とは言っても単純に全ての値を足し算すれば面積が求まります。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
x_list = range(0, 1000)
y_param = [10, 500, 100]
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
y_area = sum(y_list)
print(y_area)
実行結果
2506.6268372625827面積を指定したガウス分布を作成する方法
次に面積を指定したガウス分布を作成する方法です。
今回、再帰処理の終了条件として、再帰処理の回数が一定数となった場合以外に、ガウス分布の面積が指定した値以下になった時というもう一つの条件を与えます。
そして今回の場合はガウス分布のパラメータのうち、ピーク高さである「a」の値を少しずつ小さくしつつ面積を計算し、指定した値と比較して、再帰処理を終了するかどうか判断します。
ということで再帰処理の関数はこんな感じになります。
def target_area(n, x_list, a, m, s, target, delta):
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
if n == 0:
return "no answer..."
elif y_area <= target:
return a
new_a = target_area(n-1, x_list, a-delta, m, s, target, delta)
return new_a再帰処理の関数の最初に得られたパラメータからガウス分布を作成し、面積を計算します。
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)再帰処理終了のための条件分岐は2つで、再帰処理の回数が指定した回数となった時、そしてガウス分布の面積が指定した値以下となった時です。
if n == 0:
return "no answer..."
elif y_area <= target:
return aここで終了しなかった場合、再帰処理の回数を減らした上、さらに今回はガウス分布のピーク高さのパラメータである「a」を少し減らして、次の処理を行います。
new_a = target_area(n-1, x_list, a-delta, m, s, target, delta)あとはグラフとして表示させる部分を追加して完了です。
import numpy as np
import matplotlib.pyplot as plt
x_list = range(0, 1000)
y_param = [10, 500, 100]
n = 10000
target = 500
delta = 0.01
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
def target_area(n, x_list, a, m, s, target, delta):
y_list = gauss(x_list, a, m, s)
y_area = sum(y_list)
# print(a, y_area)
if n == 0:
return "no answer..."
elif y_area <= target:
return a
new_a = target_area(n-1, x_list, a-delta, m, s, target, delta)
return new_a
new_a = target_area(n, x_list, y_param[0], y_param[1], y_param[2], target, delta)
original_y_list = gauss(x_list, y_param[0], y_param[1], y_param[2])
new_y_list = gauss(x_list, new_a, y_param[1], y_param[2])
y_area = sum(new_y_list)
fig = plt.figure()
plt.clf()
plt.plot(x_list, original_y_list)
plt.plot(x_list, new_y_list)
plt.show()
実行結果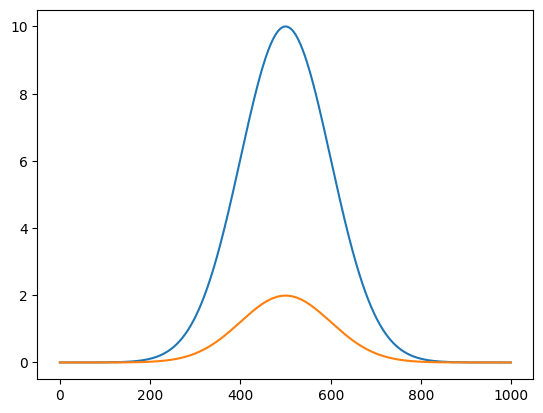
次回は今回の再帰処理を使って、再帰処理の回数を大幅に減らす方法を紹介します。
ではでは今回はこんな感じで。

コメント