機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnのボストンの住宅価格を予想するのにRidgeRegressionモデルとSVRモデルを使って機械学習してみました。
しかしどのモデルもLinearRegressionモデルと比べて、劇的に精度が向上するということは残念ながらありませんでした。
ということで、もう少し突っ込んんだことをしてみようというのが今回の内容。
その突っ込んだ内容というのが、データの標準化と正規化です。
標準化と正規化の必要性を解説するために、まずはいつものボストン住宅価格のデータセットを表示させてみましょう。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
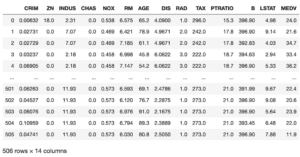
df
実行結果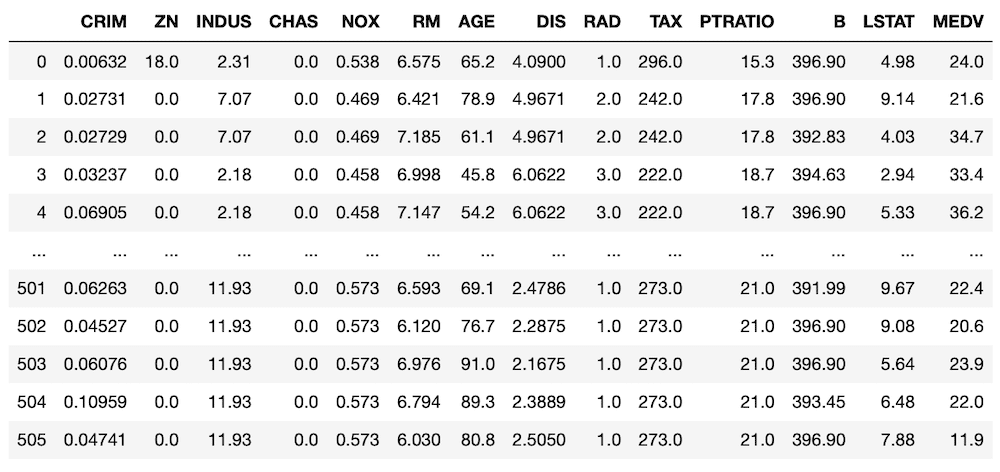
この中で今よく使っているのは、「CRIM」、「RM」、「LSTAT」の3つです。
その3つを眺めてみると「CRIM」は0.00632など小数点以下の値がぱっと見で目につきます。
対して「RM」や「LSTAT」は6.575や4.98など1より大きい少数が多いようです。
それぞれの最大値、最小値を表示してみましょう。
<セル2>
print(max(df["CRIM"]), min(df["CRIM"]))
print(max(df["RM"]), min(df["RM"]))
print(max(df["LSTAT"]), min(df["LSTAT"]))
実行結果
88.9762 0.00632
8.78 3.561
37.97 1.73CRIMの最大値は88.9762、最小値は0.00632。
RMの最大値は8.78、最小値は3.561。
LSTATの最大値は37.97、最小値は1.73。
こう見たときにまず問題の一つが、それぞれの値の桁数が違うので、同じように機械学習のデータとして用いたときに、意図しない「重み(偏り)」が生まれてしまうことです。
例えばCRIMの最大値は他の2つの値と比べて大きくなっています。
これを同等に扱ってしまうと、RMやLSTATのデータの価値が低く見積もられてしまう可能性があるということです。
もう一つの問題が、データのばらつき方が違うということです。
例えばCRIMのデータは最初表で見てみたときに、小数点以下の値ばかりでした。
ということは最大値である「88.9762」という値は他の値からみると飛び抜けた値かもしれないわけです。
その飛び抜け方はデータによってまちまちなので、やはり意図しない「重み(偏り)」が生じる原因となります。
ということで値やばらつきが違うデータを同じ土俵に乗せてやる処理が必要になります。
その処理というのが、「標準化」や「正規化」というわけです。
標準化(Standardization)、正規化(Normalization)
ということで標準化、正規化を試していきたいのですが、まずはそれぞれがどんな操作なのか簡単に解説していきましょう。
まず標準化(Standardization)ですが、これは「平均値を0として、標準偏差を1とする」方法です。
こうすることにより、データのばらつきの大きさに依存したデータに変換することができます。
正規化というのは定義があいまいなのですが、よく使われるのは「最大値を1に最小値を0にする」といった処理です。
要するにどこかに基準をおいて、データを変換するというのが正規化にというようです。
詳しく計算式など知りたい方は、こちらのサイトをご覧ください。

なかなか文章だけでは分かりにくいと思いますので、まずは標準化、正規化したデータをみてもらいましょう。
プログラムは後で記載しますので、まずはどんな感じになるのかを掴んでみてください。
ボストン住宅価格のLSTAT(低所得者の割合)のデータを何もしていないデータ(None)と標準化したデータ(Standardied)、正規化したデータ(Normalized)の3種類のデータを使ってグラフを描いてみます。
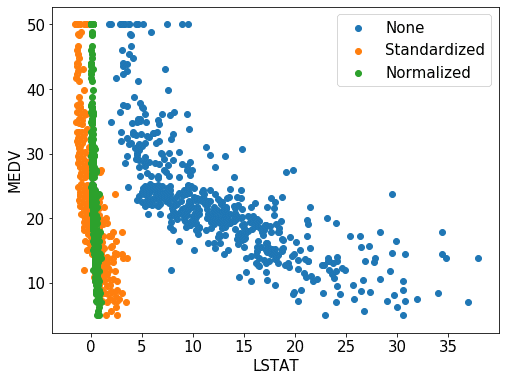
何もしていないデータ(None:青色の点)に比べると、標準化したデータ(Standardized:橙色の点)と正規化したデータ(Normalized:緑色の点)は0近くに集まっているのが分かります。
さらに0付近を拡大してみるとこんな感じです。
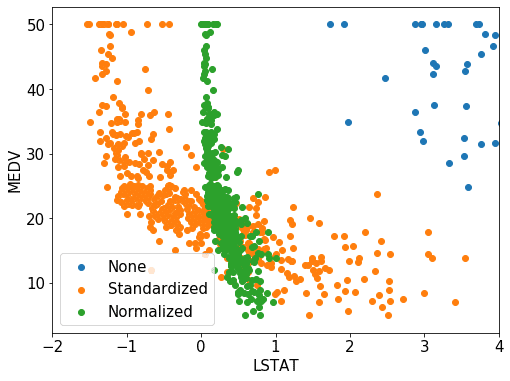
標準化したデータ(Standardized:橙色の点)は0を中心に左右に広がっていますが、正規化したデータ(Normalized:緑色の点)は0から1の間に全てのデータが集まっています。
ボストン住宅価格のCRIM(犯罪率)、RM(平均部屋数)、LSTAT(低所得者の割合)のデータを一つのグラフにして、それぞれ何もしていないデータと標準化したデータ、正規化したデータのグラフを描いてみます。
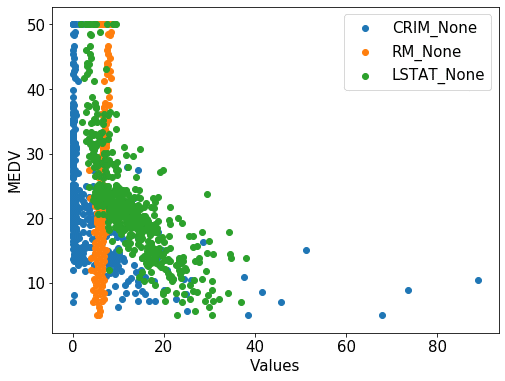
まずは何もしていないデータ。
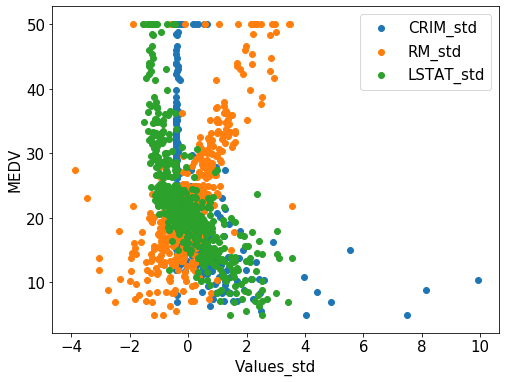
次に標準化したデータ。
最後に正規化したデータ。
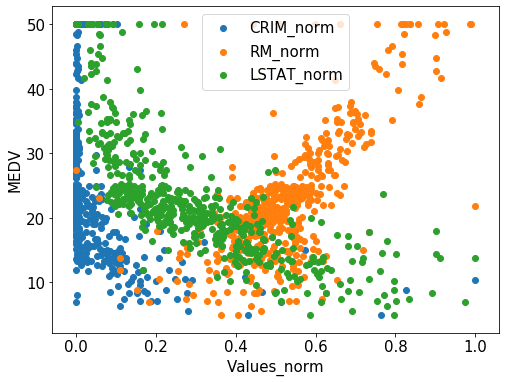
何もしていないデータでは、CRIM(青色)とRM(橙色)の点の広がり方が全く違っていたのに対し、標準化や正規化したデータでは同じような広がり方をしています。
このようにして違う性質(桁数だったり、広がり方だったり)をもつデータを同じように扱えるようにする処理が標準化だったり、正規化というわけです。
プログラムの解説:標準化、正規化
それでは標準化、正規化を比較したグラフを書くプログラムを解説していきます。
まずはライブラリのインポートです。
標準化、正規化のために「sklearn.preprocessing」の「StandardScaler」と「MinMaxScaler」をインポートします。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler次にボストン住宅価格のデータセットのうち、使うデータのみ変数に格納します。
xには「CRIM(犯罪率)」、「RM(平均部屋数)」、「LSTAT(低所得者の割合)」を格納し、yに「MEDV(住宅価格)」を格納しました。
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]次にデータを標準化していきます。
標準化のコマンドもこれまでやってきた機械学習のコマンドと似ていて、まずはモデルの読み込み「std_model = StandardScaler()」、そして処理「x_std = std_model.fit_transform(x)」となります。
std_model = StandardScaler()
x_std = std_model.fit_transform(x)次は正規化です。
正規化も標準化と同様、モデルを読み込み、処理をするという形です。
norm_model = MinMaxScaler()
x_norm = norm_model.fit_transform(x)標準化と正規化したデータを扱いやすいようにPandasのデータフレームに格納します。
std = pd.DataFrame(x_std, columns=["CRIM_std", "RM_std", "LSTAT_std"])
norm = pd.DataFrame(x_norm, columns=["CRIM_norm", "RM_norm", "LSTAT_norm"])まずはここまででまとめてみましょう。
<セル2>
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
std_model = StandardScaler()
x_std = std_model.fit_transform(x)
norm_model = MinMaxScaler()
x_norm = norm_model.fit_transform(x)
std = pd.DataFrame(x_std, columns=["CRIM_std", "RM_std", "LSTAT_std"])
norm = pd.DataFrame(x_norm, columns=["CRIM_norm", "RM_norm", "LSTAT_norm"])
実行結果
実行しても特に何も出てきませんが、エラーが出てこなければ大丈夫でしょう。
プログラムの解説:グラフ表示
次はそれぞれのデータをグラフ表示していきます。
今回は「matplotlib」を使うので、「from matplotlib import pyplot as plt」としてインポート、そしてグラフ表示のためのマジックコマンド「%matplotlib inline」を忘れずに。
from matplotlib import pyplot as plt
%matplotlib inline最初は「LSTAT(低所得者の割合)」の何もしていないデータ、標準化したデータ、正規化したデータのグラフです。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["LSTAT"], y, label="None")
plt.scatter(std["LSTAT_std"], y, label="Standardized")
plt.scatter(norm["LSTAT_norm"], y, label="Normalized")
plt.tick_params(labelsize=15)
plt.xlabel("LSTAT", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)「fig = plt.figure(figsize=(8,6))」でグラフを表示する画面の作成。
「plt.clf()」で一旦グラフ表示画面をクリアします。
そして「plt.scatter(x, y, label=”Name”)」でそれぞれのデータをプロットしていきます。
ここでは何もしていないデータ「df[“LSTAT”]」、標準化したデータ「std[“LSTAT_std”]」、正規化したデータ「norm[“LSTAT_norm”]」の3種類をプロットしています。
plt.scatter(df["LSTAT"], y, label="None")
plt.scatter(std["LSTAT_std"], y, label="Standardized")
plt.scatter(norm["LSTAT_norm"], y, label="Normalized")「plt.tick_params(labelsize=15)」で軸の数値のフォントサイズを「15」に。
「plt.xlabel(“LSTAT”, fontsize=15)」でX軸名を「LSTAT」にして、フォントサイズを「15」に。
「plt.ylabel(“MEDV”, fontsize=15)」でY軸名を「MEDV」にして、フォントサイズを「15」に。
最後に「plt.legend(fontsize=15)」で凡例を表示して、フォントサイズを「15」にしています。
次に同じデータですが、X軸方向に拡大したグラフを表示するのはこうなります。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["LSTAT"], y, label="None")
plt.scatter(std["LSTAT_std"], y, label="Standardized")
plt.scatter(norm["LSTAT_norm"], y, label="Normalized")
plt.tick_params(labelsize=15)
plt.xlabel("LSTAT", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
plt.xlim(-2,4)違うのは最後の1行。
「plt.xlim(-2,4)」とすることで、表示するX軸の範囲を設定しています。
次は同様にして「CRIM(犯罪率)」、「RM(平均部屋数)」、「LSTAT(低所得者の割合)」の何もしていないデータを同じグラフにプロット。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["CRIM"], y, label="CRIM_None")
plt.scatter(df["RM"], y, label="RM_None")
plt.scatter(df["LSTAT"], y, label="LSTAT_None")
plt.tick_params(labelsize=15)
plt.xlabel("Values", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)さらに同様にして「CRIM(犯罪率)」、「RM(平均部屋数)」、「LSTAT(低所得者の割合)」の標準化したデータを同じグラフにプロット。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(std["CRIM_std"], y, label="CRIM_std")
plt.scatter(std["RM_std"], y, label="RM_std")
plt.scatter(std["LSTAT_std"], y, label="LSTAT_std")
plt.tick_params(labelsize=15)
plt.xlabel("Values_std", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)さらにさらに同様にして「CRIM(犯罪率)」、「RM(平均部屋数)」、「LSTAT(低所得者の割合)」の正規化したデータを同じグラフにプロット。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(norm["CRIM_norm"], y, label="CRIM_norm")
plt.scatter(norm["RM_norm"], y, label="RM_norm")
plt.scatter(norm["LSTAT_norm"], y, label="LSTAT_norm")
plt.tick_params(labelsize=15)
plt.xlabel("Values_norm", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)全部合わせてみるとこんな感じです。
<セル3>
from matplotlib import pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["LSTAT"], y, label="None")
plt.scatter(std["LSTAT_std"], y, label="Standardized")
plt.scatter(norm["LSTAT_norm"], y, label="Normalized")
plt.tick_params(labelsize=15)
plt.xlabel("LSTAT", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["LSTAT"], y, label="None")
plt.scatter(std["LSTAT_std"], y, label="Standardized")
plt.scatter(norm["LSTAT_norm"], y, label="Normalized")
plt.tick_params(labelsize=15)
plt.xlabel("LSTAT", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
plt.xlim(-2,4)
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(df["CRIM"], y, label="CRIM_None")
plt.scatter(df["RM"], y, label="RM_None")
plt.scatter(df["LSTAT"], y, label="LSTAT_None")
plt.tick_params(labelsize=15)
plt.xlabel("Values", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(std["CRIM_std"], y, label="CRIM_std")
plt.scatter(std["RM_std"], y, label="RM_std")
plt.scatter(std["LSTAT_std"], y, label="LSTAT_std")
plt.tick_params(labelsize=15)
plt.xlabel("Values_std", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(norm["CRIM_norm"], y, label="CRIM_norm")
plt.scatter(norm["RM_norm"], y, label="RM_norm")
plt.scatter(norm["LSTAT_norm"], y, label="LSTAT_norm")
plt.tick_params(labelsize=15)
plt.xlabel("Values_norm", fontsize=15)
plt.ylabel("MEDV", fontsize=15)
plt.legend(fontsize=15)
実行結果




これでグラフが表示できました。
これで標準化、正規化というのが何となく分かってもらえたでしょうか?
また特に複数の数値データを使って機械学習させていくときには、画一化したデータにするために重要だということも理解してもらえたらいいなと思います。
さてさて次回は標準化や正規化したデータを使って、機械学習させてみて、どれくらい予測精度が変わってくるのかを試してみたいと思います。
ということで今回はこんな感じで。

コメント