機械学習ライブラリScikit-learn
前回、機械学習における標準化(Standardization)と正規化(Normalization)を解説しました。
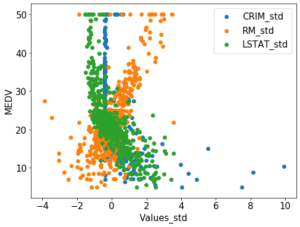
今回はボストンの住宅価格のデータセットを使って、標準化と正規化をすると予想の精度が良くなるのかということを試してみようと思います。
ということでいつも通り、まずはデータセットの読み込みから。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
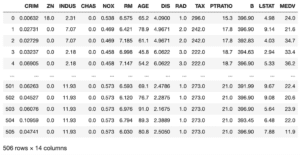
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果
必要な特徴量(CRIM、RM、LSTAT)のみ変数xに格納、さらに予想する対象となる住宅価格(MEDV)を変数yに格納します。
そして変数xを標準化して変数x_stdを、正規化して変数x_normを用意します。
<セル2>
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
std_model = StandardScaler()
x_std = std_model.fit_transform(x)
norm_model = MinMaxScaler()
x_norm = norm_model.fit_transform(x)ここまでで何もしていないデータ、標準化したデータ、正規化したデータが得られました。
LinearRegressionモデルで繰り返し検証プログラムを作成
これまでLinearRegressionモデル、Lassoモデル、ElasticNetモデル、RidgeRegressionモデル、SVRモデルと色々試してきましたが、今回は1番の基本のLinearRegressionモデルで効果を見てみましょう。
ということでインポートから。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as npデータを訓練用とテスト用に分割する「train_test_split」。
LinearRegressionモデル「LinearRegression」。
予想を評価するための決定関数「r2_score」。
ちょっと計算するための「numpy」。
まずはデータを訓練用とテスト用に分割していきます。
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
x_std_train, x_std_test, y_std_train, y_std_test = train_test_split(x_std, y, test_size=0.2, train_size=0.8)
x_norm_train, x_norm_test, y_norm_train, y_norm_test = train_test_split(x_norm, y, test_size=0.2, train_size=0.8)今回は残念ながら、何もしていないデータと標準化したデータ、正規化したデータで全く同じように分割はできません。
train_test_splitのオプションとして、乱数を固定する「random_state=X」というコマンドもあります。
しかし乱数を固定してしまうと毎回同じように分割され、同じ結果になり、それを繰り返し計算をしているだけになってしまいます。
ということで今回は「random_state=X」のオプションは無しでいきます。
そしてこれまで通り、モデルを変数に格納し、機械学習させ、予想します。
model_lr = LinearRegression()
model_std_lr = LinearRegression()
model_norm_lr = LinearRegression()
model_lr.fit(x_train, y_train)
model_std_lr.fit(x_std_train, y_std_train)
model_norm_lr.fit(x_norm_train, y_norm_train)
pred_lr = model_lr.predict(x_test)
pred_std_lr = model_std_lr.predict(x_std_test)
pred_norm_lr = model_norm_lr.predict(x_norm_test)今回は何もしていないデータ、標準化したデータ、正規化したデータがあるので、モデルは「model_lr」、「model_std_lr」、「model_norm_lr」の3種類を作りました。
そして機械学習後「.predict(テスト用データ)」でテスト用データに対する予想をし、それぞれ「pred_lr」、「pred_std_lr」、「pred_norm_lr」に格納しました。
あとはfor文を使って繰り返し、毎回計算した決定関数をリストに格納、平均値を計算、表示という流れになります。
全部書いてみるとこんな感じです。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np
trial = 100
pred_lr_score = []; pred_std_lr_score =[]; pred_norm_lr_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
x_std_train, x_std_test, y_std_train, y_std_test = train_test_split(x_std, y, test_size=0.2, train_size=0.8)
x_norm_train, x_norm_test, y_norm_train, y_norm_test = train_test_split(x_norm, y, test_size=0.2, train_size=0.8)
model_lr = LinearRegression()
model_std_lr = LinearRegression()
model_norm_lr = LinearRegression()
model_lr.fit(x_train, y_train)
model_std_lr.fit(x_std_train, y_std_train)
model_norm_lr.fit(x_norm_train, y_norm_train)
pred_lr = model_lr.predict(x_test)
pred_std_lr = model_std_lr.predict(x_std_test)
pred_norm_lr = model_norm_lr.predict(x_norm_test)
pred_lr_score.append(r2_score(y_test, pred_lr))
pred_std_lr_score.append(r2_score(y_std_test, pred_std_lr))
pred_norm_lr_score.append(r2_score(y_norm_test, pred_norm_lr))
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_std_lr_ave = np.average(np.array(pred_std_lr_score))
pred_norm_lr_ave = np.average(np.array(pred_norm_lr_score))
print(pred_lr_ave, pred_std_lr_ave, pred_norm_lr_ave)
実行結果
0.6251955895149124 0.6285481272482702 0.6384084236567933標準化と正規化は予測精度を向上させるのか?
プログラムも完成したことですし、いつも通り100回試行の決定関数の平均値を5回計算させてみます。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
| なし | 0.62520 | 0.64146 | 0.62304 | 0.62763 | 0.62896 |
| 標準化 | 0.62855 | 0.61883 | 0.63465 | 0.62859 | 0.62614 |
| 正規化 | 0.63841 | 0.63320 | 0.62716 | 0.62421 | 0.63256 |
ぱっと見てみたところ、標準化や正規化をしようがあまり変わらないという結果になってしまいました。
本音を言うと少しだけ上がってくれるんじゃないかと期待していたのですが、なかなか簡単にはいかないようです。
ここで考えられるのが、LinearRegressionでは標準化や正規化の影響は少ないのではないかということ。
つまり違うモデルだと標準化、正規化することで精度がよくなるのではないでしょうか。
ということで次回はLassoモデルとElasticNetモデルを使って、標準化、正規化の影響を見てみたいと思います。
ではでは今回はこんな感じで。

コメント