Apple Watch
前回、Apple Watchで取得した心電図データをPythonのMatplotlibを使ってグラフとして表示してみました。
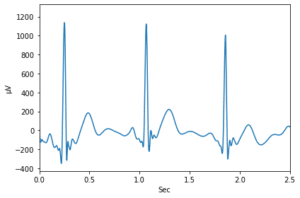
今回はさらに解析ということで、フーリエ変換し、どのような周波数成分が含まれているのか解析してみたいと思います。
フーリエ変換:Fourier Transform
フーリエ変換の詳細な解説に関しては、Wikipediaをご覧ください。
合っているか、間違っているか分かりませんが、私が理解しているフーリエ変換は「複数の周期成分(つまり繰り返し成分)が含まれるデータにおいて、どのような周期が含まれているのか分解する」手法です。
今回は心拍という安静時なら1分間に60〜90回、ほぼ定期的に同じ強度の振幅が含まれるデータなので、その心拍がどれくらいの周期、つまり一つの心拍から次の心拍までの間隔が何秒なのかを抽出することができます。
例えば前回グラフ化したデータですとこんな感じ。
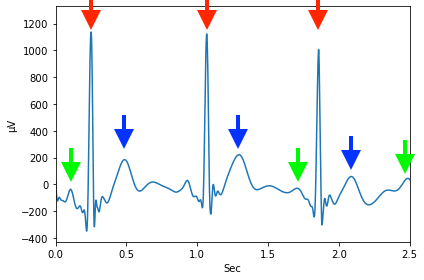
一番目立つのが赤の矢印のピークこれが何秒間隔で起きているのか?
この場合は見るからに他のピークと違い鋭いピークになっているので、見るだけでその間隔は掴むことができ、大体0.8秒程度の間隔のように見えます。
では青や緑の矢印のピークはどうでしょうか?
これも赤の矢印のように0.8秒程度の間隔のように見えますが、特に緑の矢印のピークに関しては他に似たようなピークが近くにあり、もしかしたらもっと速い間隔、つまり短い周期を持っているかもしれません。
これを明らかにするためにフーリエ変換をすることで、どんな周期の成分が含まれているか明確にしようというわけです。
今回の心拍のようなデータだけでなく、音声だったり、電磁波のような波のデータ、また結晶構造のように周期構造を持つデータなどに使用できるようです。
ちなみに数式に関してはさっぱり分かりません。
それでは始めていきましょう。
プログラムのおさらい
まずは前回作成した心電図データ(CSVファイル)の読み込み部分のおさらいです。
import os
import csv
import matplotlib.pyplot as plt
ecg_filename = 'ecg_example.csv'
default_dirpath = os.getcwd()
ecg_filepath = os.path.join(default_dirpath, ecg_filename)
print(default_dirpath)
print(ecg_filepath)
skiprows = 13
def ecgdataget():
data = []; samplerate = 512
with open(ecg_filepath, 'r', encoding='utf-8') as f_in:
ecg_file = csv.reader(f_in)
for i, row in enumerate(ecg_file):
if 'サンプルレート' in row:
samplerate = int(row[1].rstrip('ヘルツ'))
if i >= skiprows:
data.append(float(row[0]))
return data, samplerate
data, samplerate = ecgdataget()
print(samplerate)
print(data)
fig = plt.figure()
plt.clf()
plt.plot(time, data)
plt.xlabel('Sec')
plt.ylabel(u'\u03bcV')
plt.tight_layout()詳しい解説は前回の記事をご覧ください。

とりあえず現状としては、心電図のデータが「data」にリスト形式で格納されており、サンプルレートが「samplerate」に整数として格納されています。
この二つのデータを使ってフーリエ変換していきます。
NumpyによるFFT解析
ちなみにPC上で高速にフーリエ変換を行うアルゴリズムによる解析のことを高速フーリエ変換(Fast Foureir Transform)といい、よくFFT解析と略されています。
そしてPythonでいうとNumpyやSciPy等でFFT解析をすることができるようですが、今回は一番慣れ親しんでいるNumpyを使ってFFT解析していきましょう。
ということでプログラム全体としてはこんな感じ。
import numpy as np
N = len(data)
freq = np.fft.fftfreq(N, d=1/samplerate)
F = np.fft.fft(data)
amp = np.abs(F/(N/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(N/2)], amp[1:int(N/2)])
plt.xlabel('Frequency[Hz]')
plt.ylabel('Amplitude')
plt.tight_layout()とりあえず最初にNumpyをインポートしています(import numpy as np)。
中盤(fig = plt.figure())から後半(plt.tight_layout())はグラフ表示部分です。
そしてFFT解析しているのはこちらの部分です。
N = len(data)
freq = np.fft.fftfreq(N, d=1/samplerate)
F = np.fft.fft(data)
amp = np.abs(F/(N/2))まずNはデータのサンプル数なので、「len(data)」で取得しています。
次にX軸となる周波数成分のリストを「np.fft.fftfreq(’サンプル数’, d=’周期’)」で作成します。
これを表示させてみるとこんな感じです。
print(freq)
実行結果
[ 0. 0.03333333 0.06666667 ... -0.1 -0.06666667
-0.03333333]次にFはフーリエ変換したデータですので、「np.fft.fft(‘フーリエ変換したいデータ’)」でフーリエ変換します。
ちなみにフーリエ変換したデータを見てみるとこんな感じです。
print(F)
実行結果
[-3479.695 +0.j -3261.89970162-1754.75410207j
-3002.11252775-3346.18864269j ... -2421.0932242 +5327.65481629j
-3002.11252775+3346.18864269j -3261.89970162+1754.75410207j]数値としては「-3479.695 +0.j」といった形になっていますが、このように「+ 数値 j」というのは複素数の虚部の部分です。
つまりその前の数字は複素数の実部です。
実はこのままではまだ使えないので、さらに振幅に変換します(amp = np.abs(F/(N/2)))。
ちなみにnp.abs()で絶対値に変換し、フーリエ変換後のデータFをサンプル数の半分で割っているようです。
単純に「np.abs(F)」としているサイトもありますが、サンプル数の半分、つまり定数で全データを割っているので、周波数の分布を見るのであれば、それほど大きな意味を持たない気もします。
数学的なことに関しては、間違っていることも多々あると思うので、詳しいことに関しては専門書を読み解いてください。
これでフーリエ変換のデータを取得することができました。
グラフ表示
そしてグラフ表示にいきますが、全体的には前回や前に解説したことなので省きます。
1箇所だけ補足します。
「plt.plot(freq[1:int(N/2)], amp[1:int(N/2)])」ですが、データの範囲を「1からサンプル数の半分」までとしています。
ちなみに実行するとこんなグラフが得られます。
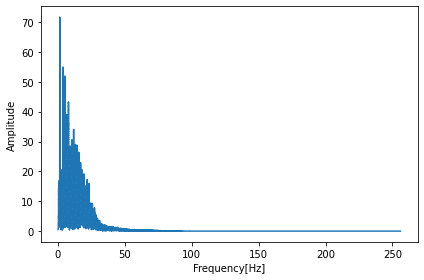
分かりづらいので25Hzまでの領域を拡大してみましょう(plt.xlim(0, 25)を追加)。
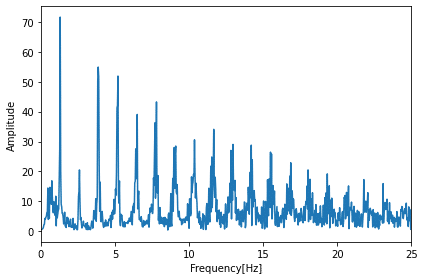
このデータでピークになっているところが、周波数として多いところになります。
ピークのうち0に近いピークの周波数は1.3Hzです。
つまり1秒間に1.3回このピークが現れるので、\(1.3 \times 60 = 78\)となり、1分間の心拍数は78回でほぼ合っている値になります。
とFFT解析がうまくいったのはいいですが、なぜグラフの表示が「1からサンプル数の半分」なのかの疑問ですが、一度全範囲の表示をしてみましょう。
import numpy as np
N = len(data)
F = np.fft.fft(data)
freq = np.fft.fftfreq(N, d=1/samplerate)
amp = np.abs(F/(N/2))
fig = plt.figure()
plt.clf()
plt.plot(freq, amp)
plt.xlabel('Frequency[Hz]')
plt.ylabel('Amplitude')
plt.tight_layout()
実行結果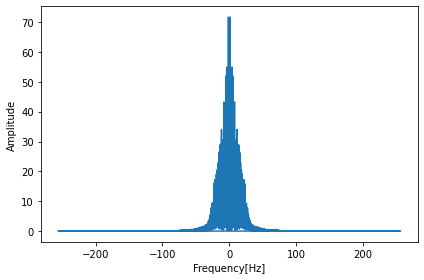
この結果を見てわかるように、あとは半分のデータは周波数がマイナス側のデータということがわかります。
ただ周波数は振幅の回数なので、プラスとマイナスは同じ意味合い(同じ振幅の値)を持ちます。
ということでプラス側だけ表示すれば良いということで、データ数の半分の領域になっているということです。
ではでは今回はこんな感じで。


コメント