t検定
前回、Streamlitのst.writeとst.textの違いを紹介しました。
今回はSciPyのstatモジュールを使ってt検定をしてみます。
t検定が何かというとWikipediaではこんな感じで説明されています。
t検定(ティーけんてい)とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらない(ただし自由度による)ことを利用している。
https://ja.wikipedia.org/wiki/T%E6%A4%9C%E5%AE%9A
このままではよくわからないのですが、ものすごく単純化して言うと「2つの集団に差があるかどうか」を数学的(統計的)に示す方法です。
もしちゃんと勉強したい方は専門のサイトなり、専門書なりで勉強してもらうことにして、とりあえずここではPythonでt検定ができるようにしていきたいと思います。
それでは始めていきましょう。
t検定に用いるデータ用のプログラム
まずは今回t検定で用いるデータ用のプログラムを作成していきましょう。
データにはある程度の分布が必要なため、前に作成したガウス分布のプログラムを使っていきましょう。

ということでこんな感じで2つの集団(y1、y2)を作成してみました。
import numpy as np
import matplotlib.pyplot as plt
import random
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(0, 100, 1)
w1 = gauss(x, m=60)
w2 = gauss(x, m=80)
y1 = random.choices(x, k=100, weights=w1)
y2 = random.choices(x, k=100, weights=w2)
fig = plt.figure()
plt.hist(y1)
plt.hist(y2)
plt.xlim(0, 100)
plt.show()「x = np.arange(0, 100, 1)」で0から100のリストを作ります。
そして1つ目の集団を作成するための確率分布として「w1 = gauss(x, m=60)」を、2つ目の集団を作成するための確率分布として「w2 = gauss(x, m=80)」として、ガウス分布に従う確率分布を2つ作成します。
その確率分布を使って、ランダムに値を取得し、2つの集団を作成しました(y1 = random.choices(x, k=100, weights=w1)、y2 = random.choices(x, k=100, weights=w2))。
最後にmatplotlibのhist(ヒストグラム)を使って、作成した集団の分布グラフを作成しました。
できたグラフはこんな感じ。
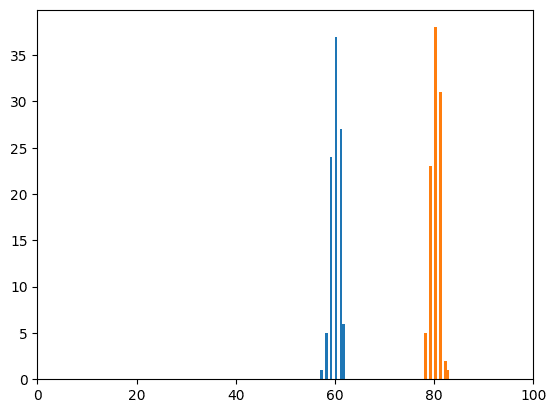
0から100にしたのは0点から100点のテストを想定していて、random.choicesでk=100としたのは100人の学生が試験を受けたときの各学生の得点を取得しているというわけです。
こんな感じの分布を使ってt検定をしてみましょう。
SciPyのstatモジュールを使ったt検定
それではSciPyのstatモジュールを使ったt検定をしていきます。
今回は2つの集団の間に対応がない(違う集団)、正規分布に従うといった条件の際に用いるWelchのt検定を行ってみます。
最終的にはp値という値が得られ、この値によって2つの集団の間に差があるかどうかを検討します。
p値を算出するには「stats.ttest_ind(集団1, 集団2, equal_var=False).pvalue」とします。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(0,100, 1)
w1 = gauss(x, m=60)
w2 = gauss(x, m=80)
y1 = random.choices(x, k=100, weights=w1)
y2 = random.choices(x, k=100, weights=w2)
fig = plt.figure()
plt.hist(y1)
plt.hist(y2)
plt.xlim(0, 100)
plt.show()
print(stats.ttest_ind(y1, y2, equal_var=False).pvalue)
実行結果
5.677953405330379e-197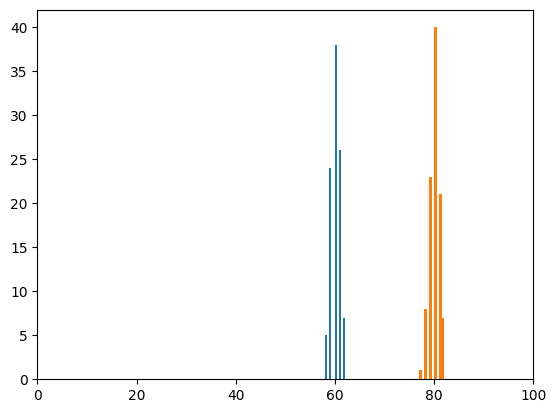
p値がどれくらいになったら差があると言えるかはその時々で少し変わることがありますが、通常5%、つまり0.05より小さければ2つの集団には差があるとすることが多いです。
今回は「5.677953405330379e-197」というものすごく小さな値になったので、この2つの集団には差があるといえるでしょう。
ついでに逆にp値が5%よりも大きくなる場合も見てみましょう。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_list
x = np.arange(0,100, 1)
w1 = gauss(x, m=80)
w2 = gauss(x, m=80)
y1 = random.choices(x, k=100, weights=w1)
y2 = random.choices(x, k=100, weights=w2)
fig = plt.figure()
plt.hist(y1)
plt.hist(y2)
plt.xlim(0, 100)
plt.show()
print(stats.ttest_ind(y1, y2, equal_var=False).pvalue)
実行結果
0.3480059190355872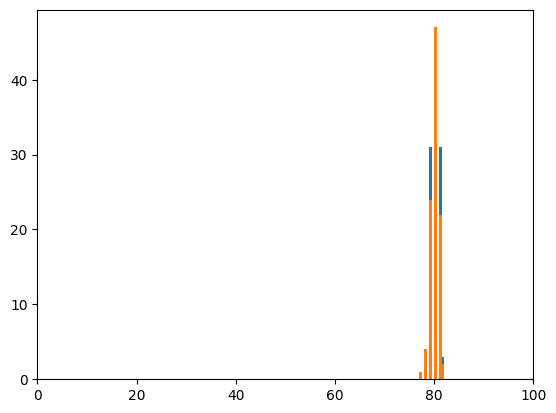
同じ分布にしてみたところ、p値が「0.3480059190355872」となりました。
この場合は「差がない」とは言えず、「差があるかどうかは分からない」と言うのが正しい解釈とのことです。
ここら辺の解釈に関しても専門のサイトや専門書で勉強したもらう方が正しいのでここでは割愛します。
次回はmatplotlibで図形を描く方法を紹介します。
ではでは今回はこんな感じで。

コメント