機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnのボストンの住宅価格と他の特徴量をグラフにして、どの特徴量が関連しているのか検討しました。
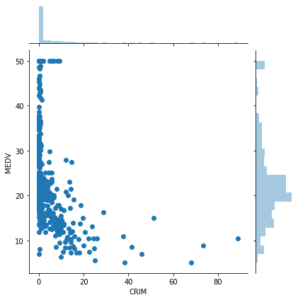
その結果では、高い関連性があるのは、こちらの3つでした。
- 犯罪率(CRIM)
- 平均部屋数(RM)
- 低所得者の割合(LSTAT)
また関連がありそうだというのはこちらの3つでした。
- 広い住宅区画の割合(ZN)
- 小売業以外のビジネスがされている土地の割合(INDUS)
- 窒素酸化物の濃度(NOX)
ということでここら辺のデータを使って機械学習させ、ボストンの住宅価格を予想し、その結果を評価してみようというのが今回の内容です。
まずはデータを読み込んで、準備をしましょう。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果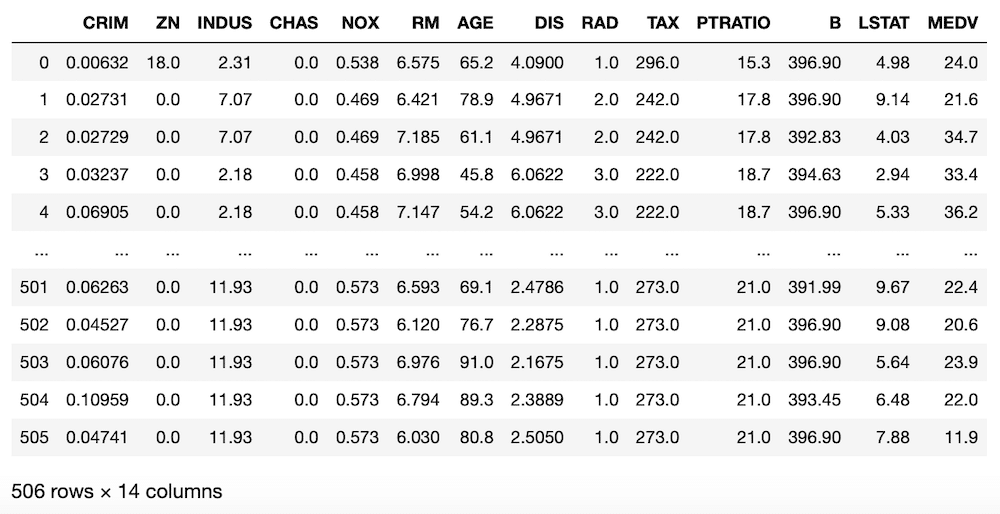
訓練用データとテスト用データに分割
まずは機械学習に使う特徴量だけ変数x、yに格納して、訓練用データとテスト用データに分割していきましょう。
最初はこちらの3つの特徴量で機械学習を行なってみましょう。
- 犯罪率(CRIM)
- 平均部屋数(RM)
- 低所得者の割合(LSTAT)
これら3つを変数xに、予想する値である住宅価格を変数yに格納します。
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]そして「train_test_split」を使って、データを訓練用データとテスト用データに分割します。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)この2つのプログラムを合わせて、最後にそれぞれのデータのサイズを表示してみます。
<セル2>
from sklearn.model_selection import train_test_split
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
print(len(x_train), len(x_test), len(y_train), len(y_test))
実行結果
404 102 404 102もともと全体として506個のデータがあり、8割を訓練用データ(train_size=0.8)、2割をテスト用データ(test_size=0.2)としているので、訓練用データは404個、テスト用データは102個で合っていますね。
ということでデータを分割することができました。
線形回帰(Linear Regression)とは?
前にiris(アヤメ)の分類を行った時は、SVM(サポートベクターマシン)という分類を行うための機械学習モデルを用いました。
今回は分類をしたいわけではなく、ある条件の住宅の価格を予想したいということで、回帰(Regression)というモデルを使います。
回帰を今回のデータを用いて説明すると、例えば犯罪率と住宅の価格には関連性がありました。
それは住宅の価格が高くなると、犯罪率が低くなるというものでした。
そこで犯罪率と住宅の価格の関係性を数式とすることが回帰(もしくは回帰分析)で、できた数式が回帰式です。
このようにxを1つ、yを1つで回帰式を作るのを「単回帰分析」、xが2つ以上、yが1つで回帰式を作るのを「重回帰分析」といいます。
またその回帰式が直線の場合は「線形回帰(Linear regression)」、曲線の場合は「非線形回帰(Non-linear regression)」となります。
私が理解していることを、大まかに解説してみましたが、もっと詳しく知りたい方はご自分で調べてみてください。
今回は「犯罪率」、「平均部屋数」、「低所得者の割合」の3つを使うので重回帰分析です。
また回帰式を直線とする「線形回帰」を使ってみましょう。
線形回帰モデルを使って機械学習
Scikit-learnの線形回帰モデル(Linear Regression)を使用するには、まずはモデルのインポートが必要になります。
from sklearn.linear_model import LinearRegression機械学習させる方法はSVM(サポートベクターマシン)を使った時と同様です。
model = LinearRegression()
model.fit(x_train, y_train)とすることでモデルを決定し、機械学習をさせることができます。
そしてテストデータを使って、住宅価格を予想させるのも同じです。
ということでここまでをまとめてみるとこんな感じ。
<セル3>
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(y_pred)
実行結果
[20.78955514 29.27476045 30.48163258 21.09758014 21.1901468 30.50526733
18.28901593 35.57862372 22.10217807 22.10107328 17.71816556 26.7754292
19.04169421 20.3779374 35.24033005 18.76414184 16.53819036 20.68638404
16.93828298 17.97753394 26.2870573 16.40361813 30.46544387 37.14450504
8.40605067 25.93035242 18.76857237 27.57076017 34.80511347 18.4986455
(以下略)出てきた数字がそれぞれのデータから予想された住宅価格です。
ここまではSVM(サポートベクターマシン)の時と同じなのですが、評価のコマンドは違います。
ちなみに前に使った「accuracy_score」を使ってみるとこんな感じ。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import accuracy_score
model = LinearRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
accuracy_score(y_test, y_pred)
実行結果
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-13-2a2caf3a24e4> in <module>
6
7 y_pred = model.predict(x_test)
----> 8 accuracy_score(y_test, y_pred)
/opt/anaconda3/lib/python3.7/site-packages/sklearn/metrics/classification.py in accuracy_score(y_true, y_pred, normalize, sample_weight)
174
175 # Compute accuracy for each possible representation
--> 176 y_type, y_true, y_pred = _check_targets(y_true, y_pred)
177 check_consistent_length(y_true, y_pred, sample_weight)
178 if y_type.startswith('multilabel'):
/opt/anaconda3/lib/python3.7/site-packages/sklearn/metrics/classification.py in _check_targets(y_true, y_pred)
86 # No metrics support "multiclass-multioutput" format
87 if (y_type not in ["binary", "multiclass", "multilabel-indicator"]):
---> 88 raise ValueError("{0} is not supported".format(y_type))
89
90 if y_type in ["binary", "multiclass"]:
ValueError: continuous is not supported最後に出てきた「continuous is not supported」というのは「連続した値はサポートしていません」ということのようです。
ということで次に線形回帰モデルを使った際の評価の方法を解説していきます。
決定係数:R2
線形回帰モデルで使う評価の指標としては、決定係数(R2 アール二乗)というものがあります。
この値は1に近ければ機械学習で得られた予想と本当の答えが一致していて、0に近いと一致していないという値になります。
他にも評価の値があるのですが、そちらはまた今度ということにして、今回は決定係数を使って進めていきます。
この決定係数を使う場合は、このコマンドをインポートする必要があります。
from sklearn.metrics import r2_scoreそして「r2_score(答え、予想)」とすることで決定係数を計算することができます。
ということで先ほどの<セル3>はこんな感じになります。
<セル3 変更>
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
model = LinearRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
r2_score(y_test, y_pred)
実行結果
0.6321961183215488今回は「0.632196…」ということで、そこまで1に近くないですが、0にも近くないという中途半端な値でした。
これだと傾向としては捉えられているが、値がぴったり合っているわけではないという感じでしょうか。
今回はとりあえず線形回帰モデルで機械学習できたということでここまでにしておきたいと思います。
次回はさらに関連性がありそうな3つの特徴量を加え、決定係数が1に近くか試していきたいと思います。
ではでは今回はこんな感じで。

コメント