FFT(高速フーリエ変換)
前回、Pythonでランダムな波形を作成する方法を紹介しました。

せっかく波形を作成したので、FFT(高速フーリエ変換)して、周波数解析をしてみましょう。
私の知識としてはとりあえずFFTをすれば、波の周波数解析ができるくらいのものなので、しっかり理論から学びたい方はこちらのサイト等で勉強してください。
ちなみに前に「Apple Watchで取得した心電図データを周波数解析」ということもしていますので、よかったらどうぞ。
それでは始めていきましょう。
ランダムな波形を作成するプログラム
まずは前回のランダムな波形を作成するプログラムのおさらいです。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.5)
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fig = plt.figure()
plt.clf()
plt.plot(df["Time"], df["SUM"])
plt.grid()
plt.xlabel("Time(sec)")
plt.ylabel("Amplitude")
plt.xlim(0, 10)
plt.show()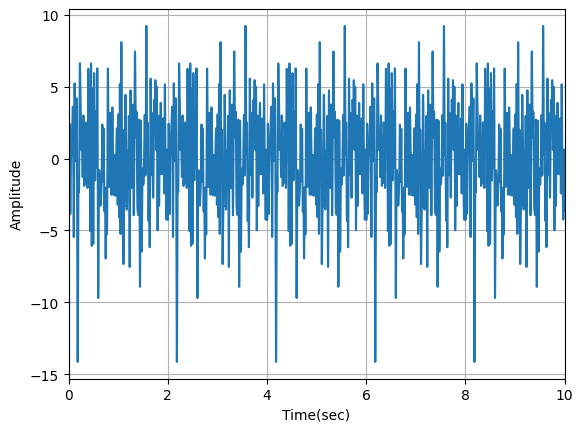
この状態でdf[“Time”]に時間が、df[“SUM”]に強度が格納されています。
NumPyでFFT
NumPyを用いてFFT解析をするには、時間に対する信号の強度(波のデータ、今回だとdf[“SUM”])とデータ数、サンプリングレート(今回だとsamplingrate)が必要です。
先ほどのプログラム内に両方とも含まれていますので、それらを用いてFFT解析を行います。
fft_data = np.fft.fft(波のデータ)
freq = np.fft.fftfreq(len(波のデータ), 1/サンプリングレート)
Amp = abs(fft_data/(len(波のデータ)/2))まず「np.fft.fft(波のデータ)」を用いてFFT解析を行い、ピーク強度を取得します。
そして「np.fft.fftfreq(データ数, 1/サンプリングレート)」で周波数のデータを取得します。
最後にFFT解析の結果は複素数で得られ、実数部分のみが必要であるため「abs」で絶対値を取得しますが、その際、振幅を計算するため、ピーク強度を「データ数/2」で割ります。
X軸に周波数「freq」、Y軸に振幅「Amp」をプロットすると、FFTによる周波数解析の結果が得られます。
ということでこんな感じ。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = np.arange(0, 40, 0.5)
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,100)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()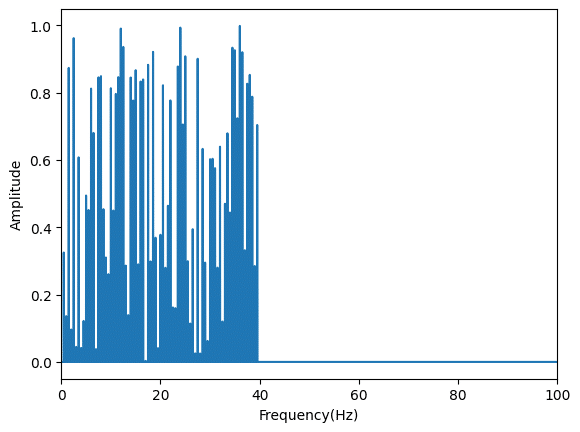
ちなみに解析できる周波数はサンプリングレートの半分まで、つまり今回の場合、サンプリングレートが1000 Hzであるため、解析できる周波数は500 Hzまでです。
ただ今回の波形の中には40 Hzまでの波しか入っていないので、表示範囲を「0 〜 100 Hz」としています。
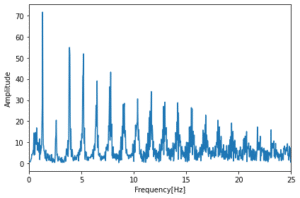
すると40 Hzまでのところにさまざまな高さのピークがみられ、複数の周波数が含まれていることが分かります。
もっと単純化するために10 Hz、20 Hz、30 Hz、40 Hz、50 Hzを含んだ波形にしてみましょう。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
time = 60
samplingrate = 1000
hz_range = [10, 20, 30, 40, 50]
hz_weight = [0 for _ in hz_range]
data_list = [np.arange(0, time, 1/samplingrate)]
for hz, w in zip(hz_range, hz_weight):
if w == 0:
weight = random.random()
else:
weight = w
fai = random.random() * 2*np.pi
data_list.append(weight * np.sin(2*np.pi*hz*data_list[0] + fai))
columnnames = [hz for hz in hz_range]
columnnames.insert(0, "Time")
df = pd.DataFrame(data_list).transpose()
df = df.set_axis(columnnames, axis="columns")
df["SUM"] = df.iloc[:, 1:].sum(axis=1)
fft_data = np.fft.fft(df["SUM"])
freq = np.fft.fftfreq(len(df["SUM"]), 1/samplingrate)
Amp = abs(fft_data/(len(df["SUM"])/2))
fig = plt.figure()
plt.clf()
plt.plot(freq[1:int(len(df["SUM"])/2)], Amp[1:int(len(df["SUM"])/2)])
plt.xlim(0,100)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude")
plt.show()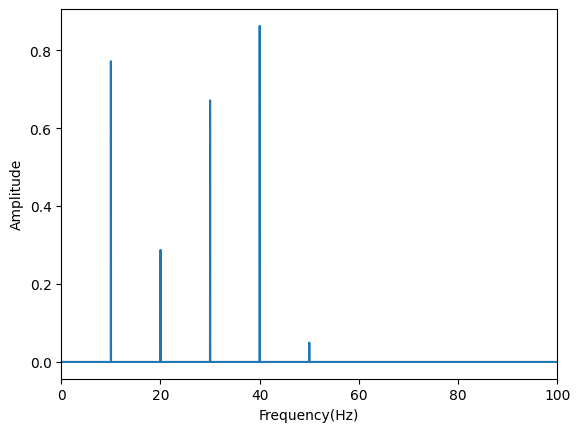
10 Hz、20 Hz、30 Hz、40 Hz、50 Hzにピークが見られ、ちゃんと周波数解析ができていることが分かります。
次回はPythonで正規分布(ガウス分布)を使い、脳波のα波、β波、θ波のような波形を作成してみましょう。

ではでは今回はこんな感じで。

コメント