目次
SciPy
前回、PythonのPandasでデータフレームからデータを抽出し、concatを使って連結させる場合に注意することを紹介しました。
あわせて読みたい
【Pandas】データフレームからデータを抽出し、concatを使って連結させる場合に注意すること[Python]
Pandas 前回、PythonのPandasで行名や列名を一括で変更する方法を紹介しました。 今回はPandasでデータフレームからデータを抽出し、concatを使って連結させる場合に注…
今回はSciPyを使ってSavitzky-Golay法によるデータの平滑化、一次微分、二次微分の方法を紹介します。
Savitzky-Golay法はデータのある区間を多項式で近似します。
近似式とすることでデータの平滑化ができ、また微分も可能にします。
また多項式で近似するデータの区間は少しずつ移動していくことから移動平均の一種（重み付き移動平均）として、ノイズが多いデータの解析に広く使われています。
今回はそのSavitzky-Golay法をPythonのSciPyでやってみようというお話です。
まずはノイズ付きの信号データをガウス関数を使って作ってみました。
import numpy as np
import matplotlib.pyplot as plt
import random
x_min = 0
x_max = 100
noise_level = 0.02
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.show()
実行結果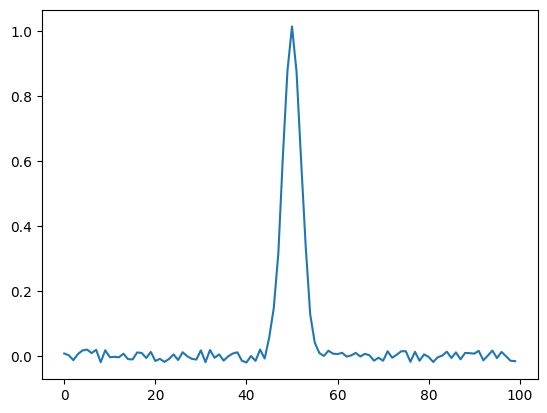
このプログラムでは「x_min」と「x_max」の中間にピークをもつデータを作成します。
またその際、「noise_level」で指定した比率でランダムノイズが追加されます。
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_listパラメータを指定しているのはこちらです。
parameter = [1, (x_min+x_max)/2, 2]それでは始めていきましょう。
Savitzky-Golay法によるデータの平滑化
まずはSavitzky-Golay法によるデータの平滑化を試してみます。
「SciPyのsignal」をインポートし、「signal.savgol_filter(Y値のリスト, 多項式を計算する点の数, 多項式の次数, deriv=0)」とします。
まずは多項式の次数２、多項式を計算するデータ数５として試してみます。
import numpy as np
import matplotlib.pyplot as plt
import random
#----------この部分を追加----------
from scipy import signal
#----------この部分を追加----------
x_min = 0
x_max = 100
noise_level = 0.02
#----------この部分を追加----------
degree = 2
window = 5
#----------この部分を追加----------
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
#----------この部分を追加----------
yma_list = signal.savgol_filter(y_list, window, degree, deriv=0)
#----------この部分を追加----------
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
#----------この部分を追加----------
plt.plot(x_list, yma_list)
#----------この部分を追加----------
plt.show()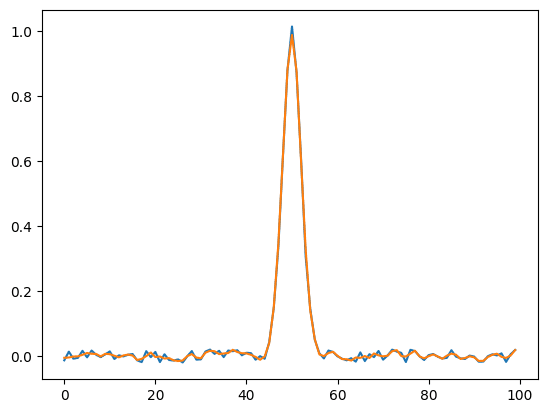
多項式を計算するデータ数を増やすと、データが平滑化されますが、やりすぎると元の形から大きく変わってしまいます。
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy import signal
x_min = 0
x_max = 100
noise_level = 0.02
degree = 2
#----------この部分を変更----------
window = 25
#----------この部分を変更----------
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
yma_list = signal.savgol_filter(y_list, window, degree, deriv=0)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
実行結果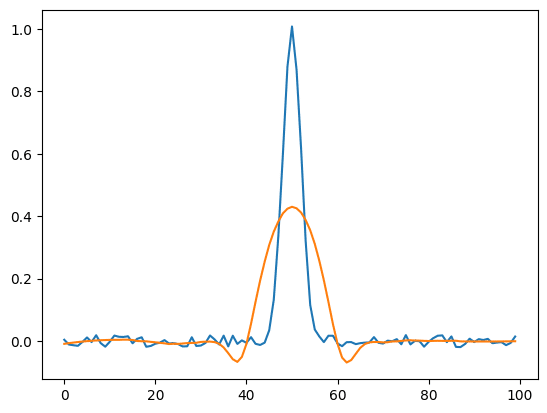
多項式の次数を大きくすると元のデータにより合いやすくなり、平滑化されなくなります。
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy import signal
x_min = 0
x_max = 100
noise_level = 0.02
#----------この部分を変更----------
degree = 4
#----------この部分を変更----------
window = 5
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
yma_list = signal.savgol_filter(y_list, window, degree, deriv=0)
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
Savitzky-Golay法によるデータの微分
次にSavitzky-Golay法によるデータの微分を試してみましょう。
データの微分をするには先ほどの「signal.savgol_filter(Y値のリスト, 多項式を計算する点の数, 多項式の次数, deriv=0)」の「deriv=0」の数値を微分したい回数に変えます。
つまり「deriv=1」なら１次微分、「deriv=2」なら２次微分というわけです。
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy import signal
x_min = 0
x_max = 100
noise_level = 0.02
degree = 2
window = 5
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
#----------この部分を変更----------
yma_list = signal.savgol_filter(y_list, window, degree, deriv=1)
#----------この部分を変更----------
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
実行結果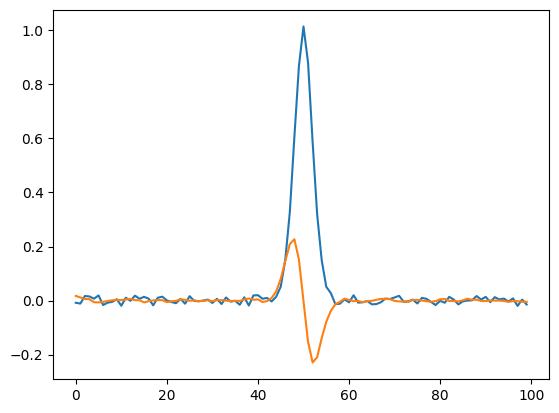
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy import signal
x_min = 0
x_max = 100
noise_level = 0.02
degree = 2
window = 5
def gauss_noise(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) + random.uniform(-noise_level, noise_level) for x in x_list]
return y_list
x_list = np.arange(x_min, x_max, 1)
parameter = [1, (x_min+x_max)/2, 2]
y_list = gauss_noise(x_list, parameter[0], parameter[1], parameter[2])
#----------この部分を変更----------
yma_list = signal.savgol_filter(y_list, window, degree, deriv=2)
#----------この部分を変更----------
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_list)
plt.plot(x_list, yma_list)
plt.show()
実行結果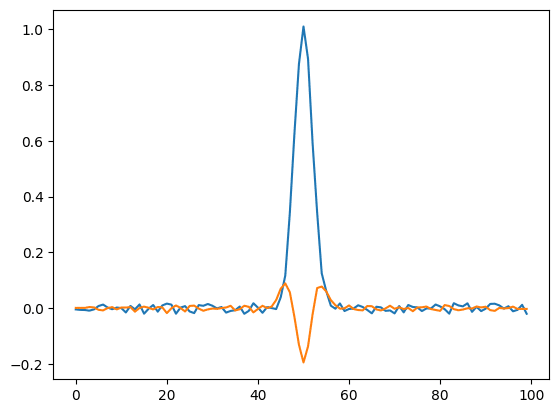
次回はSciPyを使ってガウス分布（正規分布）のグラフを描く方法を紹介します。
ではでは今回はこんな感じで。
あわせて読みたい
コメント