SciPy
前回、PythonのSciPyを使ってSavitzky-Golay法によるデータの平滑化、一次微分、二次微分の方法を紹介しました。
今回はSciPyを使ってガウス分布(正規分布)のグラフを描く方法を紹介します。
ガウス分布に関してはこれまで自作関数を使ってきました。

def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_listただどうやら調べていくとSciPyの中にガウス分布のグラフを作成できる関数があるようでしたので、今回試してみました。
それでは始めていきましょう。
SciPyでガウス分布のグラフを作成
SciPyでガウス分布のグラフを作成するにはまず「scipy.stats」の「norm」をインポートします。
from scipy.stats import normそして「norm.pdf(Xのリスト)」とします。
ちなみにpdfは確率密度関数(Probability Density Function)の頭文字です。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y = norm.pdf(x)
fig = plt.figure()
plt.clf()
plt.plot(x, y)
plt.show()
実行結果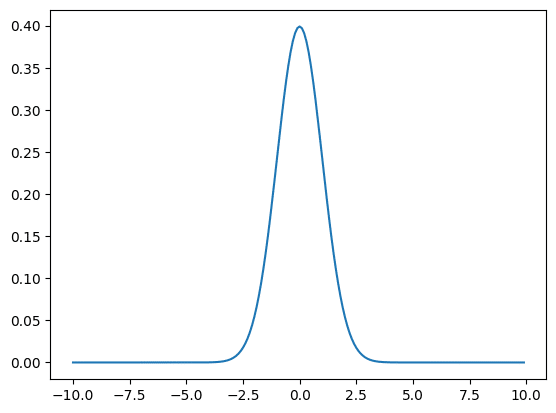
またオプション引数として「loc」と「scale」を追加することも可能で、「loc」はピーク位置、「scale」はピークの広がりを制御する値です。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y = norm.pdf(x, 5)
fig = plt.figure()
plt.clf()
plt.plot(x, y)
plt.show()
実行結果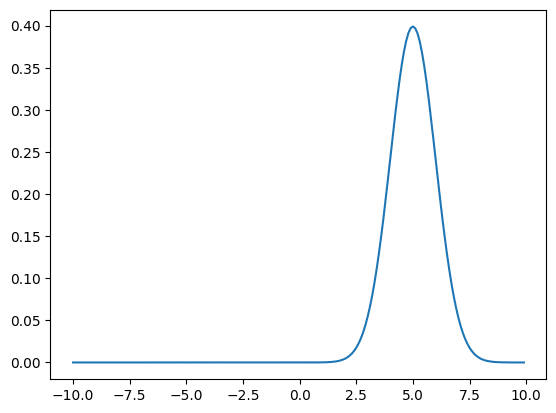
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y = norm.pdf(x, 0, 3)
fig = plt.figure()
plt.clf()
plt.plot(x, y)
plt.show()
実行結果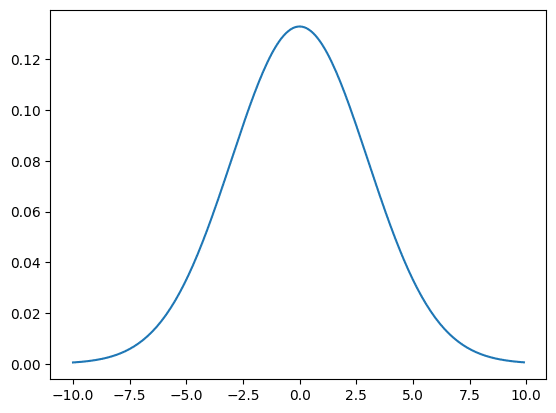
ちなみに「loc」も「scale」もリストを引数にすることもでき、複数のガウス分布が混ざったグラフを描くこともできるようです。
とりあえず使ってみましたが、値とグラフの関係性はまだよく理解できていません。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
import random
x = np.arange(-10, 10, 0.2)
y = norm.pdf(x, np.random.uniform(0,10,len(x)), np.random.uniform(0, 5, len(x)))
fig = plt.figure()
plt.clf()
plt.plot(x, y)
plt.show()
実行結果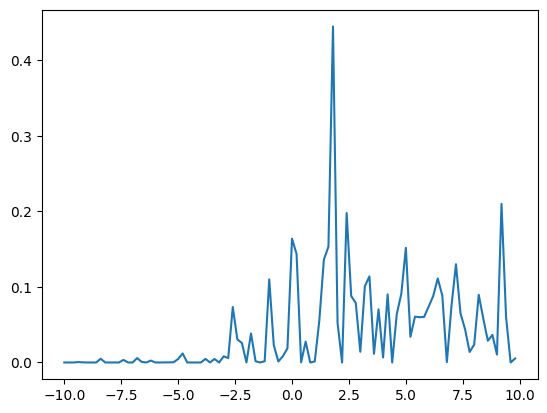
最大値を固定する方法
前に使用していた自作関数では「a」の値を変えることでピークの最大値を変えることができていました。
def gauss(x_list, a=1, m=0, s=1):
y_list = [a * np.exp(-(x - m)**2 / (2*s**2)) for x in x_list]
return y_listしかし今回の関数の実行結果を見てみると、「scale」を変えるとピークの高さが変わってしまうようです。
そこでピークの値を「1」にできるよう少し工夫してみました。
やり方としては値全体をピークの最大値で割るだけです。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y_temp = np.array(norm.pdf(x, 0, 3))
y = y_temp/np.max(y_temp)
fig = plt.figure()
plt.clf()
plt.plot(x, y)
plt.show()
実行結果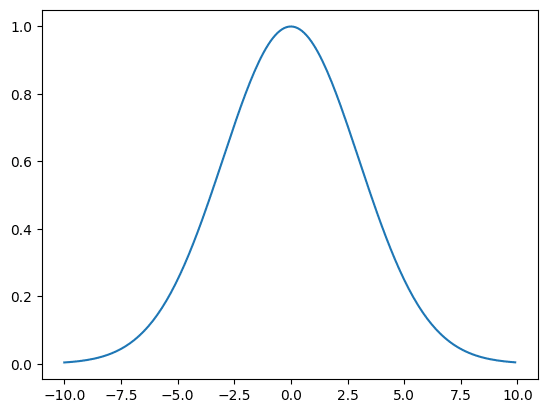
累積分布関数
先ほどまでのグラフは確率密度関数といい、そのある範囲でその事象が起こる確率を示したグラフになります。
そしてこのような確率を表すグラフとしてもう一つ重要なのが「累積分布関数」です。
これはグラフの左側から右側に行くに従って、確率を足し合わせて行ったもので、特定の事象までにおいてどれくらいの確率で起こるかを示すものです。
この累積分布関数を表示するには「norm.pdf()」の代わりに「norm.cdf()」を用います。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y1 = norm.cdf(x)
y2 = norm.cdf(x, 5)
y3 = norm.cdf(x, 0, 3)
fig = plt.figure()
plt.clf()
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.show()
実行結果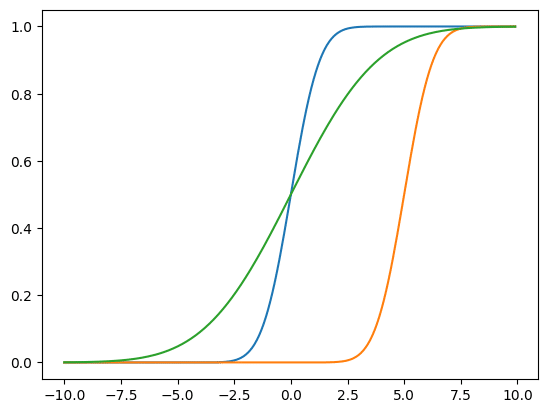
今回は「scipy.stats」を使ったガウス分布(正規分布)のグラフの描き方を紹介しましたが、「scipy.stats」では他の分布も用意されています。
ということで次回は「scipy.stats」を使った色々な分布の描き方を紹介します。
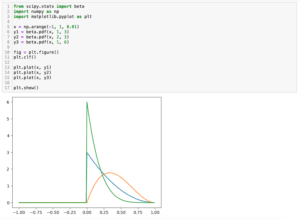
ではでは今回はこんな感じで。

コメント