matplotlib
前回、PythonのScikit-learnで二つのグラフの一致度を確認する方法を紹介しました。
今回はガウス分布、ラプラス分布、ローレンツ分布を自作関数化してグラフ表示する方法を紹介します。
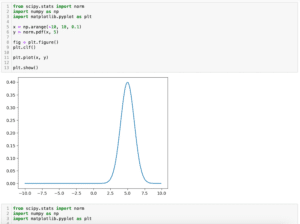
ちなみにガウス分布に関してはこちらの記事でも紹介していますので、よかったらどうぞ。

ちなみに今回は数式上、ピーク高さが一致する様に作成しています。
それでは始めていきましょう。
(私は数学の素人なので数学的に間違っている場合もありますので、ご注意ください)
ガウス分布
まずはガウス分布です。
\(f(x) = a \times exp \{ – \frac{(x – \mu)^2}{2\sigma^2}\}\)
aがピーク高さ、\(\mu\)がピーク位置、\(\sigma\)がピークの広がりを示します。
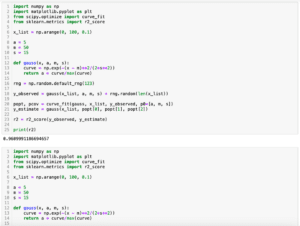
import numpy as np
import matplotlib.pyplot as plt
x_list = np.arange(0, 100)
def gauss(x, a, m, s):
curve = np.exp(-(x - m)**2/(2*s**2))
return a * curve/max(curve)
gauss_param = [5, 50, 10]
y_gauss = gauss(x_list, gauss_param[0], gauss_param[1], gauss_param[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_gauss)
plt.show()
実行結果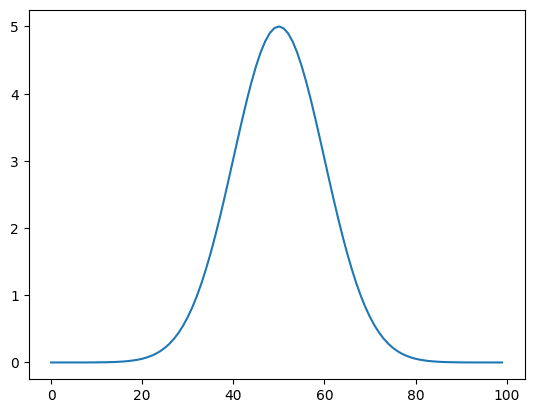
ラプラス分布
ラプラス分布は次の式で得られる分布です。
\(f(x) = \frac{1}{2b} \times exp \{ – \frac{|x – \mu|}{b}\}\)
aがピーク高さ、\(\mu\)がピーク位置、bがピークの広がりを示します。
import numpy as np
import matplotlib.pyplot as plt
x_list = np.arange(0, 100)
def laplace(x, a, m, b):
curve = 0.5 * b * np.exp(-1 * abs(x - m)/b)
return a * curve/max(curve)
laplace_param = [5, 50, 10]
y_laplace = laplace(x_list, laplace_param[0], laplace_param[1], laplace_param[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_laplace)
plt.show()
実行結果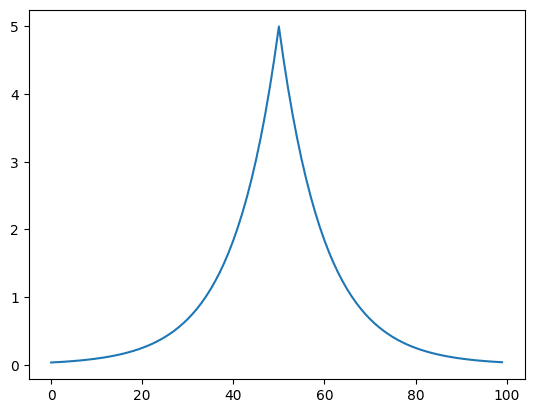
ローレンツ分布(コーシー分布)
ローレンツ分布は下の式で得られる分布です。
\(f(x) = \frac{1}{\pi} \times \frac{\gamma}{(x – x0)^2 + \gamma ^2}\)
aがピーク高さ、\(x0\)がピーク位置、\(\gamma\)がピークの形状を示します。
import numpy as np
import matplotlib.pyplot as plt
x_list = np.arange(0, 100)
def lorentz(x, a, x0, g):
curve = (1/np.pi)*(g/((x-x0)**2 + g**2))
return a * curve/max(curve)
lorentz_param = [5, 50, 10]
y_lorentz = lorentz(x_list, lorentz_param[0], lorentz_param[1], lorentz_param[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_lorentz)
plt.show()
実行結果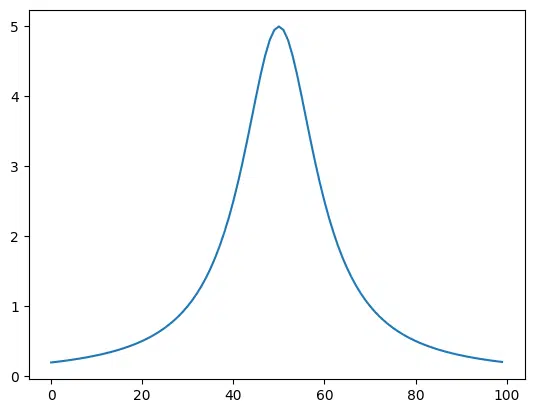
三つのグラフを重ねてみる
ガウス分布、ラプラス分布、ローレンツ分布はバイオや光学関係のピークフィッティングでよく出てくる(らしい)分布なので、今回勉強してみました。
自作関数があればグラフを描くだけでなく、SciPyのcurve_fitを使ってピークフィッティングをすることも可能ですの。
最後に今回出てきた3つのグラフを重ねてそれぞれの特徴を見てみましょう。
import numpy as np
import matplotlib.pyplot as plt
x_list = np.arange(0, 100)
def gauss(x, a, m, s):
curve = np.exp(-(x - m)**2/(2*s**2))
return a * curve/max(curve)
def laplace(x, a, m, b):
curve = 0.5 * b * np.exp(-1 * abs(x - m)/b)
return a * curve/max(curve)
def lorentz(x, a, x0, g):
curve = (1/np.pi)*(g/((x-x0)**2 + g**2))
return a * curve/max(curve)
gauss_param = [5, 50, 10]
y_gauss = gauss(x_list, gauss_param[0], gauss_param[1], gauss_param[2])
laplace_param = [5, 50, 10]
y_laplace = laplace(x_list, laplace_param[0], laplace_param[1], laplace_param[2])
lorentz_param = [5, 50, 10]
y_lorentz = lorentz(x_list, lorentz_param[0], lorentz_param[1], lorentz_param[2])
fig = plt.figure()
plt.clf()
plt.plot(x_list, y_gauss, label="Gauss")
plt.plot(x_list, y_laplace, label="Laplace")
plt.plot(x_list, y_lorentz, label="Lorentz")
plt.legend()
plt.show()
実行結果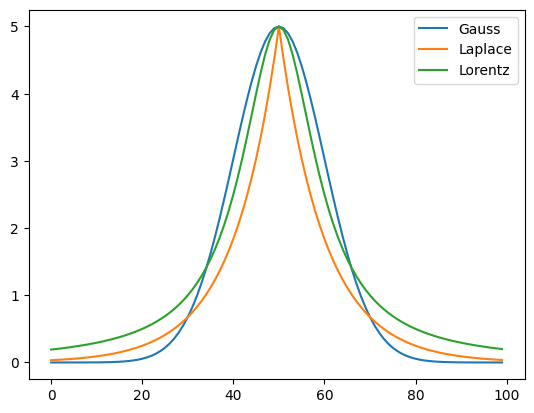
ちなみに分布に関して勉強したい方はこちらのページに色々と紹介されていますので、よかったらどうぞ。

次回はピークを境に左右の形状が非対称な分布の作成方法を紹介します。
ではでは今回はこんな感じで。

コメント