加算パイプはパイプを作るだけじゃない
前に加算パイプを使って、パイプ形状の作り方を解説しました。
この加算パイプ、実はパイプ形状を作る以外にも使い方があることを発見してしまいました。
もしかしたらみんな知っているかもしれない、もしかしたら邪道かもしれない、そんな思いを押し殺して、今回その使い方を解説していきます。
その使い方とは、円錐や三角錐(正四面体を含みます)を作ることです!
FreeCADは2次元でスケッチを作成し、それを3次元に押し出したり、削ったりすることで3次元構造を作っていきます。
つまり2次元で表しきれない3次元の構造を最初から作り出すのは難しいのです。
その最初から3次元構造を考えなければいけない形状というのが、円錐や三角錐のような錐体構造になるわけです。
今回、円錐と正四面体に関して解説していきますが、同じ方法で様々な錐体形状を作成できるようになり、デザインの幅が広がることでしょう。
ということで試していきましょう。
円錐を作ってみよう
まずは簡単な方である円錐を作ってみましょう。
いつも通りFreeCADを起動したら、新規作成、XY平面にスケッチを作成します。


適当に円を描き、

円の半径を 25 mmに拘束し、

円の中心の位置を原点と点拘束します。


これで一旦スケッチを抜け、再度XY平面にスケッチを作成します。

適当に円を描き、

円の中心を原点と点拘束します(今回はこちらを先にやってください)。

そして円の半径を3Dプリンタではプリントできないほど小さい値にします。
今回 0.001 mm (1 μm)にしました。
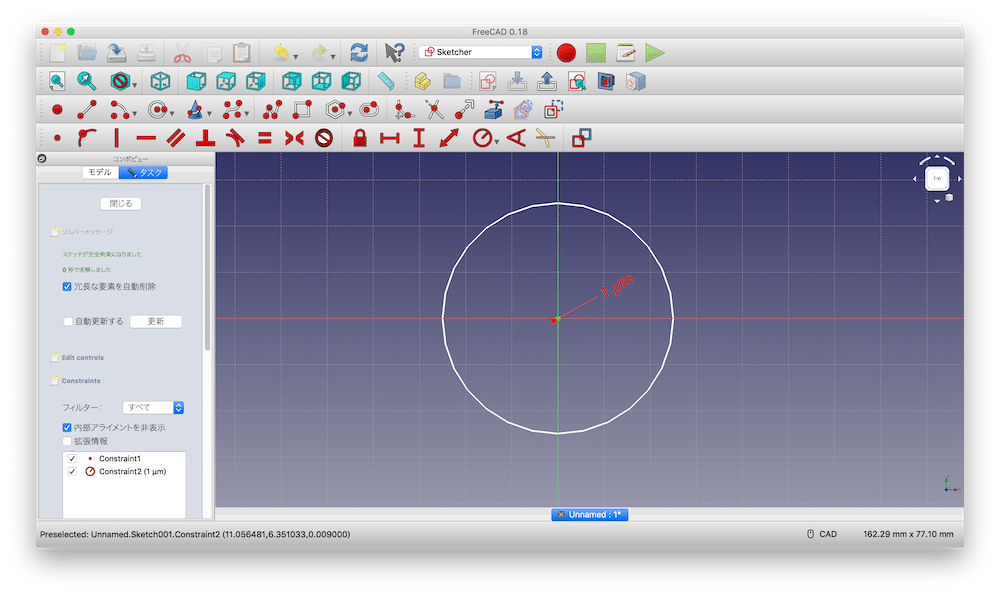
スケッチを抜け、今度はXZ平面にスケッチを作成します。

Z軸に平行になるよう線を描き、

下の点を原点と点拘束し、

線の長さを50 mmに拘束します。

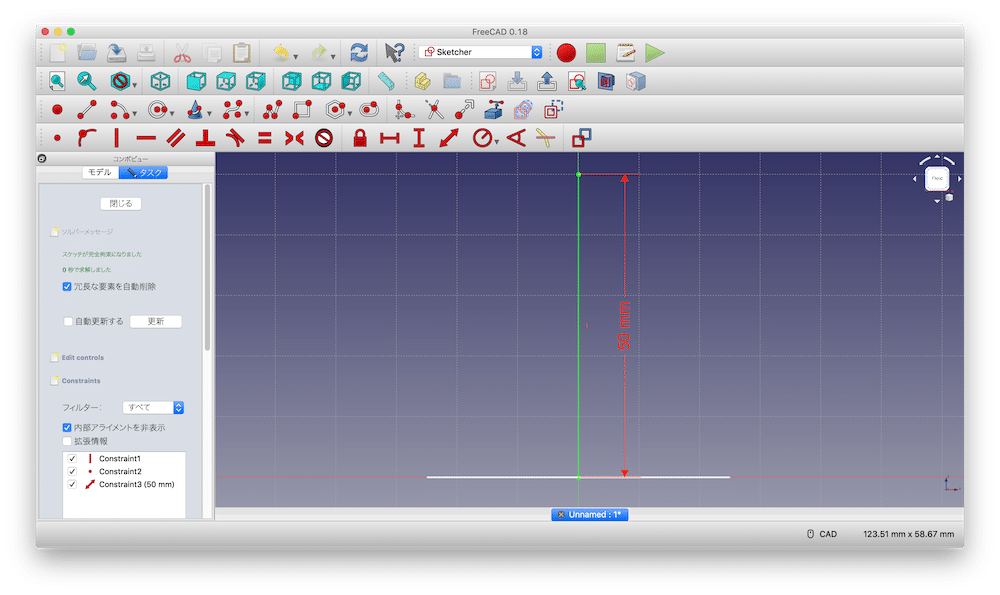
これでスケッチは完了です。
今度は頂点となる極小の円を移動していきます。
極小の円をクリックするか、左側のウインドウで「Sketch001」をクリックします。
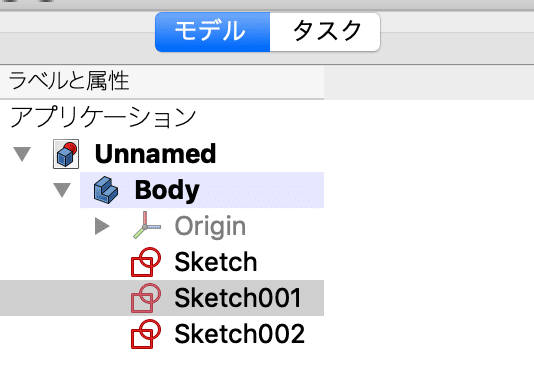
左下のウインドウで、Attachment > Position > z の値を50 mmにします。
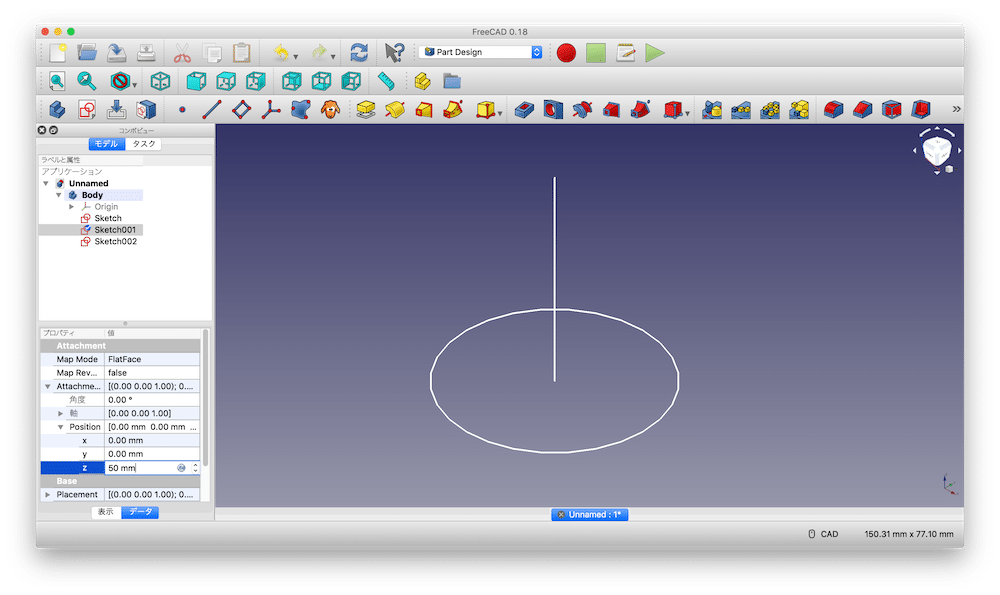
斜めから見るとこんな感じです。
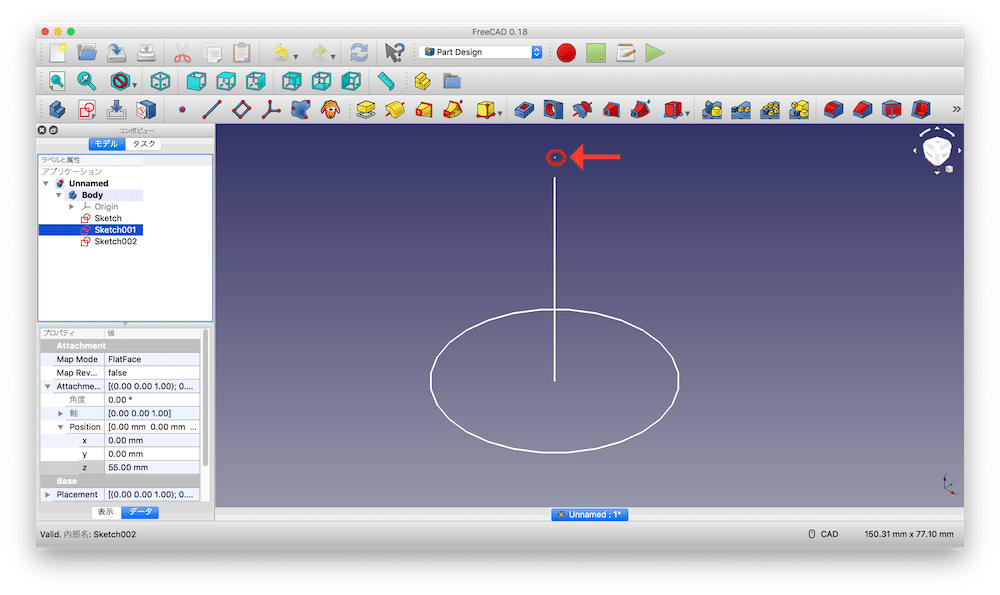
極小の円が移動できたか分からない場合は、さらに数 mm移動させて、位置が変わるか確認してみましょう。
移動できたら、左側のウインドウの「Sketch001」をクリックして、加算パイプをクリックします。

オブジェクトをクリックして、経路となる線(Sketch002)をクリック。
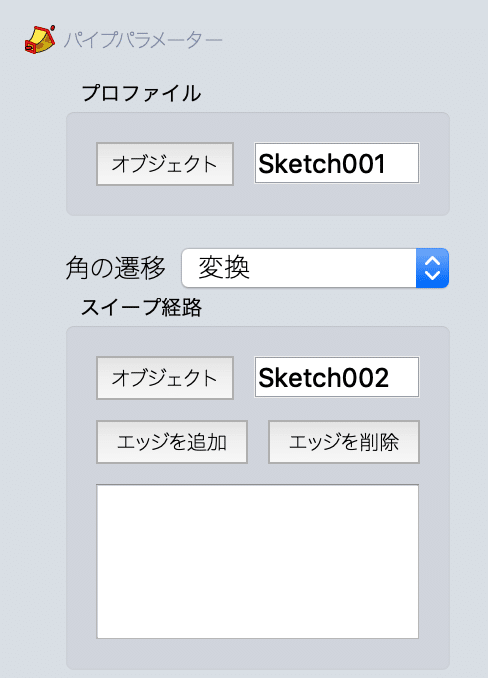
そして左のウインドウの下の方へ行き、断面変換の変換モードを「マルチ断面」にします。
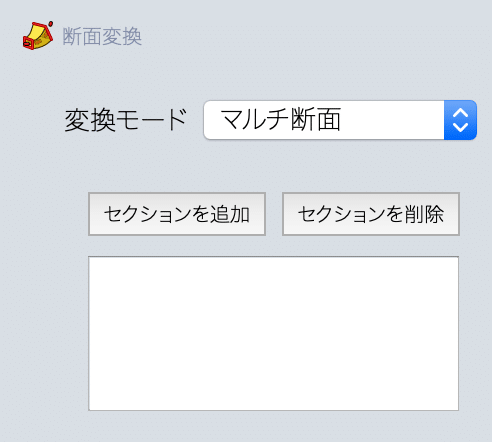
そして「セクションを追加」をクリックして、大きい円をクリックしてください。
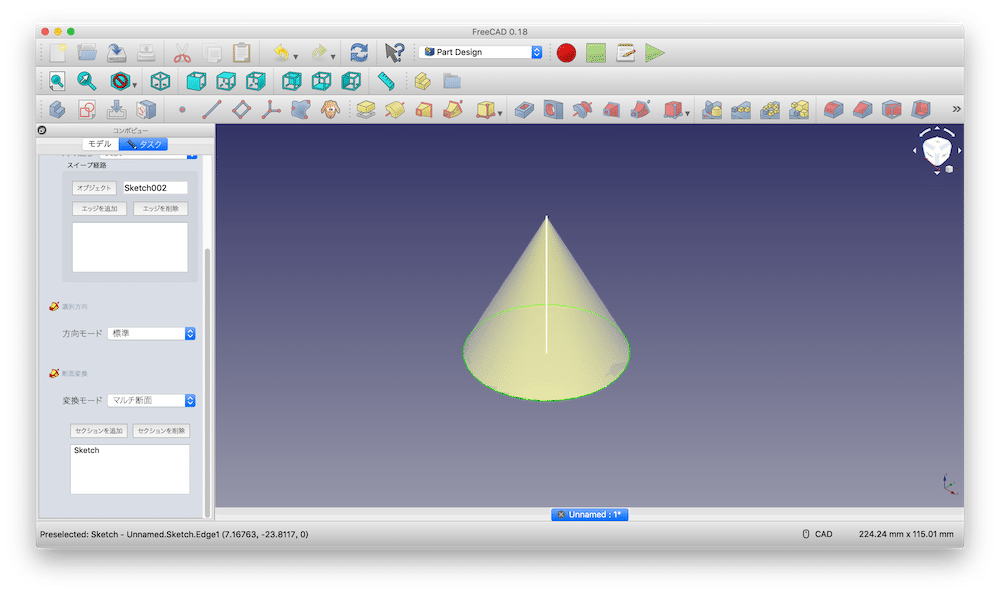
思った通り、円錐ができそうですね。
これで「OK」をクリックして、加算パイプを抜ければ、出来上がりです。
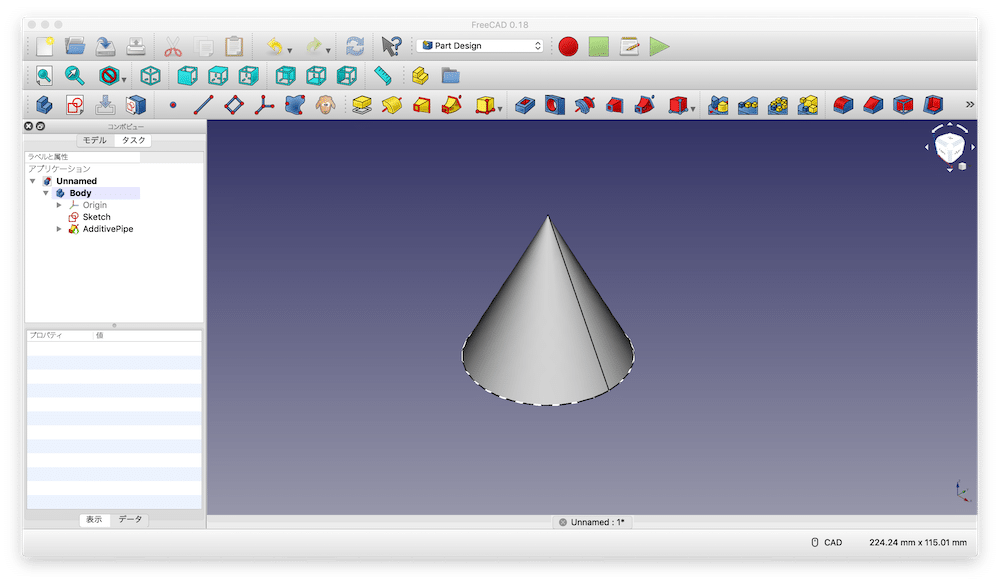
もちろん頂点の極小の円をサイズを変えることにより、円錐台と呼ばれる頂点も平面の形を作ることもできます。
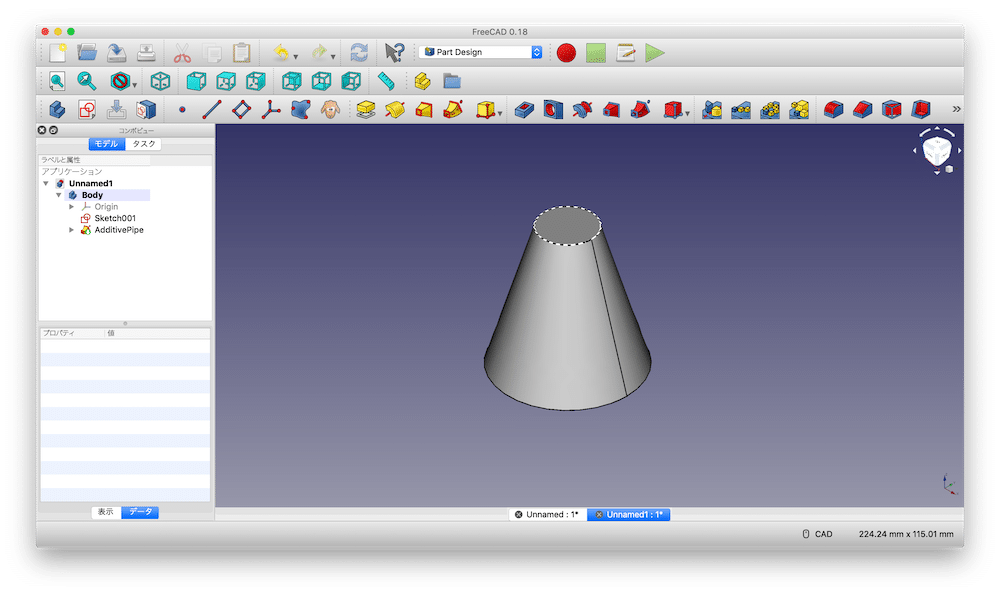
正四面体を作ってみる
次に同じように加算パイプを使って、正四面体を作っていきます。
しかし円錐と比べると、正四面体は少し厄介です。
実は正四面体を作るためには、重心という概念を学ばねばなりません。
重心というのは、三角形を一点で支えた時にバランスが取れる場所のことを言います。
そして正四面体の頂点は底面の正三角形の重心の上にあるのです。
まずはこの重心の計算方法を学んでいきましょう。
重心の計算方法
重心はそれぞれの頂点から逆側にある辺に垂直な線を引き、3本の線が交わったところになります。
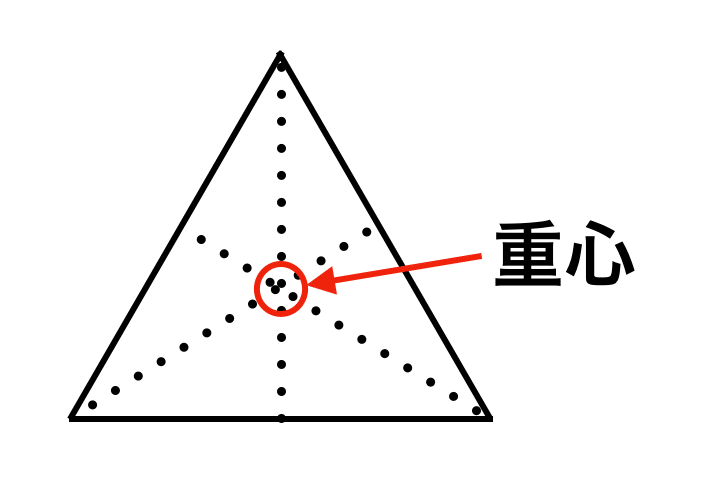
重心の座標の計算方法は、それぞれの頂点のX座標、Y座標を足し、3で割った数です。
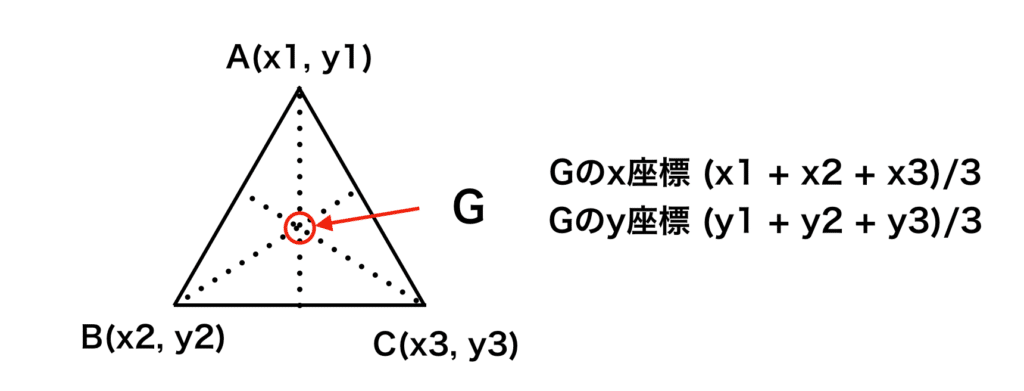
今回はBの座標を(0 , 0)とし、Cの座標を(20, 0)とします。
するとAのX座標はBとCのX座標の真ん中なので 10 となります。
ではAのY座標はいくつでしょうか?
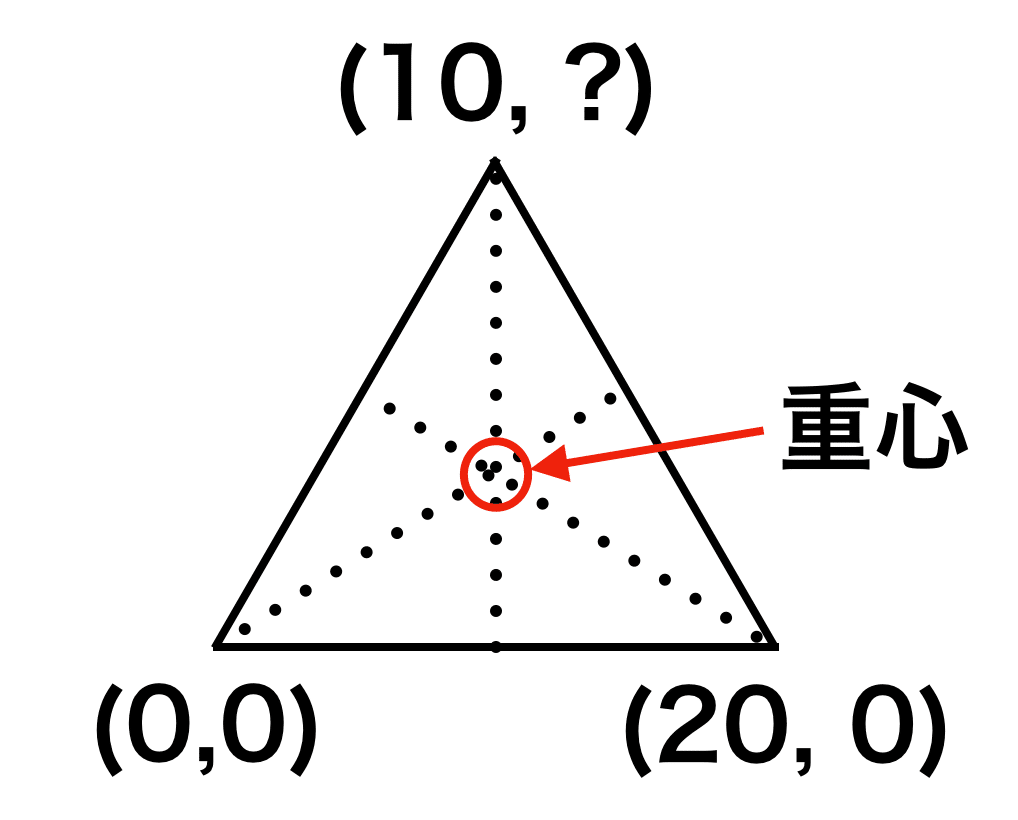
これは三角関数を用いて、算出することができます。
正三角形を縦に真っ二つに割ると、30°、60°、90°の直角三角形となります。
この辺の長さの比はそれぞれ1:2 : √3となります。
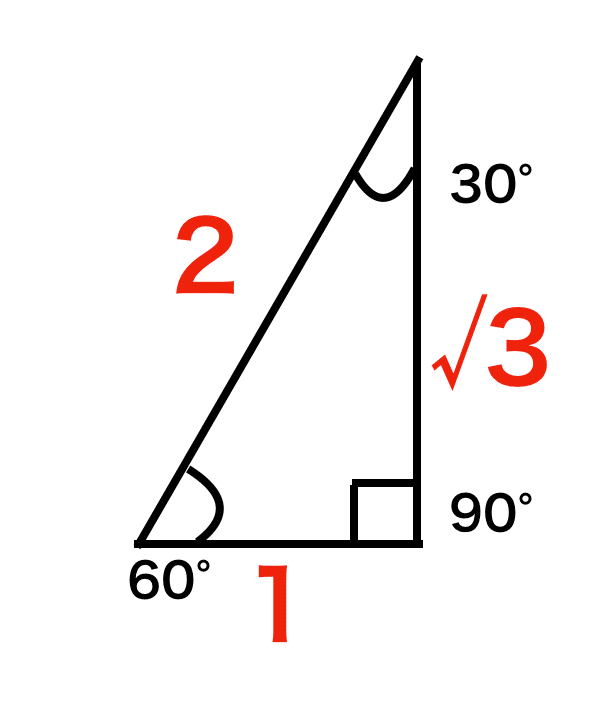
これにより以下の式から、AのY座標を計算することができます。
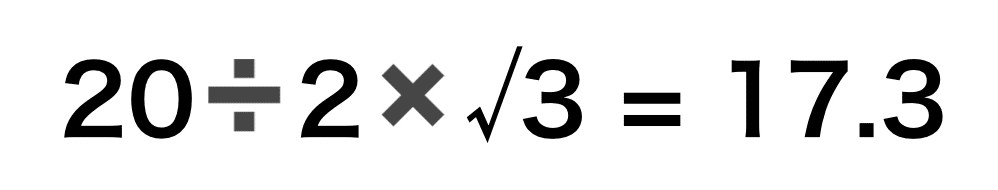
実際は小数点以下は永遠と続くのですが、数字を丸めて17.3としています。
頂点の高さも同じ計算で得られ、今回の三角錐の高さは17.3 mmとなりますので、覚えておいてください。
これで3点の座標を得ることができました。
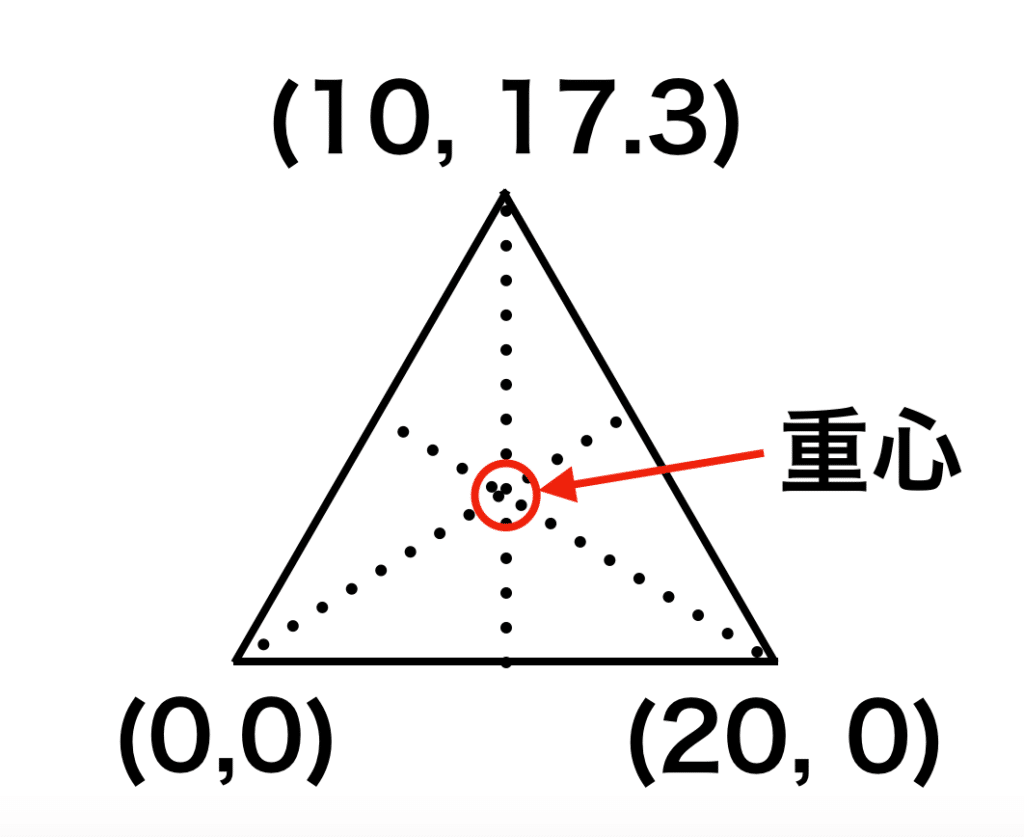
この3点の座標を使って重心を計算していきましょう。
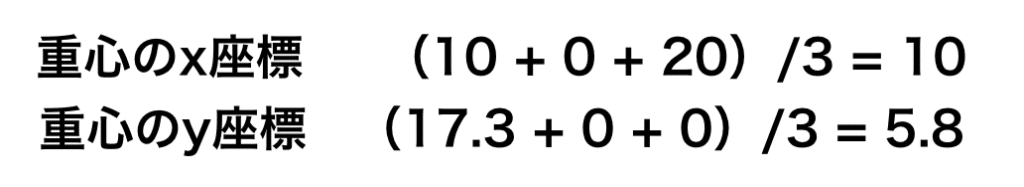
ちなみに数字は丸めています。
ということで重心は(10 , 5.8)ということが分かりました。
これを頭にいれ、正四面体をデザインしていきましょう。
正四面体を作ってみよう
いつも通りFreeCADを起動し、新規作成、XY平面にスケッチを作成します。


線を使って、適当に三角形を描きます。

左下の点を原点に点拘束し、

各辺の長さを20 mmに拘束します。

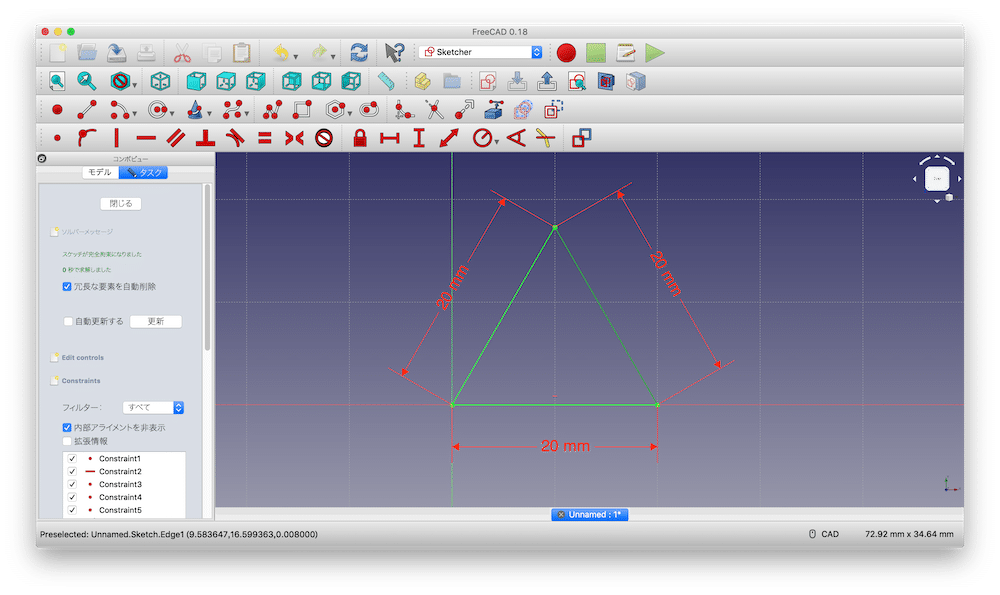
これで底面は完成です。
スケッチを抜け、新たにXY平面にスケッチを作成します。

そして線を使って、適当に三角形を描きます。
この時、どの線も軸に平行にならないように注意してください。

そして左下の点の位置をX:9.99 mm、Y:5.79 mmに、
右下の点の位置をX:10.01 mm、Y:5.79 mmに、
頂点の位置をX:10 mm、Y:5.81 mmに拘束します。

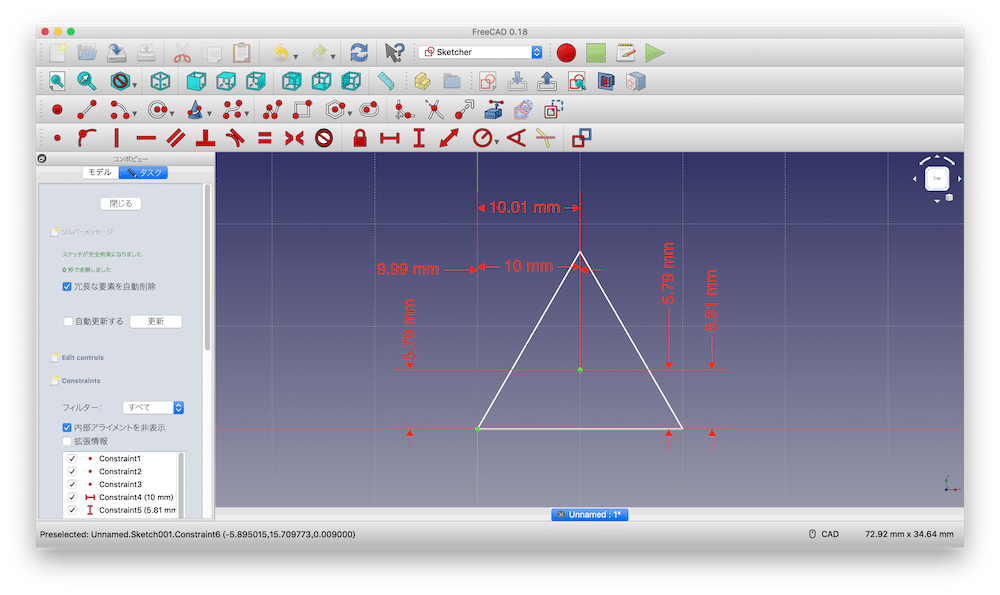
これで頂点のデザインは完了ですので、スケッチを抜けます。
次にXZ平面にスケッチを作成し、

Z軸に平行になるように線を描きます。

線の下側の線の位置をX:10 mm、Z:0 mmに拘束し、

線の長さを 17.3 mmに拘束します。

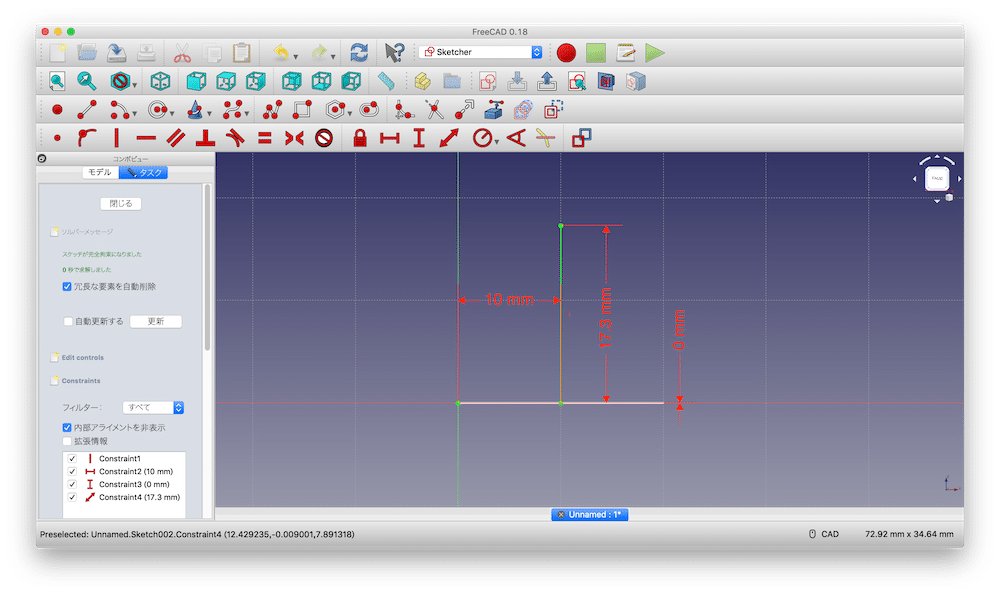
これでスケッチは完了ですので、スケッチを抜けます。
先ほどの極小の三角形の位置をずらしていきます。
左のウインドウで「Sketch001」をクリックするか、デザインエリアの極小の三角形をクリックして、選択します。
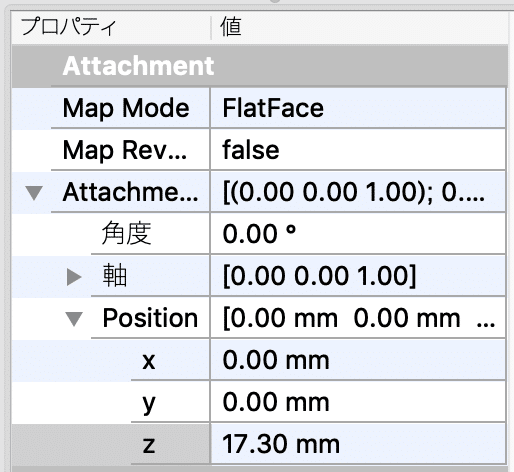
左下のウインドウの Attachment > Position > z の値を 17.3 mmにします。
するとデザインはこん感じになるかと思います。
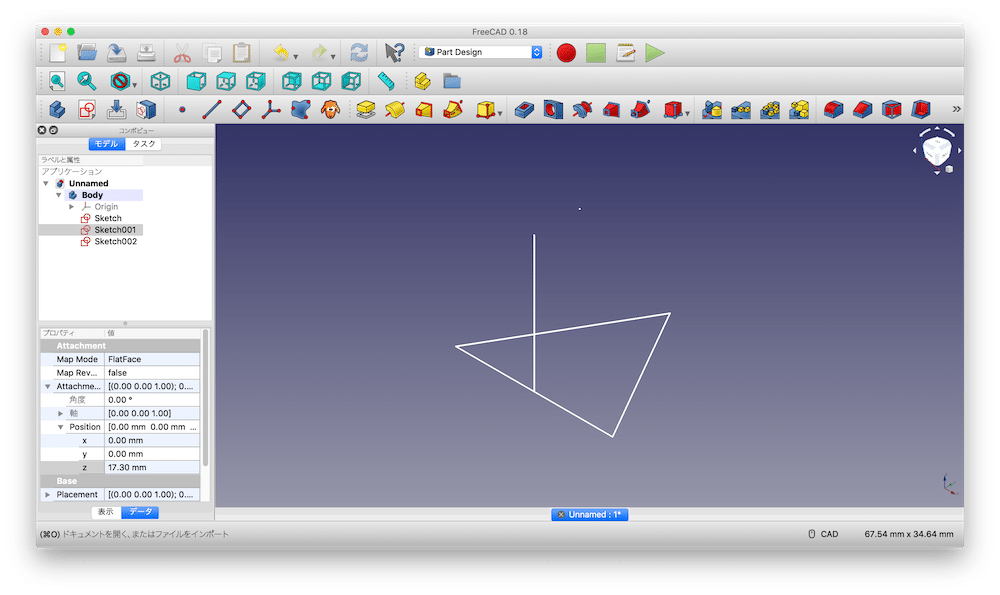
加算パイプを用いて、正四面体を作っていきます。
まずは極小の点をクリックするか、左のウインドウで「Sketck001」をクリックして、選択します。
そして加算パイプをクリックします。

オブジェクトをクリックして、線(Sketch002)をクリックします。
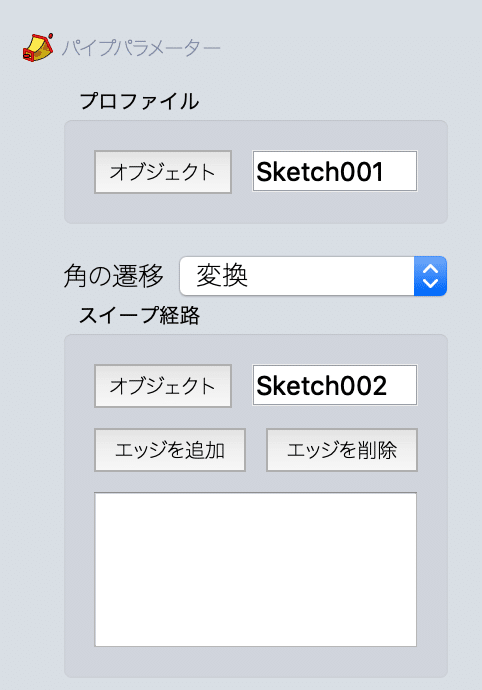
さらに左のウインドウの下側に行き、断面変換の変換モードをを「マルチ断面」にします。
「セクションを追加」をクリックし、大きな三角形(Sketch)をクリックします。
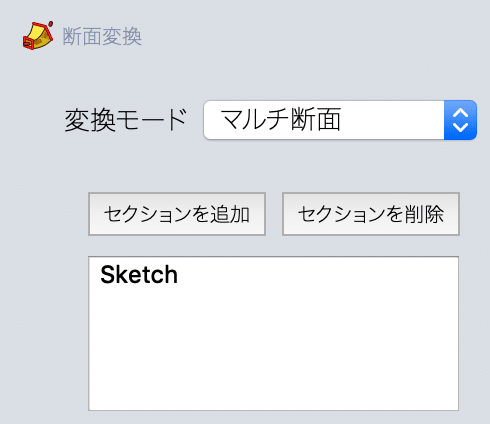
正四面体が現れました。
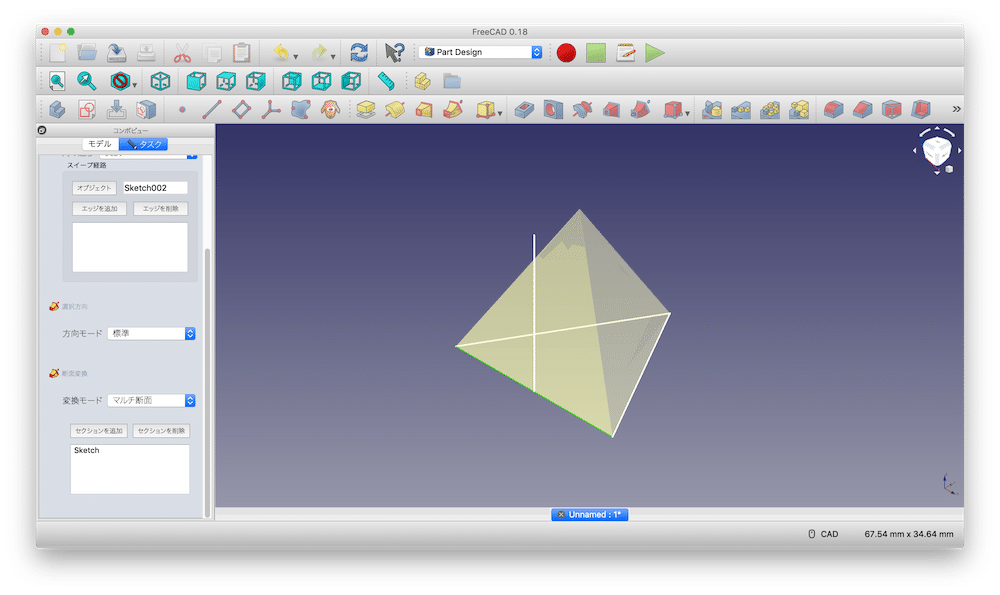
これで左のウインドウの「OK」をクリックすると、加算パイプが終了します。
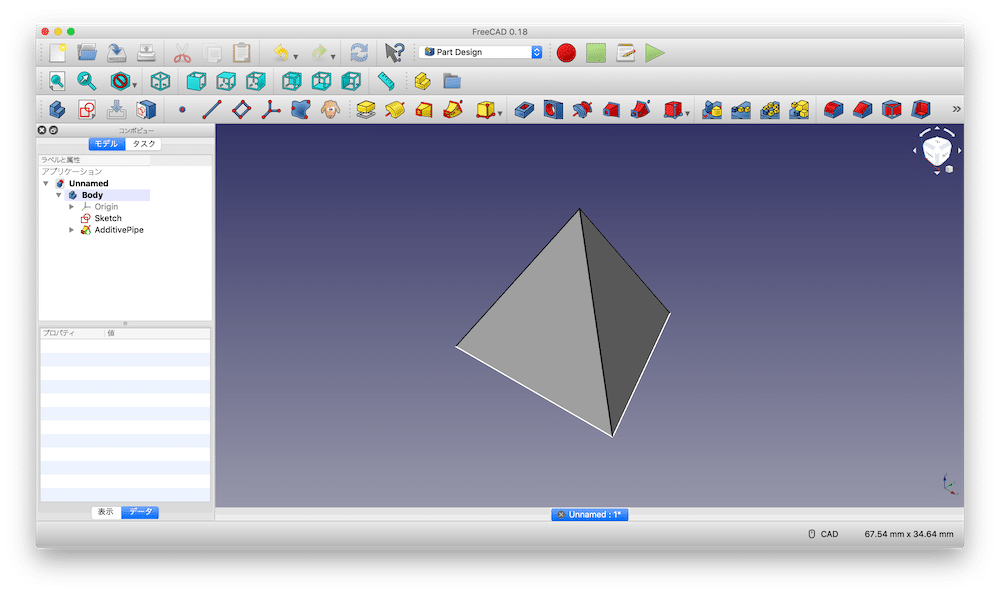
正四面体が完成しました。
円錐の時と同様、三角錐の場合も頂点の極小の三角形のサイズを変えることで、三角錐台を作ることも可能です。
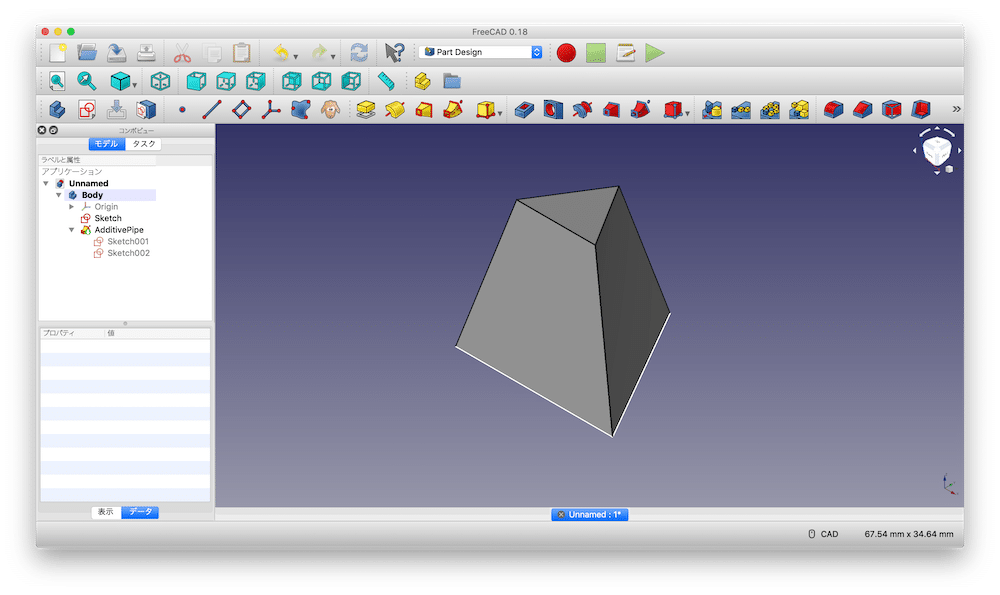
ぜひぜひ色々と試してみてください。
次回はUltimaker Curaでインフィルの密度を変えるとどんな感じになるのか検証してみたいと思います。

とりあえず今回はこんな感じで。

コメント