機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnのボストンの住宅価格を予想するのにLassoモデルとElasticNetモデルを使ってみました。
ただ結果としては残念なことに、線形回帰(LinearRegression)と比べて、どちらのモデルも予想の精度が改善するということはありませんでした。
もちろんこれだけでLassoモデルやElasticNetモデルがダメなモデルというわけではありません。
それぞれのモデルに複雑なオプションがあるので、調整していくと精度が改善することは十分に考えられます。
でもまずは回帰を行うために、どんなモデルがあるのかというのをみて、大まかに傾向をつかんでいきたいと思います。
ということで今回は残りの2つのRidgeRegressionモデルとSVRモデルを試してみましょう。
SVRモデルは機械学習モデルマップでは「SVR(kind=”linear”)」と「SVR(kind=”rbf”)」があるので、こちらも両方とも試していきます。
ということでまずは準備から。
前回同様、まずはデータセットを読み込みます。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
from sklearn.model_selection import train_test_split
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果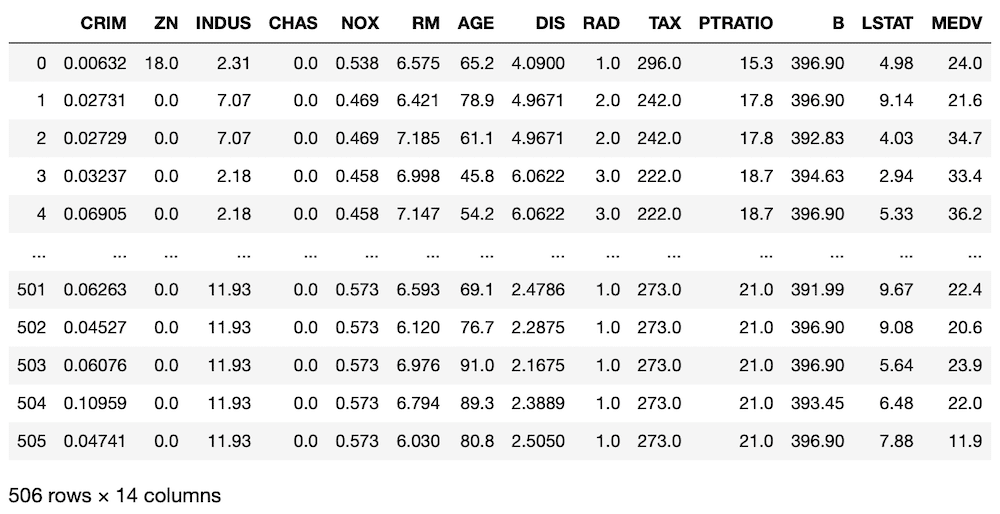
次にこちらも前回同様、学習・評価を繰り返し行うためのプログラムを書いていきます。
使うデータは「犯罪率(CRIM)」、「平均部屋数(RM)」、「低所得者の割合(LSTAT)」の3つ。
データセットを分割したのち、同じ訓練用データを使って、異なる機械学習モデルで学習させ、その結果を表示させます。
それをfor文を使って、100回繰り返します。
比較対象となる機械学習モデルとして「線形回帰(LinearRegression)」のプログラムはこんな感じです。
<セル2>
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np
trial = 100
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
pred_lr_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_lr = LinearRegression()
model_lr.fit(x_train, y_train)
pred_lr = model_lr.predict(x_test)
pred_lr_score.append(r2_score(y_test, pred_lr))
pred_lr_ave = np.average(np.array(pred_lr_score))
print(pred_lr_ave)
実行結果
0.6314731664384512ここにRidgeRegressionモデルやSVRモデルの機械学習を組み込んでいきましょう。
SVR(Support Vector Regression)
前回、RedgeRegressionモデルは線形回帰(LinearRegression)に基づいていて、その変形版であるということを解説しました。
ではSVRとはどう言ったモデルなのでしょうか?
SVRはSupport Vector Regressionというモデルで、この名前を聞いたときに「あれ?」と思う方もいることでしょう。
前にSVM(Support Vector Machine:サポートベクターマシン)を使って、iris(アヤメ)の種類を予測する機械学習を試しました。
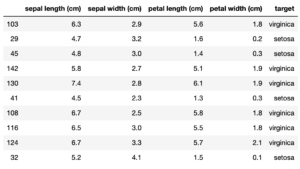
ただSVMの場合は、特徴量の散布図中に線を引いて、どっち側にあるかという結果から、分類を予想するというものでした。
実はSVRも同じ考えを使っていて、特徴量の散布図中に線を引いて、それぞれの点がどれくらいその線から離れているかという情報を使い、分類ではなく、「数値」を予想するものになります。
私はそんなに詳しく解説はできないので、こちらのサイトをご覧ください。

それでは組み込んでいきましょう。
RidgeRegressionモデル、SVRモデルを組み込む
RidgeRegressionモデル、SVRモデルを組み込むのは今までと同様、モデルをインポートして、組み込んでいきます。
RidgeRegressionとSVRを組み込むにはこんな感じでインポートします。
from sklearn.linear_model import Ridge
from sklearn.svm import SVRそしてモデルを変数に格納します。
今回、SVRモデルは”linear”と”rbf”をオプションで指定します。
model_rd = Ridge()
model_svr_lr = SVR(kernel='linear')
model_svr_rbf = SVR(kernel='rbf')そしていつものように機械学習をするということです。
model_rd.fit(x_train, y_train)
model_svr_lr.fit(x_train, y_train)
model_svr_rbf.fit(x_train, y_train)ということで先ほど線形回帰モデルを使って書いた繰り返しプログラムに入れ込んでいきましょう。
<セル2変更>
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np
trial = 100
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
pred_lr_score = []; pred_rd_score = []; pred_svr_lr_score = []; pred_svr_rbf_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_lr = LinearRegression()
model_rd = Ridge()
model_svr_lr = SVR(kernel='linear')
model_svr_rbf = SVR(kernel='rbf')
model_lr.fit(x_train, y_train)
model_rd.fit(x_train, y_train)
model_svr_lr.fit(x_train, y_train)
model_svr_rbf.fit(x_train, y_train)
pred_lr = model_lr.predict(x_test)
pred_rd = model_rd.predict(x_test)
pred_svr_lr = model_svr_lr.predict(x_test)
pred_svr_rbf = model_svr_rbf.predict(x_test)
pred_lr_score.append(r2_score(y_test, pred_lr))
pred_rd_score.append(r2_score(y_test, pred_rd))
pred_svr_lr_score.append(r2_score(y_test, pred_svr_lr))
pred_svr_rbf_score.append(r2_score(y_test, pred_svr_rbf))
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_rd_ave = np.average(np.array(pred_rd_score))
pred_svr_lr_ave = np.average(np.array(pred_svr_lr_score))
pred_svr_rbf_ave = np.average(np.array(pred_svr_rbf_score))
print(pred_lr_ave, pred_rd_ave, pred_svr_lr_ave, pred_svr_rbf_ave)
実行結果
/opt/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:193: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
(以下略)警告が出てしまいました。
FutureWarningということで、今はいいけど将来エラーになるということでしょう。
内容としては「The default value of gamma will change from “auto” to “scale” in version 0.22 to account better for unscaled feature.」ということです。
SVMにはgammaというオプションがあって、そのデフォルトが”auto”から”scale”に変わるから気をつけてねということでした。
この警告は、gammaのオプションを指定することで解消されます。
ということでこんな感じ。
<セル2変更>
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np
trial = 100
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
pred_lr_score = []; pred_rd_score = []; pred_svr_lr_score = []; pred_svr_rbf_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_lr = LinearRegression()
model_rd = Ridge()
model_svr_lr = SVR(kernel='linear')
model_svr_rbf = SVR(kernel='rbf', gamma="scale")
model_lr.fit(x_train, y_train)
model_rd.fit(x_train, y_train)
model_svr_lr.fit(x_train, y_train)
model_svr_rbf.fit(x_train, y_train)
pred_lr = model_lr.predict(x_test)
pred_rd = model_rd.predict(x_test)
pred_svr_lr = model_svr_lr.predict(x_test)
pred_svr_rbf = model_svr_rbf.predict(x_test)
pred_lr_score.append(r2_score(y_test, pred_lr))
pred_rd_score.append(r2_score(y_test, pred_rd))
pred_svr_lr_score.append(r2_score(y_test, pred_svr_lr))
pred_svr_rbf_score.append(r2_score(y_test, pred_svr_rbf))
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_rd_ave = np.average(np.array(pred_rd_score))
pred_svr_lr_ave = np.average(np.array(pred_svr_lr_score))
pred_svr_rbf_ave = np.average(np.array(pred_svr_rbf_score))
print(pred_lr_ave, pred_rd_ave, pred_svr_lr_ave, pred_svr_rbf_ave)
実行結果
0.6273969879978474 0.6275202089592343 0.6144100571192624 0.5720412974287465警告が出なくなりました。
LinearRegression、RidgeRegression、SVR(kernel=”linear”)、SVR(kernel=”rbf”)を比較してみる
プログラムもできたことですし、いつも通り5回試して、比較していきましょう。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
| LinearRegression | 0.63929 | 0.61414 | 0.61946 | 0.63439 | 0.63379 |
| RidgeRegression | 0.63932 | 0.61438 | 0.61964 | 0.63448 | 0.63391 |
| SVR(kernel=”linear”) | 0.62652 | 0.59747 | 0.60515 | 0.62396 | 0.62127 |
| SVR(kernel=”rbf”) | 0.57845 | 0.56385 | 0.57292 | 0.58113 | 0.57601 |
今回の結果としては、RidgeRegressionがLinearRegressionといい勝負をしていますが、完全に精度が上回っているというわけではなさそうです。
ということで前回、今回とボストンの住宅価格のデータセットを使って、すぐに試せそうな機械学習モデルを試してみましたが、単純にモデルを変えるだけでは精度は出ないということが分かりました。
ということはもう少し深く入っていかねばなりません。
色々調べてみると、機械学習のデータは前処理として標準化、正規化する方が予測精度が上がるということを見つけました。
ということで次回は標準化、正規化に関して、色々試していきたいと思います。
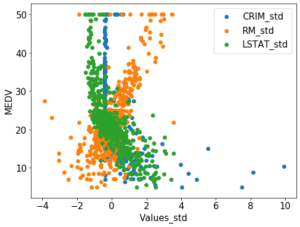
ではでは今回はこんな感じで。

コメント