機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnのボストンの住宅価格を予想するのにデータを標準化、正規化をした後、RidgeモデルとSVRモデルで機械学習をしてみました。
その結果、SVRモデルを標準化、正規化することで予測結果のスコアが良くなることがわかりました。
ただここで考えるべきことは、見かけ上スコアが良くなったのか、それとも本当に予測精度が上がったのかです。
今回は正解値と予測値をグラフにプロットしてみることで、どれくらい精度が良くなったのか可視化してみようと思います。
内容としては前回の結果から、SVRのrbfモデルの正規化が一番スコアが良かったので、LinearRegressionモデルの正規化あるなしを基準として、SVR rbfモデルの正規化あるなしでどう予測値が変わるか見てみるという感じです。
ということでまずはデータの読み込みから。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果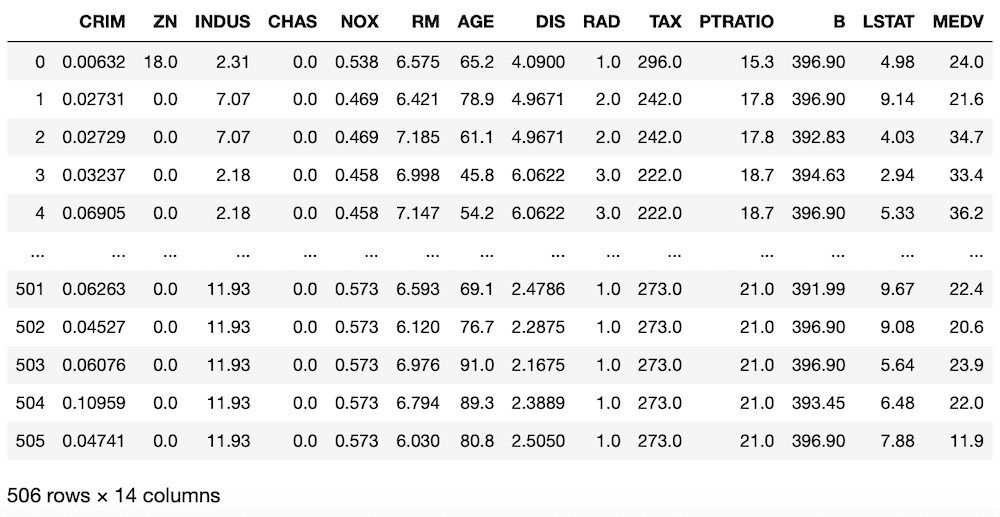
今回は正規化だけ使っていくので、次のセルはこんな感じ。
<セル2>
from sklearn.preprocessing import MinMaxScaler
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
norm_model = MinMaxScaler()
x_norm = norm_model.fit_transform(x)今回も犯罪率”CRIM”、平均部屋数”RM”、低所得者の割合”LSTAT”を使っていきます。
これで正規化あるなしの元データができました。
次から大きく変わっていくので、解説を交えてプログラムを作っていきましょう。
LinearRegressionとSVRで機械学習
次のセルでは先ほど作成した正規化あるなしの元データを学習用データセットとテスト用データセットに分けます。
その後、LinearRegressionモデルとSVR rbfモデルを使って機械学習させ、スコアを表示します。
まずはライブラリのインポートから。
データを分割する「train_test_split」、機械学習モデル「LinearRegression」と「SVR」、そしてスコアを計算する「r2_score」をインポートします。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.metrics import r2_score正規化あるなしそれぞれのデータを学習用データセットとテスト用データセットに分割します。
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
x_norm_train, x_norm_test, y_norm_train, y_norm_test = train_test_split(x_norm, y, test_size=0.2, train_size=0.8)それぞれのモデルと学習用データセットを使って機械学習させたのち、テスト用データセットでボストン住宅価格を予想し、予想精度のスコアを計算します。
model_lr = LinearRegression()
model_lr.fit(x_train, y_train)
pred_lr = model_lr.predict(x_test)
print(r2_score(y_test, pred_lr))
model_norm_lr = LinearRegression()
model_norm_lr.fit(x_norm_train, y_norm_train)
pred_norm_lr = model_norm_lr.predict(x_norm_test)
print(r2_score(y_norm_test, pred_norm_lr))
model_svr_rbf = SVR(kernel='rbf', gamma="scale")
model_svr_rbf.fit(x_train, y_train)
pred_svr_rbf = model_svr_rbf.predict(x_test)
print(r2_score(y_test, pred_svr_rbf))
model_norm_svr_rbf = SVR(kernel='rbf', gamma="scale")
model_norm_svr_rbf.fit(x_norm_train, y_norm_train)
pred_norm_svr_rbf = model_norm_svr_rbf.predict(x_norm_test)
print(r2_score(y_norm_test, pred_norm_svr_rbf))全部合わせるとこんな感じです。
<セル3>
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.metrics import r2_score
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
x_norm_train, x_norm_test, y_norm_train, y_norm_test = train_test_split(x_norm, y, test_size=0.2, train_size=0.8)
model_lr = LinearRegression()
model_lr.fit(x_train, y_train)
pred_lr = model_lr.predict(x_test)
print(r2_score(y_test, pred_lr))
model_norm_lr = LinearRegression()
model_norm_lr.fit(x_norm_train, y_norm_train)
pred_norm_lr = model_norm_lr.predict(x_norm_test)
print(r2_score(y_norm_test, pred_norm_lr))
model_svr_rbf = SVR(kernel='rbf', gamma="scale")
model_svr_rbf.fit(x_train, y_train)
pred_svr_rbf = model_svr_rbf.predict(x_test)
print(r2_score(y_test, pred_svr_rbf))
model_norm_svr_rbf = SVR(kernel='rbf', gamma="scale")
model_norm_svr_rbf.fit(x_norm_train, y_norm_train)
pred_norm_svr_rbf = model_norm_svr_rbf.predict(x_norm_test)
print(r2_score(y_norm_test, pred_norm_svr_rbf))
実行結果
0.6229646224173353
0.6319815322077402
0.5673322250620585
0.7654432098361073スコアとしては前回と同様、LinearRegressionでは正規化あるなしであまり違いはなく、SVR rbfモデルでは正規化することで大きく改善しています。
LinearRegressionモデルの結果をグラフ化してみる
それでは今回の目的である可視化をしてみましょう。
まずはLinearRegressionの結果をグラフにプロットしてみます。
今回はX軸を正解値、Y軸を予測値としてプロットします。
まずはmatplotlibのインポート、そしてjupyter notebook上で表示できるようマジックコマンドを入力します。
from matplotlib import pyplot as plt
%matplotlib inline次はグラフのプログラムを書いていきます。
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test, pred_lr, label="LR")
plt.scatter(y_norm_test, pred_norm_lr, label="LR_normalized")
plt.xlim(0, 55)
plt.ylim(0, 55)
plt.legend()「fig = plt.figure(figsize=(8,6))」でグラフサイズを規定しています。
「plt.clf()」でグラフエリアのクリア。
「plt.scatter(y_test, pred_lr, label=”LR”)
plt.scatter(y_norm_test, pred_norm_lr, label=”LR_normalized”)」でデータを散布図としてプロット。
「plt.xlim(0, 55)
plt.ylim(0, 55)」でX軸、Y軸の範囲を指定しています。
最後の「plt.legend()」で凡例の表示です。
合わせてみるとこんな感じになります。
<セル4>
from matplotlib import pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test, pred_lr, label="LR")
plt.scatter(y_norm_test, pred_norm_lr, label="LR_normalized")
plt.xlim(0, 55)
plt.ylim(0, 55)
plt.legend()
実行結果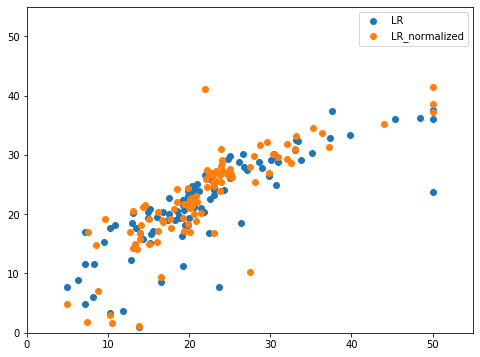
それではまずはこのデータを解析していきましょう。
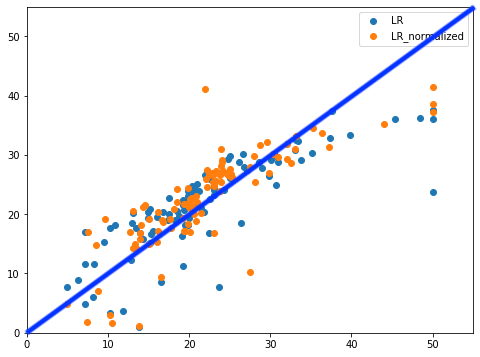
このデータの見方ですが、X軸に正解値、Y軸に予測値となっているので、斜めの直線(青線)に近いほど、正解に近いと言えます。
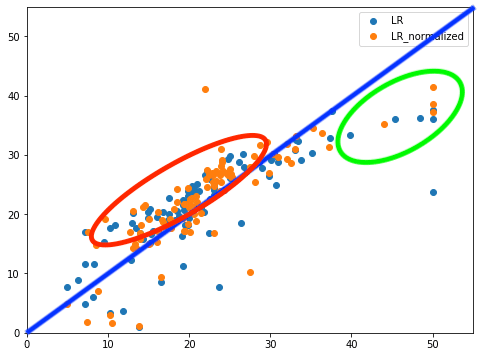
このLinerRegressionモデルの場合、10から20辺りの予想が少し高めに出てしまっており(赤丸)、また40から50辺りの予想が少し低めに出てしまっています(緑丸)。
SVR rbfモデルの結果をグラフ化してみる
それではSVR rbfモデルではどうでしょうか。
こちらもLinearRegressionモデルと同様にして、グラフ化してみましょう。
ただしmatplotlibはもうインポートしてあるので、ここでは記載する必要はありません。
ということでこんな感じ。
<セル5>
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test, pred_svr_rbf, label="SVR rbf")
plt.scatter(y_norm_test, pred_norm_svr_rbf, label="SVR rbf normalized")
plt.xlim(0, 55)
plt.ylim(0, 55)
plt.legend()
実行結果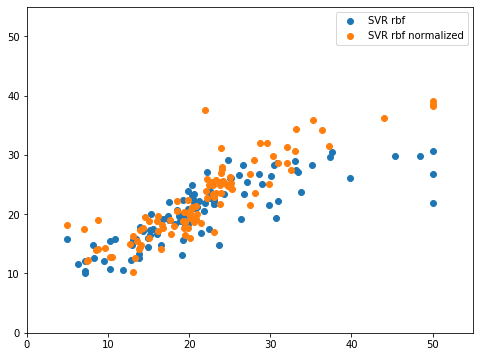
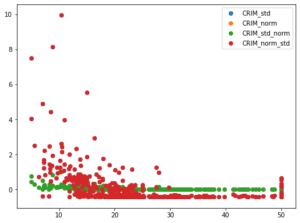
こちらも解析をしていきましょう。
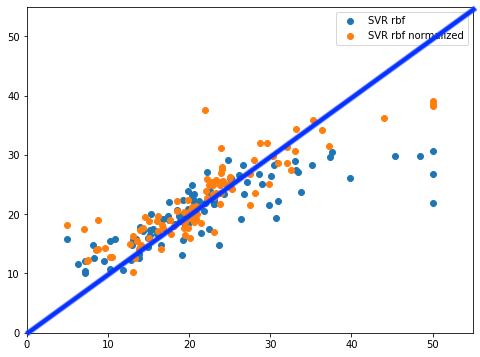
正解ラインを引いてみるとこんな感じ。
LinearRegressionモデルに比べると、正規化したSVR rbfモデル(橙色の点)ではラインに乗っているように見えます。
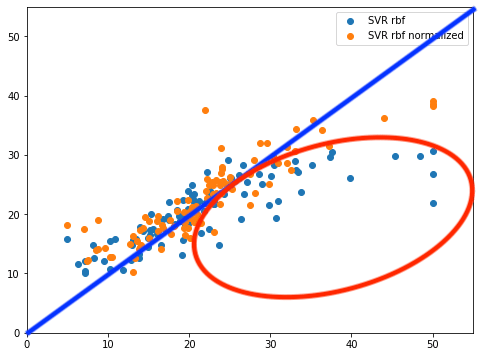
また正規化なしのSVR rbfモデルでは広範囲に渡って予想値が正解値よりも大幅に下振れしてしまっているのがわかります(赤丸)。
しかし正規化ありのSVR rbfモデルでは40〜50といった高価格帯では多少は下振れしていますが、大幅に改善していることがわかります。
これがスコアが良くなった理由であると言えるでしょう。
こういった数値を扱う分析では、数値が良くなったことに満足してしまい、中身が本当に良くなったのか確認せずに進めてしまうことが多々あります。
もちろん中身が改善されていないと、後々正しい分析ができなくなってしまい、全部やり直しなんてことになってしまいます。
プログラミングもそうですが、一つ一つ確認していくというのが重要なんですね。
標準化・正規化の効果が出ていて、それが予想精度に正しい影響を与えているということがわかりましたが、ちょっと疑問が浮かんできました。
これまでは標準化・正規化は別々にやってきましたが、両方やったら予想精度はどうなるのでしょうか?
ということで次回は標準化・正規化の両方をやった場合はどうなるのか試してみましょう。
ということで今回はこんな感じで。

コメント