【Scikit-learn】糖尿病患者のデータセットでLinearRegressionモデルのオプションを検討［Python］

2021年2月3日2022年12月9日

URLをコピーしました！

機械学習ライブラリScikit-learn

前回までは機械学習ライブラリScikit-learnの糖尿病患者のデータセットの読み込みから、ターゲットである1年後の糖尿病の進行と10個の特徴量の相関を見てみました。

あわせて読みたい

【Scikit-learn】糖尿病患者のデータセットを確認、相関マップを表示［Python］【機械学習ライブラリScikit-learn】前回までは機械学習ライブラリScikit-learnのボストン住宅価格のデータセットを使い、色々な機械学習モデル、標準化・正規化の効果…

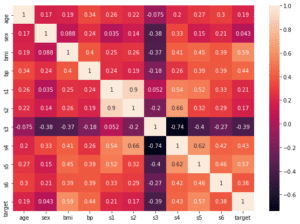
前回、データを確認したところで、この糖尿病患者のデータセットもボストン住宅価格のデータセットと同様に数値を予想するものなので、LinearRegression、Lasso、ElasticNet、Ridge、SVRのモデルを使えば良さそうだというお話をしました。

ということで今回は、上記の5つの機械学習のモデルの中からLinearRegressionに注目して、オプションを変えてみて、予想精度がどのように変わるか検討してみましょう。

ではではデータの読み込みから。

＜セル１＞

from sklearn.datasets import load_diabetes
import pandas as pd

diabetes = load_diabetes()

df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)

df["target"] = diabetes.target

df

実行結果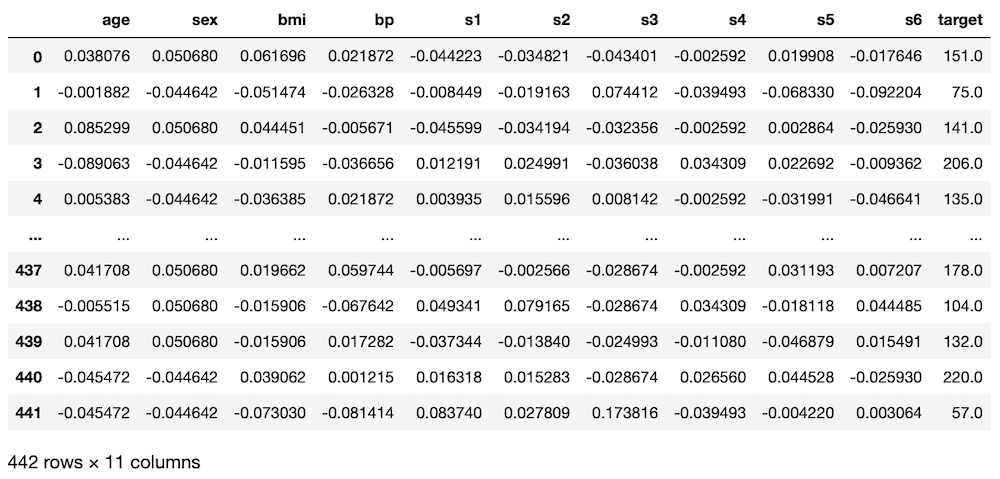

次に機械学習に用いる特徴量とターゲットを変数xとyにそれぞれ格納します。

前回、相関をみた結果、「bmi」、「s5」、「bp」、「s4」、「s3」あたりがターゲットと相関が高そうということだったので、それらをxに格納します。

（後で気付いたのですが、前の記事では「s6」も関連性がありそうということでしたが、忘れてしまいました。他の記事でも上記の組み合わせで行っているものもありますが、忘れたんだなぁと思って読んでください。）

＜セル２＞

x = df.loc[:, ["bmi", "s5", "bp", "s4", "s3"]]
y = df.loc[:, "target"]

次にデータ分割から、機械学習、ターゲットの推測を繰り返し行い、予想精度の平均スコアを計算します。

＜セル３＞

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

trial = 100

pred_lr_score = []; pred_lr_train_score = []

for i in range(trial):
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
    
    model_lr = LinearRegression()
    model_lr.fit(x_train, y_train)
    pred_lr = model_lr.predict(x_test)
    pred_lr_score.append(r2_score(y_test, pred_lr))
    
    pred_lr_train = model_lr.predict(x_train)
    pred_lr_train_score.append(r2_score(y_train, pred_lr_train))
    
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_lr_train_ave = np.average(np.array(pred_lr_train_score))
    
print(pred_lr_ave, pred_lr_train_ave)

実行結果
0.4624959484477522 0.49698708966015787

ここら辺のプログラムに関しては、ボストン住宅価格のデータセットを使った時に何度も使いましたので、解説は割愛します。

ただ一点、テスト用のデータだけではなく学習用のデータを使って、予想されるというプログラムを追加しました。

pred_lr_train = model_lr.predict(x_train)
pred_lr_train_score.append(r2_score(y_train, pred_lr_train))

理由としては「過学習」と呼ばれる学習用データに過剰に合わせてしまった状態をはんべつするためです。

つまり学習用のデータで予想した値のスコアがものすごく良く、テスト用のデータで予想した値のスコアが悪い場合、学習用のデータに合わせ過ぎた予想をしてしまっているというわけです。

今回はテスト用データでのスコアが「0.46250」で、学習用データでのスコアが「0.49699」であり、少しだけ学習用データのスコアが良かったくらいなので、過学習にはなっていないと考えられます。

機械学習の精度としては、ボストン住宅価格のデータセットの時よりも低い値が出てしまっています。

これがオプションを変えることでどのように変わっていくのか、ちょっと楽しみですね。

LinearRegressionのヘルプを見てみる

オプションを変えてみるといっても、どんなオプションがあるのか分かりません。

もちろんScikit-learnのウェブサイトに行けば、解説ページはあります。

scikit-learn

sklearn.linear_model.LinearRegression Examples using sklearn.linear_model.LinearRegression: Principal Component Regression vs Partial Least Squares Regression Plot individual and voting regression p…

ブラウザ開くのも面倒だ、検索かけるのも面倒だという方はhelp関数で調べてしまうという手もあります。

＜セル４＞

help(LinearRegression())

実行結果
Help on LinearRegression in module sklearn.linear_model._base object:

class LinearRegression(sklearn.base.MultiOutputMixin, sklearn.base.RegressorMixin, LinearModel)
 |  LinearRegression(*, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
 |  
 |  Ordinary least squares Linear Regression.
 |  
 |  LinearRegression fits a linear model with coefficients w = (w1, ..., wp)
 |  to minimize the residual sum of squares between the observed targets in
 |  the dataset, and the targets predicted by the linear approximation.
（以下略）

少しずつ下に進んでいくと、「Parameters」という項目が見つかります。

|  Parameters
 |  ----------
 |  fit_intercept : bool, default=True
 |      Whether to calculate the intercept for this model. If set
 |      to False, no intercept will be used in calculations
 |      (i.e. data is expected to be centered).
 |  
 |  normalize : bool, default=False
 |      This parameter is ignored when ``fit_intercept`` is set to False.
 |      If True, the regressors X will be normalized before regression by
 |      subtracting the mean and dividing by the l2-norm.
 |      If you wish to standardize, please use
 |      :class:`sklearn.preprocessing.StandardScaler` before calling ``fit`` on
 |      an estimator with ``normalize=False``.
 |  
 |  copy_X : bool, default=True
 |      If True, X will be copied; else, it may be overwritten.
 |  
 |  n_jobs : int, default=None
 |      The number of jobs to use for the computation. This will only provide
 |      speedup for n_targets > 1 and sufficient large problems.
 |      ``None`` means 1 unless in a :obj:`joblib.parallel_backend` context.
 |      ``-1`` means using all processors. See :term:`Glossary <n_jobs>`
 |      for more details.

ここの解説によるとLinearRegressionモデルのオプションは４つ。

fit_intercept: モデルでグラフの切片を使用するかしないか。Falseにするとグラフは必ず原点を通る。
bool値（TrueかFalseか）、デフォルト値はTrue

normalize: 値を正規化（ノーマライズ）するかどうか。
bool値（TrueかFalseか）、デフォルト値はFalse

copy_X: xの値をコピーして使用するか、上書きして使うか。
bool値（TrueかFalseか）、デフォルト値はTrue

n_jobs: 使用するジョブ数（CPU数）
int値（整数値）、デフォルト値はNone（ジョブ数１）

copy_Xとn_jobsはあくまでも計算のやり方を指示するものであり、計算結果に影響を与えるものではないようです。

ということで「fit_intercept」と「normalize」を試してみましょう。

fit_intercept

LinearRegression、つまり回帰直線を計算する際に傾きと切片を計算するのですが、このオプションで切片を計算するかしないかを変更できます。

デフォルト値はTrueなので、指定しないと「計算する」ということになります。

ということで先ほどの＜セル３＞のうち、

model_lr = LinearRegression()

が

model_lr = LinearRegression(fit_intercept=True)

か

model_lr = LinearRegression(fit_intercept=False)

になるということです。

まずは「True」を指定してみましょう。

＜セル３ fit_intercept=True＞

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

trial = 100

pred_lr_score = []; pred_lr_train_score = []

for i in range(trial):
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
    
    model_lr = LinearRegression(fit_intercept=True)
    model_lr.fit(x_train, y_train)
    pred_lr = model_lr.predict(x_test)
    pred_lr_score.append(r2_score(y_test, pred_lr))
    
    pred_lr_train = model_lr.predict(x_train)
    pred_lr_train_score.append(r2_score(y_train, pred_lr_train))
    
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_lr_train_ave = np.average(np.array(pred_lr_train_score))
    
print(pred_lr_ave, pred_lr_train_ave)

実行結果
0.4733664152677192 0.4943304142729141

Trueがデフォルトなので、指定しない場合とスコアは同じくらいになりました。

指定なし：0.4624959484477522
True指定：0.4733664152677192

またテスト用データでのスコアと学習用データでのスコアに大きな差がないので、過学習にはなっていないと考えられます。

次に「False」を指定してみます。

＜セル３ fit_intercept=False＞

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

trial = 100

pred_lr_score = []; pred_lr_train_score = []

for i in range(trial):
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
    
    model_lr = LinearRegression(fit_intercept=False)
    model_lr.fit(x_train, y_train)
    pred_lr = model_lr.predict(x_test)
    pred_lr_score.append(r2_score(y_test, pred_lr))
    
    pred_lr_train = model_lr.predict(x_train)
    pred_lr_train_score.append(r2_score(y_train, pred_lr_train))
    
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_lr_train_ave = np.average(np.array(pred_lr_train_score))
    
print(pred_lr_ave, pred_lr_train_ave)

実行結果
-3.559663306629671 -3.4134474255835268

結果は「-3.559663306629671」とあり得ない数値になってしまいました。

何がおかしいのか最後の学習で得られたデータをX軸を正解の数値、Y軸を予想の数値としてプロットしてみましょう。

＜セル４＞

from matplotlib import pyplot as plt

fig=plt.figure(figsize=(8,6))
plt.clf()

plt.scatter(y_test, pred_lr)

実行結果

fit_intercept=Trueの場合

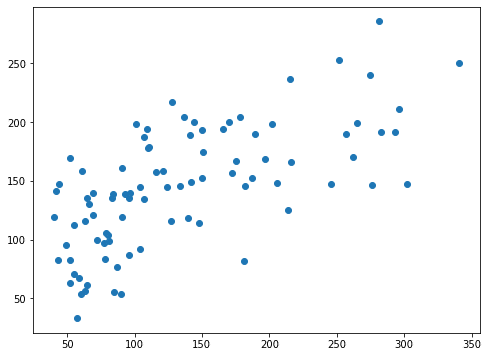
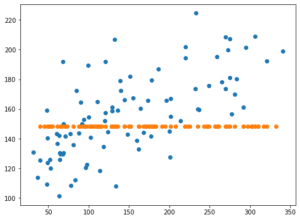
fit_intercept=Falseの場合

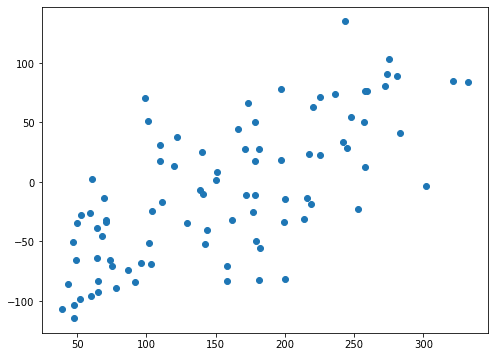
両方ともばらつきはあるものの、右肩上がりのプロットになっています。

しかしY軸の数値に注目してみてください。

fit_intercept=Falseの場合、-150くらいから150くらいの範囲になっています。

つまり予想した結果で得られた数値があっていないということになり、それがスコアに反映されたのだと考えられます。

このことから「fit_intercept」は特別な時を除き、「デフォルト値（True）」で使用すれば問題なさそうです。

normalize

次は「normalize」ですが、もうこの糖尿病患者のデータセットは「平均による中心化」の処理してあるデータセットなので、あまり効果がないかもしれません。

とりあえずやってみましょう。

normalizeはデフォルト値はFalseなので、指定しないと正規化しません。

＜セル３ normalized=False＞

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

trial = 100

pred_lr_score = []; pred_lr_train_score = []

for i in range(trial):
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
    
    model_lr = LinearRegression(normalize=False)
    model_lr.fit(x_train, y_train)
    pred_lr = model_lr.predict(x_test)
    pred_lr_score.append(r2_score(y_test, pred_lr))
    
    pred_lr_train = model_lr.predict(x_train)
    pred_lr_train_score.append(r2_score(y_train, pred_lr_train))
    
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_lr_train_ave = np.average(np.array(pred_lr_train_score))
    
print(pred_lr_ave, pred_lr_train_ave)

実行結果
0.4787054701181639 0.4931262872729931

デフォルト値と変わらないので、指定しない場合とスコアは似通った値になっています。

指定なし：0.4624959484477522
True指定：0.4787054701181639

次にnormalize = Trueとしてみましょう。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

trial = 100

pred_lr_score = []; pred_lr_train_score = []

for i in range(trial):
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
    
    model_lr = LinearRegression(normalize=True)
    model_lr.fit(x_train, y_train)
    pred_lr = model_lr.predict(x_test)
    pred_lr_score.append(r2_score(y_test, pred_lr))
    
    pred_lr_train = model_lr.predict(x_train)
    pred_lr_train_score.append(r2_score(y_train, pred_lr_train))
    
pred_lr_ave = np.average(np.array(pred_lr_score))
pred_lr_train_ave = np.average(np.array(pred_lr_train_score))
    
print(pred_lr_ave, pred_lr_train_ave)

実行結果
0.4677382349494845 0.4958438065432296

最初にお話しした通り、このデータセットは「平均による中心化」をしてあるデータなので、指定なしとあまりスコアは変わりませんでした。

指定なし：0.4624959484477522
True指定：0.4677382349494845

とりあえずLinearRegressionで予測精度に関わりそうな2つのオプションを紹介しました。

過学習にはならなかったものの残念ながら予測精度は上がらなかったので、次回はLassoモデルのオプションを色々いじっていきたいと思います。