機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnに含まれるボストンの住宅価格のデータセットを読み込み、大まかにデータを眺めてみました。
このボストンの住宅価格のデータでは、最終的にある条件の住宅の価格を予想したいので、今回は1つの特徴量データと住宅価格のデータでグラフを描いてみて、関連性があるか考えていきましょう。
ということで準備をしていきます。
前回、データを読み込み、Pandasのデータフレームに格納していますので、そこまではまとめた形にしてしまいましょう。
また今回もセルを変えていきますので、セル番号を振っておきます。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果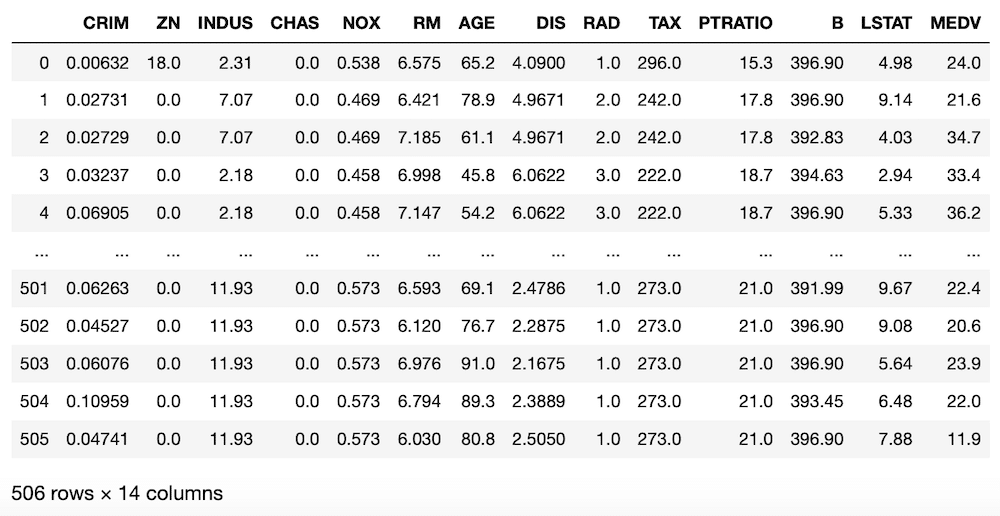
それではデータを可視化していきましょう。
グラフをseaborn jointplotで可視化:犯罪率(CRIM)vs 住宅価格(MEDV)
グラフとしてデータを可視化するのに、グラフ表示ライブラリ seabornを使っていきます。
その中でも今回は2つの要素をX軸、Y軸に描写したいので、jointplotを使っていきます。
そのためseabornをインポート、そしてマジックコマンドでjupyter notebook内でグラフ表示できるようにしておきます。
<セル2>
import seaborn as sns
%matplotlib inlineまずは犯罪率(CRIM)と住宅価格(MEDV)を使ってグラフ表示してみます。
<セル3>
sns.jointplot(x="CRIM", y="MEDV", data=df)
実行結果
X軸方向にCRIM(犯罪率)、Y軸方向にMEDV(住宅価格)となりました。
また上と右にヒストグラムが表示されています。
この犯罪率と住宅価格の場合、ほとんどの場合、犯罪率が低く抑えられています。
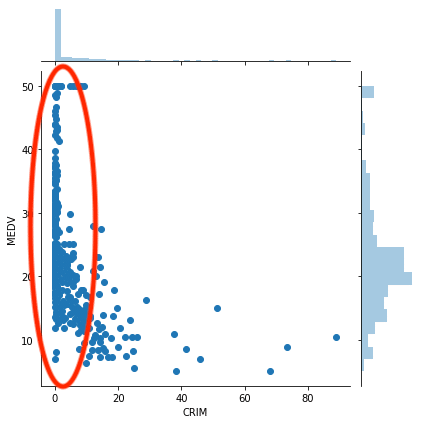
しかし犯罪率が高くなっているところを見ると、住宅価格が低価格のところに偏っているのが分かります。
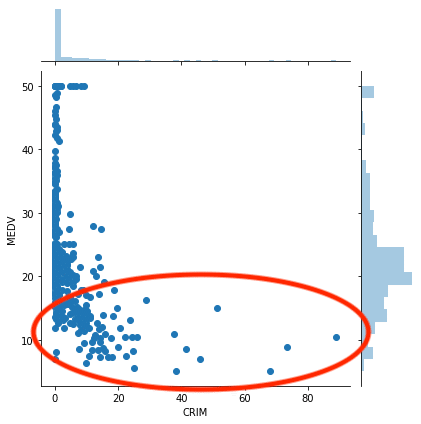
ということは犯罪率(CRIM)と住宅価格(MEDV)は関連性があると考えられます。
ではでは他の値に関しても見ていきましょう。
ZN(広い住宅区画の割合) vs 住宅価格(MEDV)
次に25,000平方フィート以上の住宅区画の割合(ZN)、つまりは区画に広い家を含むかどうかと住宅価格(MEDV)をjointplotを表示してみましょう。
<セル4>
sns.jointplot(x="ZN", y="MEDV", data=df)
実行結果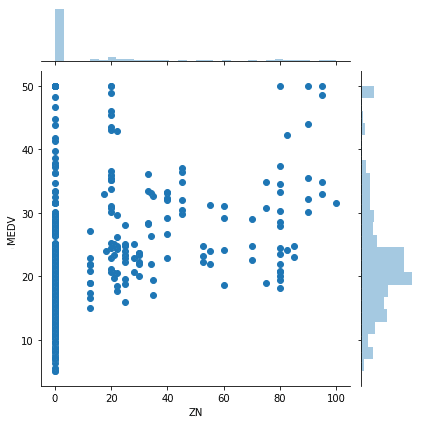
なんとなく見ていると、こんな感じで関連性があるように見えませんか?
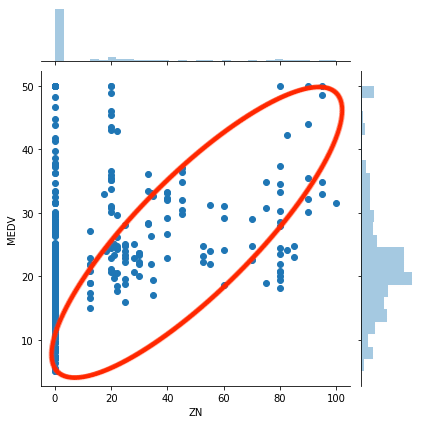
このように関連性が直線の場合、jointplotのオプションに「kind=”reg”」を追加すると、回帰直線を描いてくれます。
<セル4>
sns.jointplot(x="ZN", y="MEDV", data=df, kind="reg")
実行結果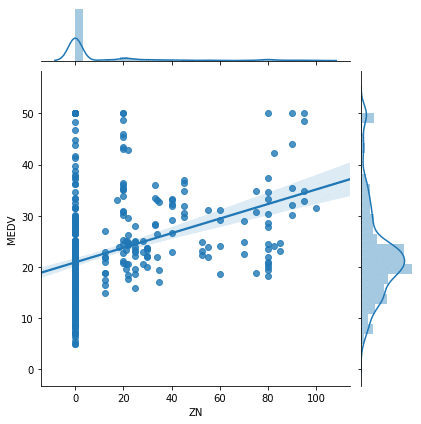
やっぱりなんとなく関連がありそうな感じはします。
ということで広い住宅を含む割合(ZN)も住宅価格(MEDV)と一応関連があるとしておきましょう。
INDUS(小売業以外の割合) vs 住宅価格(MEDV)
次は小売業以外のビジネスがされている土地の割合(INDUS)と住宅価格(MEDV)の関連性です。
<セル5>
sns.jointplot(x="INDUS", y="MEDV", data=df)
実行結果
この二つはこんな感じで関連性があるように見えますね。
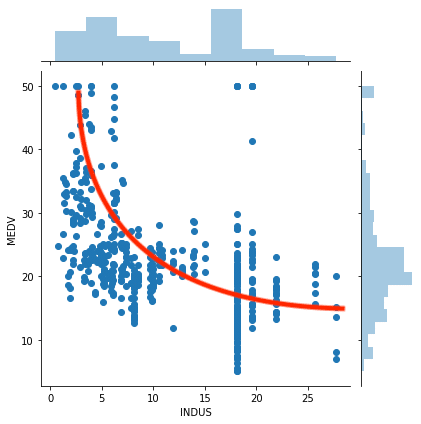
ということで小売業以外のビジネスがされている土地の割合(INDUS)と住宅価格(MEDV)も一応関連ありということで。
CHAS(チャールズ川沿いかどうか) vs 住宅価格(MEDV)
次は住宅がチャールズ川沿いかどうか(CHAS)と住宅価格(MEDV)の関連性です。
<セル6>
sns.jointplot(x="CHAS", y="MEDV", data=df)
実行結果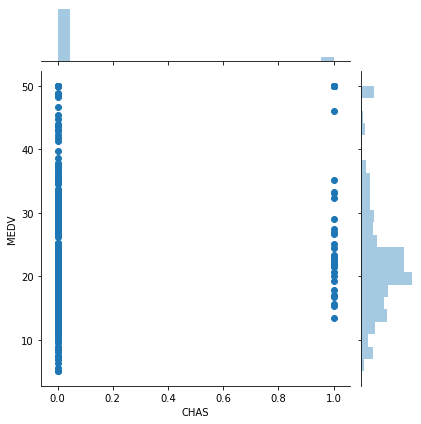
これは流石に厳しいでしょうか…一応、回帰直線を描いてみましょう。
<セル6 変更>
sns.jointplot(x="CHAS", y="MEDV", data=df, kind="reg")
実行結果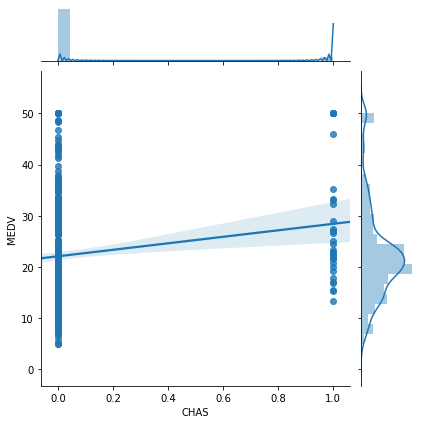
あまり傾きもないですし、関連性は無さそうです。
とりあえず現状では、住宅がチャールズ川沿いかどうか(CHAS)と住宅価格(MEDV)は関連がないということにしておきましょう。
NOX(窒素酸化物の濃度) vs MEDV(住宅価格)
次は地域の窒素酸化物の濃度(NOX)と住宅価格(MEDV)の関連性を見ていきます。
<セル7>
sns.jointplot(x="NOX", y="MEDV", data=df)
実行結果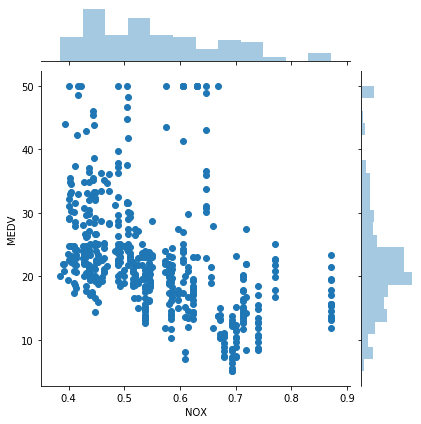
これはこんな感じで関連性がありそうです。
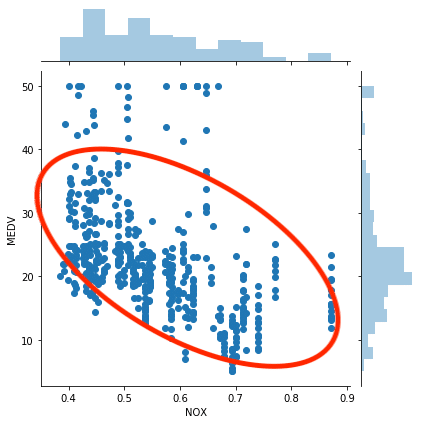
一応回帰直線も描いてみましょう。
<セル7 変更>
sns.jointplot(x="NOX", y="MEDV", data=df, kind="reg")
実行結果
やはり地域の窒素酸化物の濃度(NOX)と住宅価格(MEDV)は緩やかですが関連性がありそうですね。
RM(平均部屋数) vs MEDV(住宅価格)
次は平均部屋数(RM)と住宅価格(MEDV)です。
この組み合わせはデータの名前からしても関連性が高そうに見えます。
<セル8>
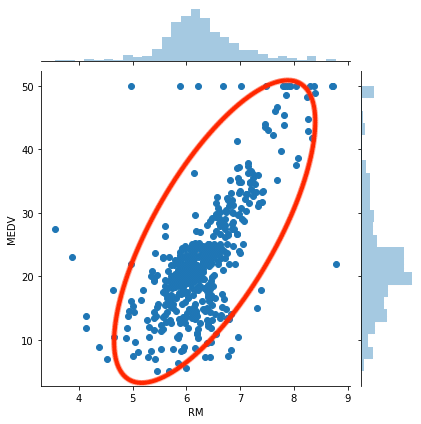
sns.jointplot(x="RM", y="MEDV", data=df)
実行結果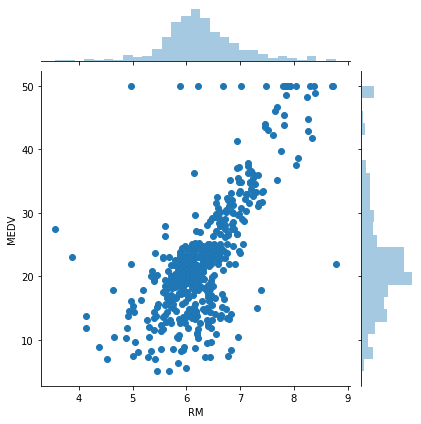
これはもう間違いなく、こんな感じで関連はありますね。
AGE(140年以上前に建てられた物件の割合) vs MEDV(住宅価格)
次は140年以上前に建てられて物件の割合(AGE)と住宅価格(MEDV)の関連性です。
<セル8>
sns.jointplot(x="AGE", y="MEDV", data=df)
実行結果
この領域を見ると、140年以上前の物件の割合が低いと住宅価格が低いように見えますが、
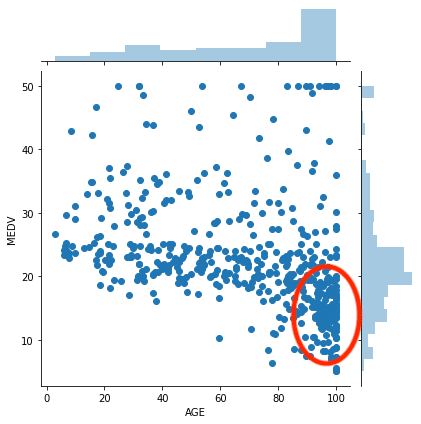
全体を見てみると、あまり一貫性がないように思えます。
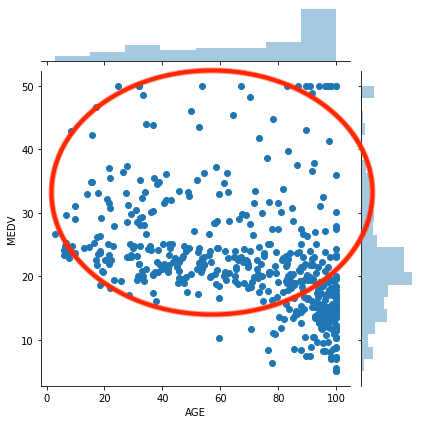
古くても部屋の広さや作りによって高い家もあるでしょうし、新しくても価格を抑えた住宅というのもあることでしょう。
ということで140年以上前に建てられて物件の割合(AGE)と住宅価格(MEDV)は関連性がないことも十分考えられます。
今回はデータに一貫性がないことと、古くても高い、新しくても安い住宅があることもあるという考えから、関連性がないとしておきましょう。
DIS(主要な職場からの距離) vs MEDV(住宅価格)
次はボストンの5つの主要な職場からの距離(DIS)と住宅価格(MEDV)の関連性です。
<セル9>
sns.jointplot(x="DIS", y="MEDV", data=df)
実行結果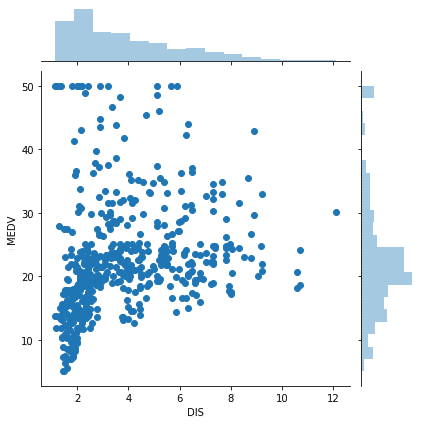
この場合は、職場に近いこの部分に着目すると、関連性がありそうに見えます。
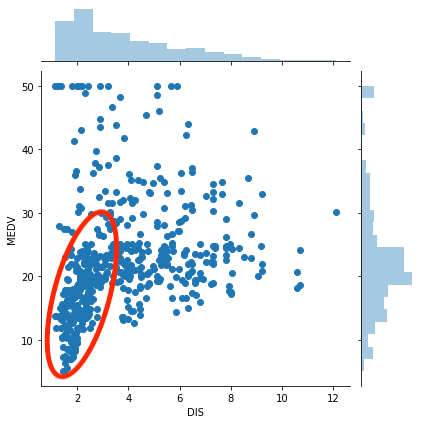
しかし全体を見ると、どんどん関連性が無くなっていっているのが分かります。
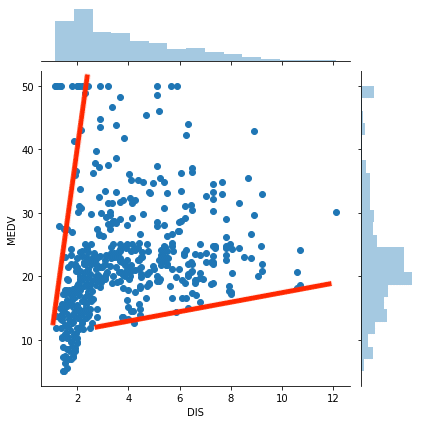
ちょっと判断に悩むところですが、とりあえずボストンの5つの主要な職場からの距離(DIS)と住宅価格(MEDV)の関連性はないとしておきましょう。
RAD(高速道路へのアクセスのしやすさ) vs MEDV(住宅価格)
次は高速道路へのアクセスのしやすさ(RAD)と住宅価格(MEDV)の関連性です。
<セル10>
sns.jointplot(x="RAD", y="MEDV", data=df)
実行結果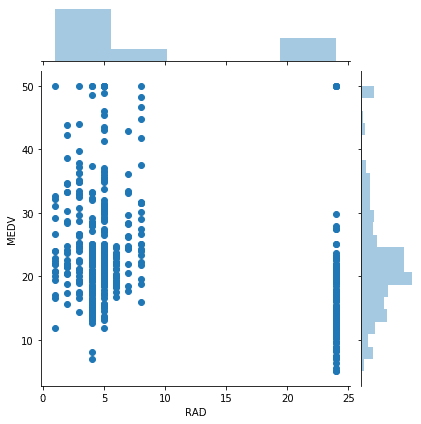
あくまでも高速道路へのアクセスのしやすさの指数で距離というわけではないので、飛び飛びの値になっているようです。
8くらいから24くらいに一気に飛んでいるのは気になりますが、一貫した傾向が見えないので、高速道路へのアクセスのしやすさ(RAD)と住宅価格(MEDV)は関連はないようです。
TAX($10,000あたりの住居に対する税率) vs MEDV(住宅価格)
次は$10,000あたりの住居に対する税率(TAX)と住宅価格(MEDV)の関連性です。
住居に対する税率ということは日本だと固定資産税になるのでしょうか。
<セル11>
sns.jointplot(x="TAX", y="MEDV", data=df)
実行結果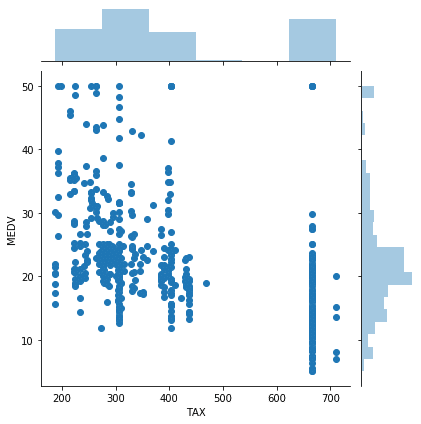
あまり固定資産税、というよりも税に関して詳しくないのですが、多分住宅が建っている場所の地価に対して税が変わると記憶しています。
ということは住宅価格には影響されないので、$10,000あたりの住居に対する税率(TAX)と住宅価格(MEDV)は関連性がなく、それがグラフにも現れているように見えます。
こういうこともあるので、データ解析を専門にする人は幅広い知識を身につける必要がありますね。
PTRATIO(生徒と教師の割合) vs MEDV(住宅価格)
次は生徒と教師の割合(PTRATIO)と住宅価格(MEDV)の関連性です。
これは生徒と教師の割合は教育レベルを表しているのでしょうか?
とりあえずグラフを表示してみましょう。
<セル12>
sns.jointplot(x="PTRATIO", y="MEDV", data=df)
実行結果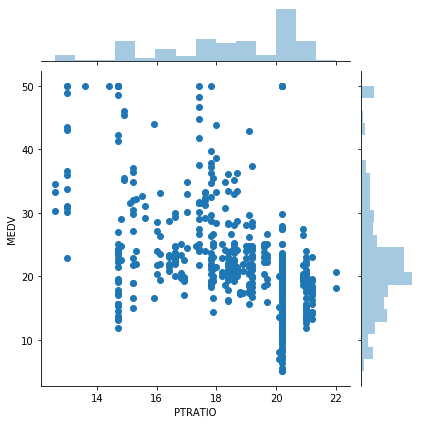
思ったより一貫性がないように見えます。
回帰直線を表示してみましょう。
<セル12 変更>
sns.jointplot(x="PTRATIO", y="MEDV", data=df, kind="reg")
実行結果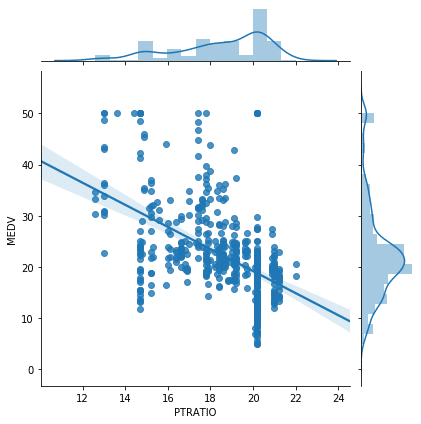
回帰直線を描いてみると、何となく関連性があるように見えますが、それでも何となくというレベルでしかありません。
ということで生徒と教師の割合(PTRATIO)と住宅価格(MEDV)の関連性はないとしておきましょう。
B(黒人の割合) vs MEDV(住宅価格)
次は黒人の割合(B)と住宅価格(MEDV)の関連性です。
<セル13>
sns.jointplot(x="B", y="MEDV", data=df)
実行結果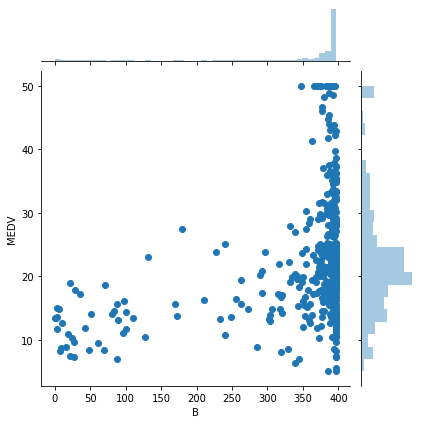
これはぱっと見で関連性はないと言えそうですね。
ということで今回は黒人の割合(B)と住宅価格(MEDV)の関連はないとしておきます。
LSTAT(低所得者の人の割合) vs MEDV(住宅価格)
次は低所得者の割合(LSTAT)と住宅価格(MEDV)の関連性です。
これは低所得者が多い地域では、住宅価格は低くなると予想できるので、関連性がありそうです。
<セル14>
sns.jointplot(x="LSTAT", y="MEDV", data=df)
実行結果
これは明らかに低所得者が少ない地域(つまり高所得者が多い地域)は住宅価格が高く、低所得者が多い地域は住宅価格が安いという相関がありそうです。
一応、回帰直線を描いてみましょう。
<セル14 変更>
sns.jointplot(x="LSTAT", y="MEDV", data=df, kind="reg")
実行結果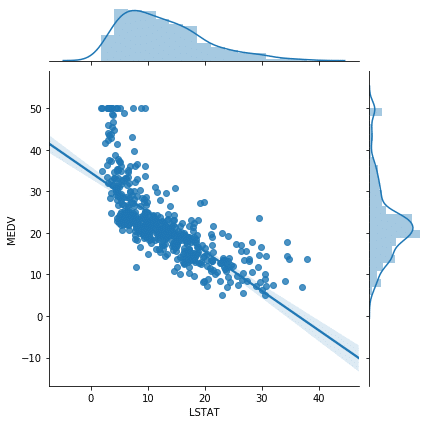
このグラフから分かるように、低所得者層の割合(LSTAT)と住宅価格(MEDV)の関連はあると言えます。
住宅価格と関連性がありそうな値のまとめ
ということでまとめていきましょう。
まず住宅価格と高い関連があると言えるのは、
- 犯罪率(CRIM)
- 平均部屋数(RM)
- 低所得者の割合(LSTAT)
またなんとなく関連がありそうなのは、
- 広い住宅区画の割合(ZN)
- 小売業以外のビジネスがされている土地の割合(INDUS)
- 窒素酸化物の濃度(NOX)
といった感じでしょうか。
ということで次回はこれらの値を使って機械学習を試してみましょう。
ではでは今回はこんな感じで。

コメント