機械学習ライブラリScikit-learn
前回まで機械学習ライブラリScikit-learnのワインの分類のデータセットの紹介をしました。
今回は「生理学データと運動能力の関係」のデータ セットを紹介していきます。
それでは始めていきましょう。
データセットの読み込み
まずはデータセットの読み込みをしていきます。
今回も手間を省くため、オプションを「as_Frame = True」としてPandasのデータセット形式で読み込みます。
<セル1>
from sklearn.datasets import load_linnerud
linnerud = load_linnerud(as_frame = True)
print(linnerud.keys())
実行結果
dict_keys(['data', 'feature_names', 'target', 'target_names', 'frame', 'DESCR', 'data_filename', 'target_filename'])とりあえずデータを表示させてみましょう。
<セル2>
linnerud.frame
実行結果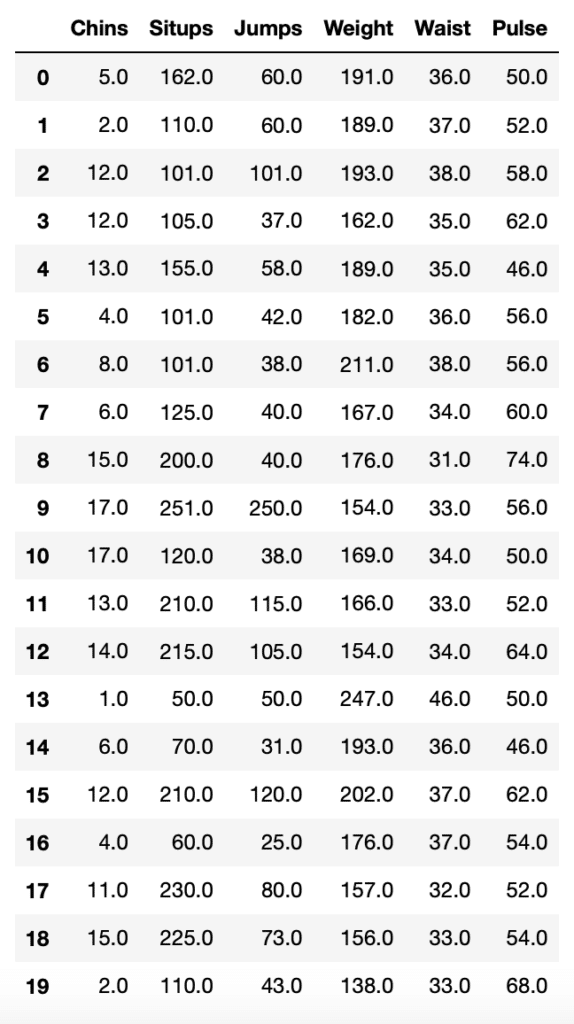
今回はかなり少ないデータ数ですね。
20個のデータに対し、6つの数値があります。
一番最後のデータが機械学習で予想する数値だとすると、5つの特徴量ということでしょうか。
データセットの概要を確認
ということで、DSCARをみてデータセットの概要を確認していきましょう。
<セル3>
print(linnerud.DESCR)
実行結果
.. _linnerrud_dataset:
Linnerrud dataset
-----------------
**Data Set Characteristics:**
:Number of Instances: 20
:Number of Attributes: 3
:Missing Attribute Values: None
The Linnerud dataset is a multi-output regression dataset. It consists of three
excercise (data) and three physiological (target) variables collected from
twenty middle-aged men in a fitness club:
- *physiological* - CSV containing 20 observations on 3 physiological variables:
Weight, Waist and Pulse.
- *exercise* - CSV containing 20 observations on 3 exercise variables:
Chins, Situps and Jumps.
.. topic:: References
* Tenenhaus, M. (1998). La regression PLS: theorie et pratique. Paris:
Editions Technic.「Number of Instances: 20」とあるので、データ数が20個なのはこのデータセットの仕様ですね。
「Number of Attributes: 3」とあり、実は特徴量は3であることが書かれています。
そして「The Linnerud dataset is a multi-output regression dataset.」とあり、予想すべき値が複数あると述べられています。
つまり「Chins(懸垂)」、「Situps(腹筋)」、「Jump(ジャンプ)」のそれぞれの数値から、「Weight(体重)」、「Waist(ウエスト)」、「Pulse(脈拍)」を予想すると言うことになります。
このように複数のターゲットをもつデータセットは初めてです。
とりあえず試していきましょう。
LinearRegressionで機械学習してみる
今回は回帰(Regression)のデータセットなので、とりあえず「LinearRegression」モデルを使って機械学習してみましょう。
またスコアの計算方法が前回と異なり、今回は「r2_score」を用います。
<セル4>
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
x = linnerud.frame.iloc[:, 0:2]
y = linnerud.frame.iloc[:, 3:6]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(r2_score(y_test, pred))重要なのはこちらの箇所。
x = linnerud.frame.iloc[:, 0:2]
y = linnerud.frame.iloc[:, 3:6]特徴量であるX値は最初の3列なので「linnerud.frame.iloc[:, 0:2]」となります。
そしてターゲットであるY値は後半の3列なので「linnerud.frame.iloc[:, 3:6]」です。
これで機械学習して、予想精度のスコアを算出させてみると、「-0.05673」となりました。
データ数が少ないのでスコアが低くても仕方がないかもしれません。
気になるのは、ターゲットの3つの数値をちゃんと予想できているのかということ。
ということで予想された数値を表示させてみましょう。
<セル5>
print(pred)
実行結果
[[166.01646478 33.38149009 57.38298545]
[195.56451799 37.9461248 52.77339858]
[187.28715426 36.83569489 53.90429319]
[164.8619361 33.12997491 57.63283437]]ちゃんと3つのターゲットを予想できていました。
今までこのように複数のターゲットをもつデータセットを試したことがなかったので、なかなか新鮮ですね。
それぞれのターゲットを別々に予想してみる
先ほどは3つのターゲットを一度に機械学習し、予想してみました。
その結果、スコアが「-0.05673」で、あまり相関がみられないという結果になってしまいました。
それではそれぞれ別に機械学習し、予想してみたらどうなるのでしょうか?
ということでまずは「weight」から試してみたいと思います。
<セル6>
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
x = linnerud.frame.iloc[:, 0:2]
y = linnerud.frame.iloc[:, 3]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(pred)
print(r2_score(y_test, pred))
実行結果
[185.84636463 197.41879316 158.9552652 189.84740172]
-0.3755780190997382先ほどよりは負の相関があるというスコアになりました。
次に「waist」です。
<セル7>
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
x = linnerud.frame.iloc[:, 0:2]
y = linnerud.frame.iloc[:, 4]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(pred)
print(r2_score(y_test, pred))
実行結果
[38.96764191 38.22306728 33.41278461 37.17811044]
-0.14959018354192288こちらもかなり低いですが、先ほどよりは負の相関があると言う結果になりました。
最後に「Pulse」。
<セル8>
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
x = linnerud.frame.iloc[:, 0:2]
y = linnerud.frame.iloc[:, 5]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
print(pred)
print(r2_score(y_test, pred))
実行結果
[51.99912493 52.43516477 50.98430881 53.89541582]
-0.3981429738231923これも同じく先ほどよりは負の相関があるいう結果ですね。
多分ですが、複数の値を予想するよりも、一つの値を予想する方が制限がなく、正解に近づくのではないかなと思います。
ただしターゲットとなる複数の値において、セットでなければいけない理由、今回で言えば一人の人から取得したデータであるという場合は一度に予想しなければいけないでしょう。
ということでやはりどうやって取得したデータなのか、何を知りたいのかということを頭にしっかりと刻んで機械学習をすることが重要なのかなと思います。
次回は最後の「乳がん患者のデータセット」を紹介します。
ではでは今回はこんな感じで。

コメント