機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnのボストンの住宅価格を犯罪率(CRIM)、平均部屋数(RM)、低所得者の割合(LSTAT)を使って機械学習させ、評価してみました。
今回はさらに関連性がありそうなこちらの3つのデータも追加して、精度を比較してみましょう。
- 広い住宅区画の割合(ZN)
- 小売業以外のビジネスがされている土地の割合(INDUS)
- 窒素酸化物の濃度(NOX)
ではではまずはデータを読み込んで、準備をしていきます。
<セル1>
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["MEDV"] = boston.target
df
実行結果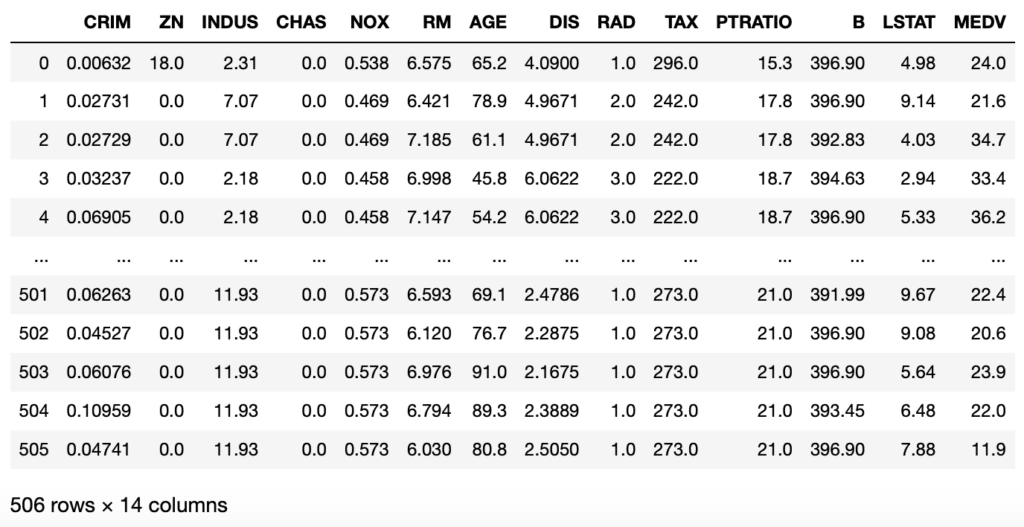
特徴量の異なるデータの準備とデータの分割
では特徴量の異なるデータを変数に格納して、訓練用データとテスト用データの分割をしていきましょう。
まずは前回のおさらいから。
from sklearn.model_selection import train_test_split
x = df.loc[:, ["CRIM", "RM", "LSTAT"]]
y = df.loc[:, "MEDV"]
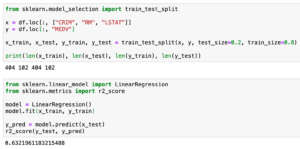
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
print(len(x_train), len(x_test), len(y_train), len(y_test))前回は犯罪率(CRIM)、平均部屋数(RM)、低所得者の割合(LSTAT)を変数xに、予想する値である住宅価格(MEDV)を変数yに格納しました。
そして「train_test_split」を使って、8割を訓練用データ、2割をテスト用データに分割しました。
今回はさらに広い住宅の割合(ZN)、小売以外のビジネスの土地の割合(INDUS)、窒素酸化物の濃度(NOX)を追加した変数を作成していきます。
x1 = df.loc[:, ["CRIM", "RM", "LSTAT"]]
x2 = df.loc[:, ["CRIM", "RM", "LSTAT", "ZN", "INDUS", "NOX"]]
y = df.loc[:, "MEDV"]変数x1に前回使用した3種のデータを格納し、変数x2にさらに3種追加した計6種のデータを格納しました。
変数yは前回同様、住宅価格(MEDV)を格納しています。
これを訓練用データ、テスト用データに分割するとこんな感じ。
<セル2>
from sklearn.model_selection import train_test_split
x1 = df.loc[:, ["CRIM", "RM", "LSTAT"]]
x2 = df.loc[:, ["CRIM", "RM", "LSTAT", "ZN", "INDUS", "NOX"]]
y = df.loc[:, "MEDV"]
x1_train, x1_test, y1_train, y1_test = train_test_split(x1, y, test_size=0.2, train_size=0.8)
x2_train, x2_test, y2_train, y2_test = train_test_split(x2, y, test_size=0.2, train_size=0.8)機械学習と評価をしてみる
それぞれのデータを使って機械学習させ、予想結果を評価してみましょう。
前回はこんな感じで機械学習・評価をしました。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
model = LinearRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
r2_score(y_test, y_pred)とりあえずこれを変数x1、変数x2に対して行っていきます。
<セル3>
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
model1 = LinearRegression()
model2 = LinearRegression()
model1.fit(x1_train, y1_train)
model2.fit(x2_train, y2_train)
y1_pred = model1.predict(x1_test)
y2_pred = model2.predict(x2_test)
print(r2_score(y1_test, y1_pred), r2_score(y2_test, y2_pred))
実行結果
0.6389382893844004 0.6558303567049748今回も決定係数を使っているので、予想値と正解値が近い場合は「1」に近くなり、遠い場合は「0」に近くなります。
3種の特徴量を使った場合は「0.638938」、6種の特徴量を使った場合は「0.655830」となりました。
ほんの少し良くなったでしょうか。
ただ1回だけの試行ではデータの分割のされ方によって、よく出てしまったり、悪く出てしまったりしてしまいます。
繰り返し検討できるようにプログラムを書き換える
ということでiris(アヤメ)のデータを使って機械学習した時と同様、繰り返し検討してみましょう。
変更の仕方はこちらの記事を参考にしてください。
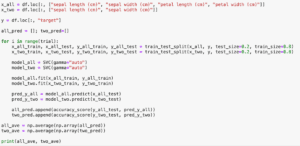
for文を使って、繰り返しデータ分割、モデルの作成と機械学習、予想と評価をして、その評価のスコアの平均を表示するという流れになります。
<セル3 変更>
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np
trial = 100
x1 = df.loc[:, ["CRIM", "RM", "LSTAT"]]
x2 = df.loc[:, ["CRIM", "RM", "LSTAT", "ZN", "INDUS", "NOX"]]
y = df.loc[:, "MEDV"]
pred1_score = []; pred2_score = []
for i in range(trial):
x1_train, x1_test, y1_train, y1_test = train_test_split(x1, y, test_size=0.2, train_size=0.8)
x2_train, x2_test, y2_train, y2_test = train_test_split(x2, y, test_size=0.2, train_size=0.8)
model1 = LinearRegression()
model2 = LinearRegression()
model1.fit(x1_train, y1_train)
model2.fit(x2_train, y2_train)
y1_pred = model1.predict(x1_test)
y2_pred = model2.predict(x2_test)
pred1_score.append(r2_score(y1_test, y1_pred))
pred2_score.append(r2_score(y2_test, y2_pred))
pred1_ave = np.average(np.array(pred1_score))
pred2_ave = np.average(np.array(pred2_score))
print(pred1_ave, pred2_ave)
実行結果
0.625231058778445 0.6134909009093165繰り返し試行して、どちらがいいか評価してみる
これでプログラムを変更できたので、前と同様100回試行して、平均値を出すというのを5回試してどちらのモデルがいいか検討してみましょう。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
| 3種の特徴量 | 0.62307 | 0.63860 | 0.62462 | 0.62526 | 0.63043 |
| 6種の特徴量 | 0.62010 | 0.60731 | 0.62194 | 0.62377 | 0.61287 |
6種の特徴量を使った時は多少は良くなるかと思ったのですが、全くスコアは上がりませんでした。
ということは今回追加した広い住宅の割合(ZN)、小売以外のビジネスの土地の割合(INDUS)、窒素酸化物の濃度(NOX)は住宅価格と関連性が低い、もしくはないということだと思います。
iris(アヤメ)のデータセットの場合は、正解率が97%程度あったので、十分機械学習の精度が出ていました。
今回は決定係数ということで単純に正解率と比較はできませんが、完全に予想値と正解値が一致している「1」からまだまだ遠いので十分な精度があるとは言えません。
今回は残念な結果ですが、単純に特徴量の種類を増やすだけでは機械学習の精度は上がらないというのが実感できました。
次回はまずは機械学習の手法を変えてみて、検証してみたいと思います。
ということで今回はこんな感じで。

コメント