Django
前回、二次関数表示アプリを作成するための準備を行いました。

今回は二次関数を計算して、グラフ化する部分のプログラムを構築していきます。
プログラムを書いていくのは、/webapp/quadraticfunction/views.pyです。
最初にプログラム全体を見せてしまうとこんな感じです。
from django.shortcuts import render
from django.http import HttpResponse
from .forms import QFForm
import matplotlib
matplotlib.use('Agg')
from matplotlib import pyplot as plt
import sys
sys.path.append('../')
from webapp import definitions
def plotting(a, b, c, xmax, xmin, ymax, ymin):
xlist = range(xmin, xmax+1)
ylist = []
for i in xlist:
ylist.append(a * i * i + b * i + c)
str_a = checksign(a); str_b = checksign(b); str_c = checksign(c)
if a == 0:
if b == 0:
eq = f'y={str_c[0]}'
elif b != 0:
eq = f'y={str_b[1]}x{str_c[2]}'
elif a != 0:
if b == 0:
eq = f'y={str_a[1]}x2{str_c[2]}'
elif b != 0:
eq = f'y={str_a[1]}x2{str_b[3]}x{str_c[2]}'
fig = plt.figure()
plt.clf()
plt.plot(xlist, ylist)
plt.grid()
plt.title(eq,{'fontsize':25})
plt.xlabel("X", {'fontsize':15})
plt.ylabel("Y", {'fontsize':15})
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.savefig("./quadraticfunction/static/quadraticfunction/quadraticfunction.png")
def checksign(val):
if val == 0:
return '0','','',''
elif val == 1:
return '1','','+1','+'
elif val == -1:
return '-1','-','-1',"-"
elif val > 0:
return f'{val}',f'{val}',f'+{val}',f'+{val}'
elif val < 0:
return f'{val}',f'{val}',f'{val}',f'{val}'
def index(request):
params = definitions.readjson()
initial_val = {
'a':1,
'b':0,
'c':0,
'xmin':-10,
'xmax':10,
'ymin':-10,
"ymax":10,
}
params['forms']= QFForm(request.POST or None, initial=initial_val)
plotting(initial_val['a'], initial_val['b'],initial_val['c'], initial_val['xmax'], initial_val['xmin'], initial_val['ymax'], initial_val['ymin'])
if (request.method == 'POST'):
a = int(request.POST['a'])
b = int(request.POST['b'])
c = int(request.POST['c'])
xmax = int(request.POST['xmax'])
xmin = int(request.POST['xmin'])
ymax = int(request.POST['ymax'])
ymin = int(request.POST['ymin'])
params['forms'] = QFForm(request.POST)
plotting(a, b, c, xmax, xmin, ymax, ymin)
return render(request, 'quadraticfunction/index.html', params)
plotting関数
今回の修正点で重要なのは一次関数表示アプリの際に作成したplotting関数です。
ここを二次関数用に修正していきます。
まずはplotting関数の引数に「c」を追加します。
def plotting(a, b, c, xmax, xmin, ymax, ymin):次に計算を行なっている部分。
xlist = range(xmin, xmax+1)
ylist = []
for i in xlist:
ylist.append(a * i * i + b * i + c)xの最大値、最小値から、x値のリスト(xlist)を作り、それをfor文で一つずつ取り出し、計算し、ylistに格納します。
「a * i * i + b * i + c」が \(y=ax^2+bx+c\) の計算を行なっている部分です。
次に式を表示する際の場合わけの部分です。
今回は前回とは違う形で場合わけを行っています。
その部分のプログラムを説明する前に新しい関数「checksign」を解説する必要があるので、先に解説します。
checksign関数はこんな感じです。
def checksign(val):
if val == 0:
return '0','','',''
elif val == 1:
return '1','','+1','+'
elif val == -1:
return '-1','-','-1',"-"
elif val > 0:
return f'{val}',f'{val}',f'+{val}',f'+{val}'
elif val < 0:
return f'{val}',f'{val}',f'{val}',f'{val}'何をやっているかというと、まず引数として数字「val」を入力します。
valが0、1、−1、0より大きい、0より小さい時で場合わけし、式の表示で使用する形に変換しています。
まとめてみるとこんな感じです。
| val | 出力[0] | 出力[1] | 出力[2] | 出力[3] |
| 0 | ‘0’ | ” | ” | ” |
| 1 | ‘1’ | ” | ‘+1’ | ‘+’ |
| -1 | ‘-1’ | ‘-‘ | ‘-1’ | ‘-‘ |
| >0 | f'{val}’ | f'{val}’ | f’+{val}’ | f’+{val}’ |
| <0 | f'{val}’ | f'{val}’ | f'{val}’ | f'{val}’ |
| 符号 | +なし -あり | +なし -あり | +あり -あり | +あり -あり |
| 0 | あり | なし | なし | なし |
| 1 | あり | なし | あり | なし |
f{‘変数名’}という書き方はこちらの記事で解説していますので、良かったらご覧ください。
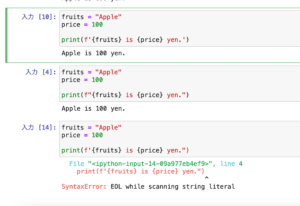
何故このような関数を作ったかというと、例えばxの前、つまりa、bの係数の「1」は省略しなければいけないけども、cに「1」が来た時は表示しなければいけない。
また数字の符号によって足し算なのか引き算なのかを変化させる、つまり \(y=2x+2)\ のcの位置の「2」には「+」が必要だけど、bの位置の「2」には「+」は必要ない。
こういう複雑な「0」「1」「+」「-」に対応できるように関数を作ったというわけです。
リスト形式で返ってくるので、どの形式を使いたいかインデックスで指定して使います。
この「checksign関数」を使って、式を作成するための部分はこのようにしました。
str_a = checksign(a); str_b = checksign(b); str_c = checksign(c)
if a == 0:
if b == 0:
eq = f'y={str_c[0]}'
elif b != 0:
eq = f'y={str_b[1]}x{str_c[2]}'
elif a != 0:
if b == 0:
eq = f'y={str_a[1]}x2{str_c[2]}'
elif b != 0:
eq = f'y={str_a[1]}x2{str_b[3]}x{str_c[2]}'ここで重要なのは「a」、「b」、「c」がそれぞれ「0」になる場合で式の形式が異なるため、場合わけする必要があるということです。
これで表示するための式は完成しました。
plotting関数の残りの部分はmatplotlibでグラフを作成する部分で、前回から変更はないので解説は割愛します。
fig = plt.figure()
plt.clf()
plt.plot(xlist, ylist)
plt.grid()
plt.title(eq,{'fontsize':25})
plt.xlabel("X", {'fontsize':15})
plt.ylabel("Y", {'fontsize':15})
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.savefig("./quadraticfunction/static/quadraticfunction/quadraticfunction.png")index関数
次にindex関数の部分を修正していきます。
一つ目の変更点はplotting関数の引数に「c」が追加されているため、plotting関数を使用している2カ所を修正します。
まずは初期値を使ってプロットする部分。
plotting(initial_val['a'], initial_val['b'],initial_val['c'], initial_val['xmax'], initial_val['xmin'], initial_val['ymax'], initial_val['ymin'])次に入力された値を使ってプロットする部分(if (request.method == ‘POST’):の後)。
plotting(a, b, c, xmax, xmin, ymax, ymin)また入力された値を取得する部分に「c」の値を取得するプログラムがないので追加します。
if (request.method == 'POST'):
a = int(request.POST['a'])
b = int(request.POST['b'])
c = int(request.POST['c'])
xmax = int(request.POST['xmax'])
xmin = int(request.POST['xmin'])
ymax = int(request.POST['ymax'])
ymin = int(request.POST['ymin'])これでサーバーを起動し、ブラウザでアクセスし、適当な数字を入れてみました。
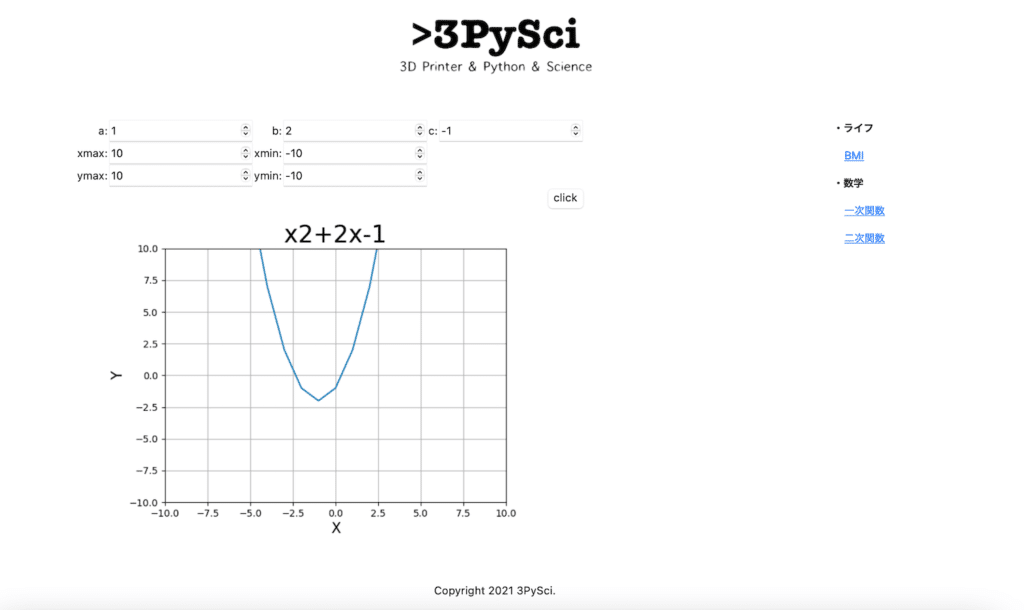
二次関数が表示されました。
いろいろ試してみたのですが、グラフも式も大きな問題はなさそうです。
ただまだまだ残念な点もあります。
一つ目として式の中の \(x^2\) の二乗が上付きになっていません。
二つ目として二次関数の重要な点として、頂点がありますが、その値が表示されていないことです。
次回はこれらを修正していきたいと思っていたのですが、少し他のバグが出ていたので、その修正を行います。
ではでは今回はこんな感じで。

コメント