Kaggle
前回は機械学習・データサイエンスのプラットフォーム「Kaggle(カグル)」の「タイタニック号乗客の生存予測」のデータセットのAgeの欠損値を機械学習でなんとかしようとして失敗しました。
今回からはもう少し真面目に、データを解析していって、Ageの欠損値を埋めていきたいと思います。
ただそのためにはまずはどういう方針でいくのか、方向性を決める必要があります。
今回はそのための情報収集をしてみましょう。
ということでまずはデータの読み込みとこれまでの修正を行っていきます。
<セル1>
import pandas as pd
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
train.loc[train["Sex"] == "male", "Sex"] = 0
train.loc[train["Sex"] == "female", "Sex"] = 1
test.loc[test["Sex"] == "male", "Sex"] = 0
test.loc[test["Sex"] == "female", "Sex"] = 1
test.loc[test["Fare"].isnull() == True, "Fare"] = 7.8875
train.loc[train["Embarked"].isnull() == True, "Embarked"] = "S"
train.loc[train["Embarked"] == "S", "Embarked"] = 0
train.loc[train["Embarked"] == "C", "Embarked"] = 1
train.loc[train["Embarked"] == "Q", "Embarked"] = 2
test.loc[test["Embarked"] == "S", "Embarked"] = 0
test.loc[test["Embarked"] == "C", "Embarked"] = 1
test.loc[test["Embarked"] == "Q", "Embarked"] = 2
all_data = pd.concat([train.drop(columns = "Survived"), test])
all_data
実行結果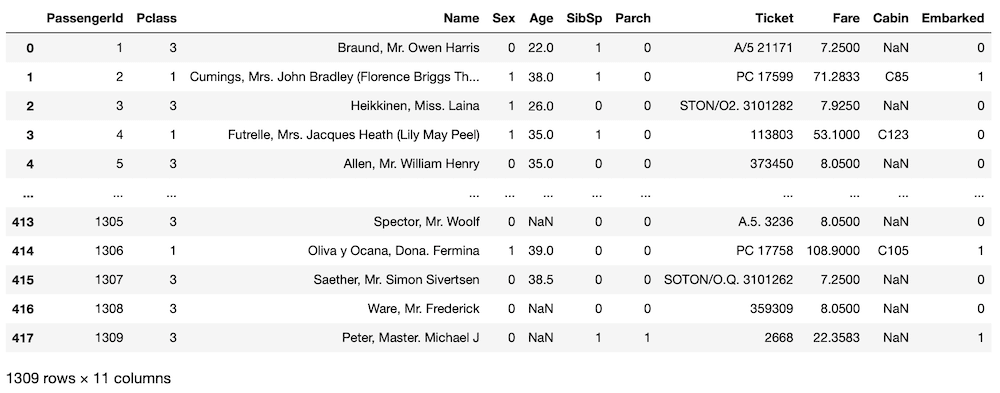
そして今回はもう一つ、Ageが欠損値になっているデータをまとめておきましょう。
<セル2>
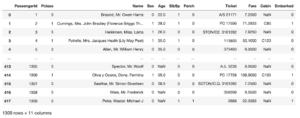
Age_no = all_data[all_data["Age"].isnull() == True]
Age_no
実行結果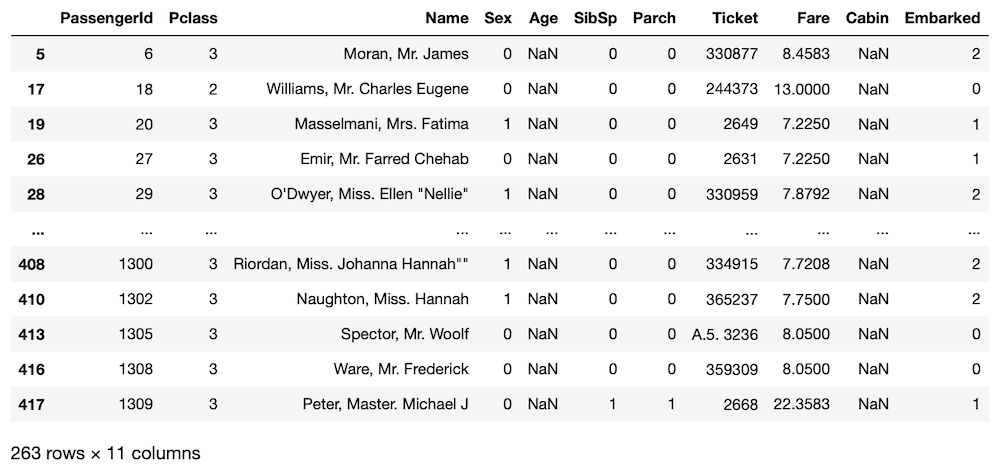
これで準備は完了です。
ここから色々と探っていきましょう。
仮説を立てる
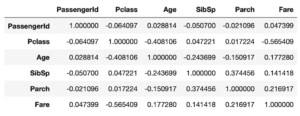
まずはデータを眺めながら、タイタニック号の乗客をイメージし、どの特徴量がAge(年齢)と関連しそうか一つ一つ考えていきます。
Pclass(チケットの等級)の仮説:年齢が上がるほど、収入や貯金が増え、より良い等級のチケットを購入しているのではないだろうか?
Name(名前)の仮説:結婚している女性はMrs.になるからそこから年齢が予想できるのではないか?逆にMissなら若い人が多いかもしれない。男性は敬称(Mr.とかDr.、Master等)で年齢が推測できるかもしれない。
SibSp(兄弟姉妹、配偶者の人数)の仮説:兄弟姉妹と配偶者では意味合いが大きく異なる。配偶者なら少なくとも成人しているが、兄弟姉妹だと若年層の可能性もある。見分けられたら、年齢を決める一つの情報になりうるのではないだろうか?
Parch(親・子供の数)の仮説:これも親なのか、子供なのか見分けれたら年齢を決める良い情報になりえる。
Ticket(チケット番号)の仮説:これだけでは年齢に結びつけるのは難しい。しかしSibSpやParchのサブ情報としては使えるかもしれない。
Fare(料金)の仮説:こちらも年齢に直接結びつけるのは難しい。
なんとなくAgeと関連があるか考えてみましたが、こんな感じでしょうか。
この中でも今回は最初の「Pclass」と「Age」の関係を探っていきたいと思います。
PclassとAgeの関係性を探る
PclassとAgeの関係を探るため、それぞれPclassにおけるAgeの分布を表示してみます。
比較用にまずはPclassの指定をしない場合はこちら。
<セル3>
all_data["Age"].hist()
実行結果
次にPclassが「1」の人の年齢分布。
<セル4>
all_data[all_data["Pclass"] == 1]["Age"].hist()
実行結果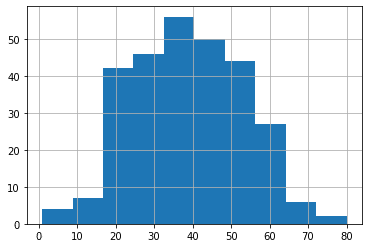
Pclassが「2」の人の年齢分布。
<セル5>
all_data[all_data["Pclass"] == 2]["Age"].hist()
実行結果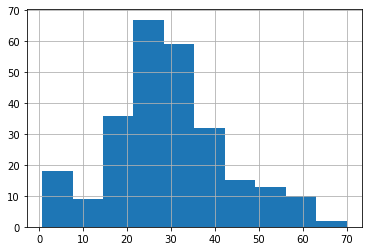
最後にPclassが「3」の人の年齢分布。
<セル6>
all_data[all_data["Pclass"] == 3]["Age"].hist()
実行結果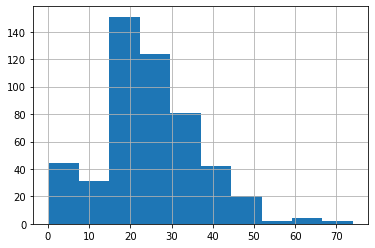
これらのグラフを比較してみると、Pclassが「3」の人の年齢分布が、全体の年齢分布と似通っているのが分かります。
そしてPclassが「1」と「2」においては全体の年齢分布とは異なり、それぞれ異なる年齢分布となっています。
つまりPclass「1」と「2」では、Pclassで分類することが意味があり、Pclassが「3」には意味がない、もしくは少ないことだと考えられます。
ここでAgeが欠損している人のPclassの分布を見てみましょう。
<セル7>
Age_no["Pclass"].hist()
実行結果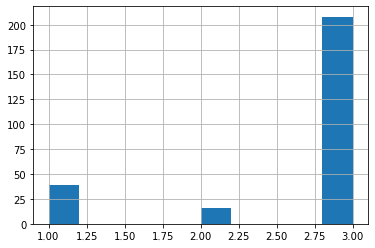
ついでにそれぞれ別のデータセットに分割して、データ数を数えてみます。
<セル8>
Age_no_1 = Age_no[Age_no["Pclass"] == 1]
Age_no_2 = Age_no[Age_no["Pclass"] == 2]
Age_no_3 = Age_no[Age_no["Pclass"] == 3]
print(len(Age_no_1))
print(len(Age_no_2))
print(len(Age_no_3))
実行結果
39
16
208Pclassが「1」と「2」のデータはそれぞれ39個と16個と欠損しているデータ数263個からするとそれほど多くはないです。
Pclassが「3」のデータは208個であり、これが欠損値の大半を占めています。
ということはPclassが「1」と「2」でAgeのデータが欠損しているものに対しては、先ほどの全体の年齢分布を当てはめても良さそうですが、Pclassが「3」のものに関してはもう少し分類が必要な気がします。
次回は別の見方に焦点を当てて、さらに考察を進めていきましょう。
ではでは今回はこんな感じで。

コメント