機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnの糖尿病患者のデータセットを使い、SVRモデルでkernelをrbf中心に色々と試してみました。
今回は”sigmoid”に関連するオプションを見ていきたいと思います。
ということでまずはデータの読み込みから。
<セル1>
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df["target"] = diabetes.target
df
実行結果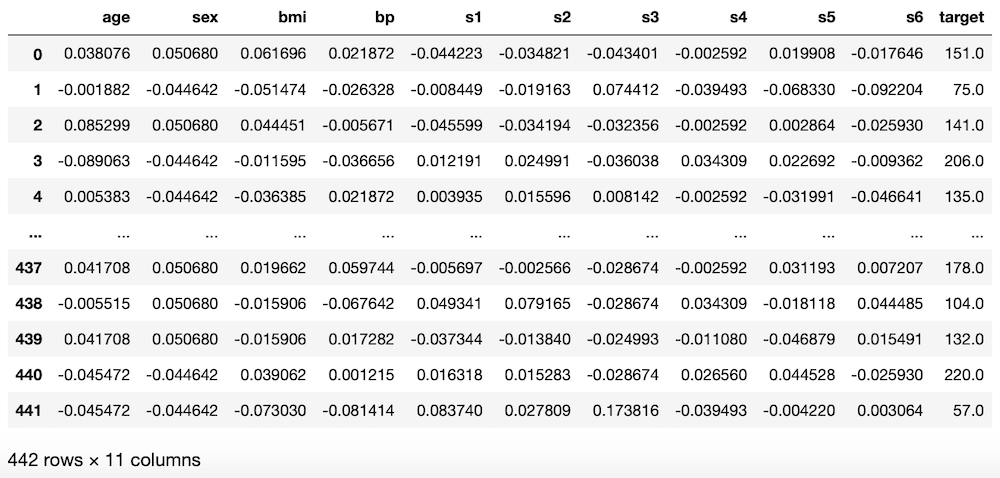
次に機械学習に用いる特徴量とターゲットをそれぞれ変数xとyに格納します。
(後で気付いたのですが、前の記事では「s6」も関連性がありそうということでしたが、忘れてしまいました。他の記事でも上記の組み合わせで行っているものもありますが、忘れたんだなぁと思って読んでください。)
<セル2>
x = df.loc[:, ["bmi", "s5", "bp", "s4", "s3"]]
y = df.loc[:, "target"]
実行結果次にSVRモデル読み込み、機械学習と予想を100回試した後、その予想精度のスコアの平均値を表示します。
この際、SVRのkernelをsigmoidに指定します。
また過学習になっていないか確認するため、テスト用データでのスコアだけでなく、学習用データでのスコアも計算します。
<セル3>
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train_ori, x_test_ori, y_train_ori, y_test_ori = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid")
model_svr.fit(x_train_ori, y_train_ori)
pred_svr_ori = model_svr.predict(x_test_ori)
pred_svr_score.append(r2_score(y_test_ori, pred_svr_ori))
pred_svr_ori_train = model_svr.predict(x_train_ori)
pred_svr_train_score.append(r2_score(y_train_ori, pred_svr_ori_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
0.40189367844128376 0.4120729668270072そしてグラフの表示です。
<セル4>
from matplotlib import pyplot as plt
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
実行結果
ということでkernel=”sigmoid”に関連するオプションを見ていきましょう。
解説ページからすると、「gamma」と「coef0」が”sigmoid”に関連するようです。

「gamma」は前回、kernel=”rbf”の時に試しているので、今回は「coef0」を試してみることにします。
coef0
coef0: カーネル関数とは独立した項(?)。”poly”と”sigmoid”においてのみ意味を持つ。
float値(小数)、デフォルト値は0.0
これまたよく分からない値です。
とりあえず”poly”と”sigmoid”の時だけ使用できる値であるということだけは分かりました。
デフォルト値は0.0らしいので、まずは負の値が使えるかどうかの確認をしてみます。
ということでまずはcoef0=-1を試してみましょう。
<セル5 coef0=-1>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=-1)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
0.3771579626675715 0.3874905934987896負の値も使うことができました。
スコア的には指定なしの「0.40189」よりもほんの少し悪くなったかなという感じですね。
グラフはどうでしょうか。
<セル6 coef0=-1>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果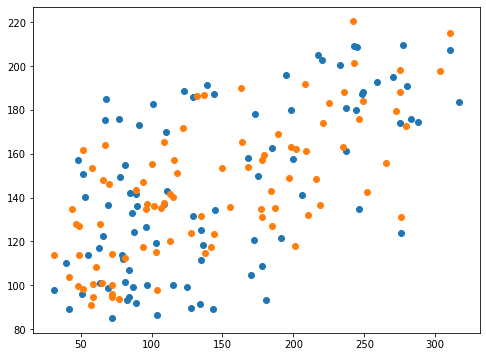
グラフ的にはあまり変わったように見受けられません。
では正の値はどうでしょうか。
coef0=1を試してみましょう。
<セル5 coef0=1>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=1)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
0.33454221936314604 0.35578786905343385指定なしの「0.40189」で、coef0=-1の時のスコアが「0.37716」なのでまた悪くなってしまいました。
<セル6 coef0=1>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果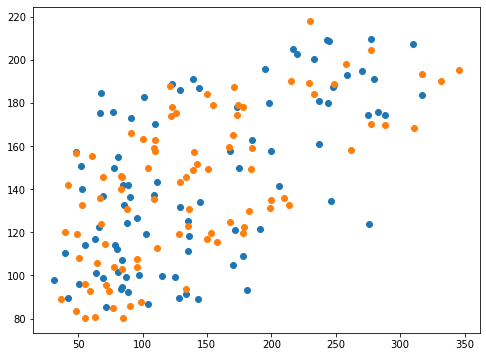
グラフはあまり変わったように見えませんが、これでもスコアに大きく影響しているのですね。
coef0の値をもっと大きくしたらどうなるでしょうか?
ということで次はcoef0=10を試してみます。(以下2021/3/26修正)
<セル5 coef0=10>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=10)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
-0.04221676686209951 -0.02455321960174181スコアは今回最高値が出てきました。
スコアはマイナスという全く合っていないという値になりました。
予想値はどう変わったのか、グラフで確認してみましょう。
<セル6 coef=10>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果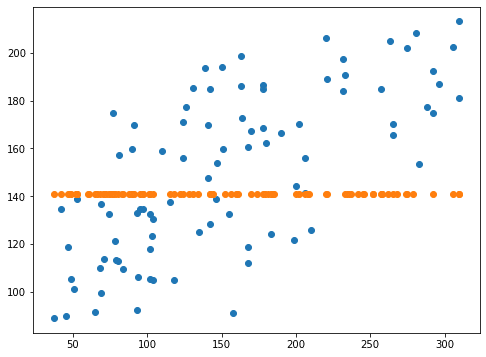
予想値が大きくばらけてきました。
このばらけ具合が広がったことにより、全体的に予想値が正解値に近くなったものだと推測されます。
ということはcoef0は大きければ大きい方がいいのでしょうか?
予想値は一点に収束してしまいました。
これだけ予想値が収束してしまったら、スコアも悪くなるのは当然ですね。
それではcoef0をさらに大きくしてみて100を試してみることにします。
<セル5 coef=100>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=100)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
-0.04093699576058698 -0.024080656168613622スコアはやはり予測が全くできていないという結果になりました。
<セル6 coef=100>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果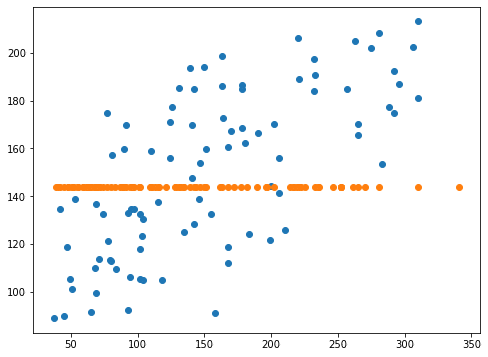
先ほどのcoef0=10と比べてみるとそれほどばらつき具合が変わったようには見えません。
ただこの結果には現れてこない部分である計算時間に差はありました。
coef0=100とすると明らかにcoef=10よりも計算時間が伸びていることから、coef0の値を大きくするに従って計算コストが増大してくようです。
となると計算時間と予想精度のバランスを見極めてcoef0の値を決めていくということが必要そうです。
さてcoef0=10でそこそこ予想精度のスコアが上がったのですが、負の値にしても同じような結果になるのでしょうか。
先ほどのcoef0=10と同じく一点に収束してしまい、予測が全くできていない結果となりました。
それでは負の値はどうでしょうか?
coef0=-10を試してみまることにします。
<セル5 coef0=-10>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=-10)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
-0.050146410763622196 -0.0260889606747322<セル6 coef=-10>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果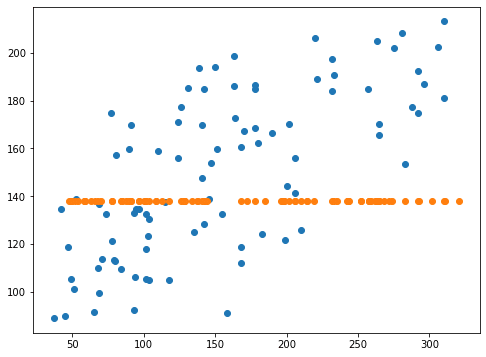
coef0=-10とするとスコアからもグラフからも予想精度が劇的に低下したことが分かります。
coef0=-10としてもやはり一点に収束してしまいました。
となると最初の方に試した1程度のところがいいのでしょうか?
まずは1に近づけるという意味で、coef0=2としてみます。
<セル7 coef0=2>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=2)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
0.1565169463619306 0.16680546010907968<セル8 coef0=2>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果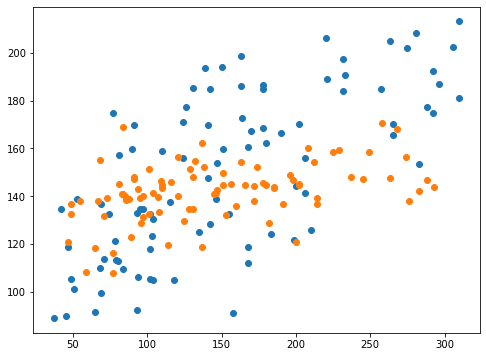
スコア的にもグラフ的にも収束が始まっていて、予想値がずれてきているところが捉えられました。
となると気になるのは、1より小さく0に近いところではどうなるかということです。
<セル9 coef0=0.1>
trial = 100
pred_svr_score = []; pred_svr_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_svr = SVR(kernel="sigmoid", coef0=0.1)
model_svr.fit(x_train, y_train)
pred_svr = model_svr.predict(x_test)
pred_svr_score.append(r2_score(y_test, pred_svr))
pred_svr_train = model_svr.predict(x_train)
pred_svr_train_score.append(r2_score(y_train, pred_svr_train))
pred_svr_ave = np.average(np.array(pred_svr_score))
pred_svr_train_ave = np.average(np.array(pred_svr_train_score))
print(pred_svr_ave, pred_svr_train_ave)
実行結果
0.39739700808925105 0.4092308314055195<セル10 coef0=0.1>
fig=plt.figure(figsize=(8,6))
plt.clf()
plt.scatter(y_test_ori, pred_svr_ori)
plt.scatter(y_test, pred_svr)
実行結果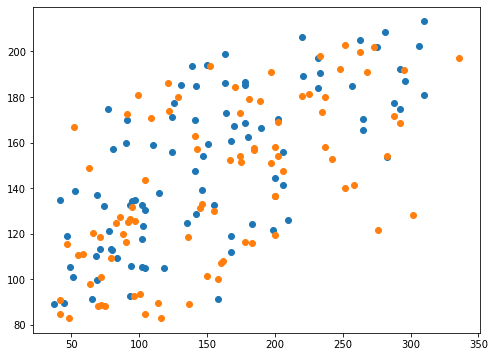
今度はcoef0を指定しない場合とあまり変わらない結果となりました。
こうみると1近くで使って、全体的に予想値を収束させて使うものなのかなという印象を受けました。
裏には色々な計算があるのでしょうが、なかなかそこまで踏み込めないので、ある程度こう言った傾向だけになってしまうのですが、それでも少しパラメータを変えるだけで劇的に変化があると楽しいものです。
それでは次回は最後に残った”poly”に関連するパラメータをいじっていきたいと思います。
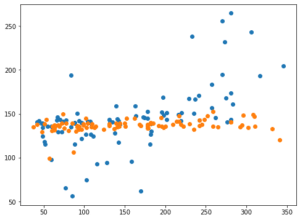
ということで今回はこんな感じで。

コメント
コメント一覧 (2件)
>ということで次はcoef0=10を試してみます。
のトライで結果が良くなっていますが、kernel=”poly”だからではないでしょうか?
coef0=100の場合も”poly”になっています。
road2myhomeさん、ありがとうございます。
仰る通り、”poly”になっていました。”sigmoid”にしてやり直したところ、全く違う結果になって驚いています。
ご指摘ありがとうございましたm(_ _)m