機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnの糖尿病患者のデータセットでSVRモデルを使い、特徴量の全ての組み合わせを検討してみました。
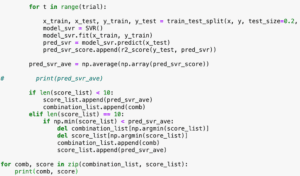
その結果としては、SVRモデルでは「s5」、「bmi」を特徴量として学習させれば十分、だが「bp」、「s4」、「s3」もあっても悪くないという感じでした。
その時出てきた疑問。
この予想精度スコアの高い特徴量の組み合わせは使う機械学習モデルに依存するものなのか?
つまり機械学習モデルによっては、特徴量の他の組み合わせの方が良い予想精度を出せる、なんてことがあるんじゃないかということ。
ということで今回は、前に試した際にスコアの良かったRidgeRegressionモデルを使って特徴量の組み合わせを検討してみたいと思います。
ということでデータの読み込みから。
<セル1>
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df["target"] = diabetes.target
df
実行結果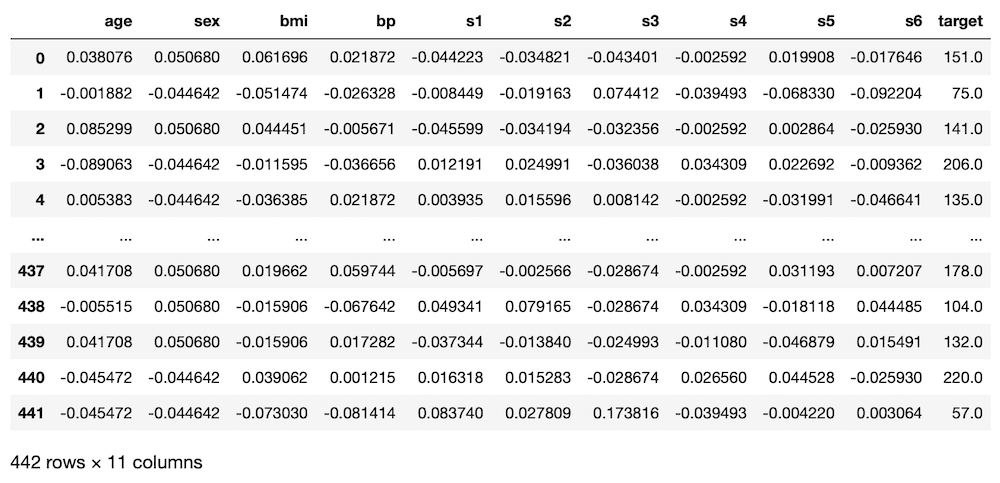
使用する学習モデルをRidgeRegressionモデルに変更する
データの読み込みが終わったところで、プログラムを書き換え、使用する学習モデルをRidgeRegressionモデルに変更していきましょう。
まずはライブラリのインポートから。
前回はこんな感じでした。
import itertools
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np今回はSVRモデルは使わないので「from sklearn.svm import SVR」を削除し、代わりにRidgeRegressionモデルを使うため「from sklearn.linear_model import Ridge」を追加します。
import itertools
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
import numpy as npあとは機械学習モデルの読み込みをSVRからRidgeに書き換えます。
つまりこの部分を
model_svr = SVR()このように書き換えます。
model_rd = Ridge()あとは機械学習モデルを変更したので、変数名も変更しておくと分かりやすいと思います。
私は変数名の「model_svr」とか「pred_svr」、リスト名の「pred_svr_score」などを「model_rd」、「pred_rd」、「pred_rd_score」といった感じに変更しました。
変更したプログラムがこちら。
<セル2>
import itertools
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
import numpy as np
trial=10
score_list = []; combination_list = []
for i in range(1, len(diabetes.feature_names)+1):
print(i)
for comb in itertools.combinations(diabetes.feature_names, i):
# print(comb)
x = df.loc[:, comb]
y = df.loc[:, "target"]
# print(x)
pred_rd_score = []
for t in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model_rd = Ridge()
model_rd.fit(x_train, y_train)
pred_rd = model_rd.predict(x_test)
pred_rd_score.append(r2_score(y_test, pred_rd))
pred_rd_ave = np.average(np.array(pred_rd_score))
# print(pred_rd_ave)
if len(score_list) < 10:
score_list.append(pred_rd_ave)
combination_list.append(comb)
elif len(score_list) == 10:
if np.min(score_list) < pred_rd_ave:
del combination_list[np.argmin(score_list)]
del score_list[np.argmin(score_list)]
combination_list.append(comb)
score_list.append(pred_rd_ave)
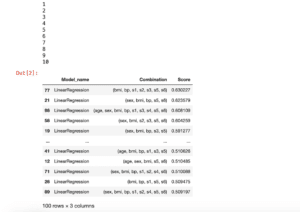
for comb, score in zip(combination_list, score_list):
print(comb, score)
実行結果
('sex', 'bmi', 'bp', 's3', 's4', 's5') 0.439693010132639
('bmi', 'bp', 's1', 's3', 's5', 's6') 0.42800410791192245
('age', 'bmi', 'bp', 's3', 's4', 's5', 's6') 0.4260323203866879
('sex', 'bmi', 'bp', 's1', 's2', 's3', 's5') 0.43784734895660027
('sex', 'bmi', 'bp', 's1', 's3', 's4', 's5') 0.4291064870545248
('sex', 'bmi', 'bp', 's1', 's3', 's5', 's6') 0.43488580704318186
('bmi', 'bp', 's1', 's2', 's3', 's5', 's6') 0.4280862604485365
('age', 'sex', 'bmi', 'bp', 's2', 's3', 's5', 's6') 0.4349084526454246
('age', 'sex', 'bmi', 'bp', 's1', 's2', 's4', 's5', 's6') 0.4264502561900601
('age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6') 0.430405347137590041回実行してみただけですが、もうSVRモデルとは違うなという感じがします。
ということで試していきましょう。
プログラムを5回試してみた
1回目の実行結果
| 特徴量 | スコア | 順位 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’ | 0.43969 | 1 |
| ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’, ‘s6’ | 0.42800 | 8 |
| ‘age’, ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42603 | 10 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s5’ | 0.43785 | 2 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s4’, ‘s5’ | 0.42911 | 6 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’, ‘s6’ | 0.43489 | 4 |
| ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.42809 | 7 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.43491 | 3 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s4’, ‘s5’, ‘s6’ | 0.42645 | 9 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.43041 | 5 |
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 4 | 7 | 10 | 10 | 7 | 5 | 9 | 5 | 10 | 7 |
第一位:’sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’
2回目の実行結果
| 特徴量 | スコア | 順位 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s5’ | 0.42723 | 8 |
| ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’ | 0.42675 | 9 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’ | 0.43032 | 6 |
| ‘age’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s4’, ‘s5’ | 0.43279 | 4 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s4’, ‘s5’ | 0.43033 | 5 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s4’, ‘s5’, ‘s6’ | 0.44193 | 1 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’ | 0.42960 | 7 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.43482 | 3 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.43588 | 2 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42569 | 10 |
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 4 | 8 | 10 | 10 | 7 | 4 | 9 | 5 | 10 | 4 |
第一位:’age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s4’, ‘s5’, ‘s6’
3回目の実行結果
| 特徴量 | スコア | 順位 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s5’ | 0.42208 | 10 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s5’, ‘s6’ | 0.42330 | 9 |
| ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’ | 0.43228 | 5 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s5’, ‘s6’ | 0.42665 | 8 |
| ‘age’, ‘bmi’, ‘bp’, ‘s2’, ‘s4’, ‘s5’, ‘s6’ | 0.43251 | 4 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’, ‘s6’ | 0.43826 | 1 |
| ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42990 | 7 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.43420 | 3 |
| ‘age’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s5’, ‘s6’ | 0.43605 | 2 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.43166 | 6 |
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 4 | 6 | 10 | 10 | 3 | 7 | 9 | 4 | 10 | 8 |
第一位:’sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’, ‘s6’
4回目の実行結果
| 特徴量 | スコア | 順位 |
| ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’ | 0.42768 | 10 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s5’ | 0.43514 | 3 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’ | 0.43426 | 4 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s4’, ‘s5’ | 0.42954 | 5 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s4’, ‘s5’, ‘s6’ | 0.42890 | 7 |
| ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42914 | 6 |
| ‘age’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’ | 0.42829 | 9 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.43902 | 2 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42835 | 8 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.46455 | 1 |
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 3 | 7 | 10 | 10 | 4 | 7 | 9 | 9 | 10 | 5 |
第一位:’age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’
5回目の実行結果
| 特徴量 | スコア | 順位 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s4’, ‘s5’ | 0.42470 | 9 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s5’, ‘s6’ | 0.42902 | 6 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s5’, ‘s6’ | 0.43284 | 3 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s3’, ‘s5’, ‘s6’ | 0.42783 | 7 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42465 | 10 |
| ‘age’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.43088 | 4 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’ | 0.43025 | 5 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.44926 | 1 |
| ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.44691 | 2 |
| ‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’ | 0.42657 | 8 |
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 4 | 9 | 10 | 10 | 4 | 6 | 9 | 7 | 10 | 8 |
第一位:’age’, ‘sex’, ‘bmi’, ‘bp’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’
各特徴量の出現回数まとめ
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
| 19 | 37 | 50 | 50 | 25 | 29 | 45 | 30 | 50 | 32 |
RidgeRegressionモデルではSVRモデルと比べて、予想精度のスコアが高いものには特徴量の数が多い傾向がありました。
しかしながら全ての特徴量を使った方がスコアが高いかというとそうではないようです。
またSVRモデルで重要だった「bmi」、「s5」、「bp」は全ての組み合わせに含まれていますが、その3つの組み合わせだけというのは今回の結果には一度も出てきませんでした。
このことから予想するにRidgeRegressionモデルとSVRモデルではその機械学習の方向性が異なっており、それが今回の予想精度スコアの高い特徴量の組み合わせの違いとして表れたと考えられます。
つまり最初の問いである「この予想精度スコアの高い特徴量の組み合わせは使う機械学習モデルに依存するものなのか?」の答えは「依存する」ということになります。
となると一番良い機械学習モデル、特徴量の組み合わせを今回のように計算から導き出すというのも一つの方針としてありなのではないでしょうか。
ということで次回はこの全部の特徴量の組み合わせを試すプログラムを複数のモデルに対して自動で計算できるよう改変していきたいと思います。
ではでは今回はこんな感じで。

コメント