機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnで複数の機械学習モデルで特徴量全ての組み合わせを試すためのプログラムを作成しました。
今回はそのプログラムを使って、どんな結果が出るのか試してみたいと思います。
ということで前回のプログラムのおさらいから。
まずはデータの読み込みから。
<セル1>
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df["target"] = diabetes.target
df
実行結果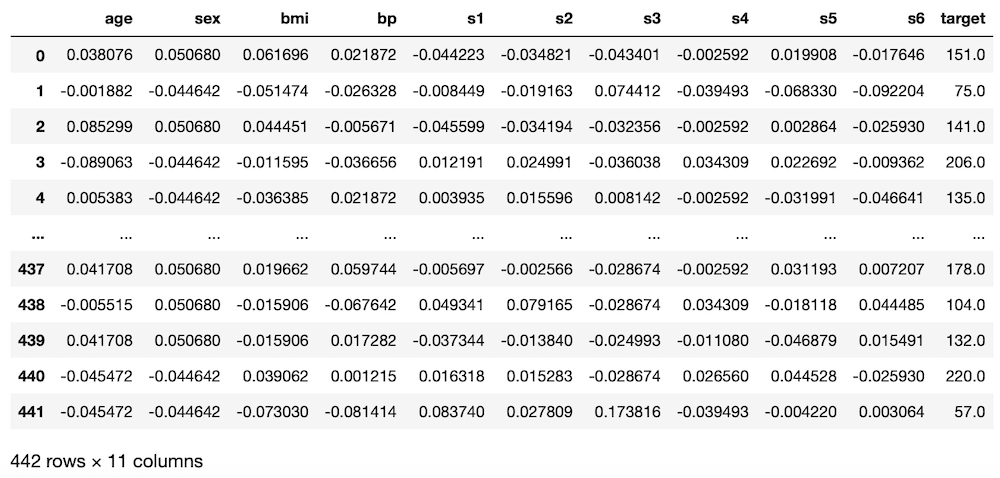
次に機械学習から評価、表示までのプログラム。
ちなみに前回とtrial数を変えて10回にしておきます「trial=10」。
また最後の行の結果を表示する「results」ですが、とりあえずTOP10のみ表示させるよう「results.head(10)」としておきます。
<セル2>
import itertools
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np
models = ["LinearRegression", "Lasso", "ElasticNet", "RidgeRegression", "SVR"]
trial=10
score_list = []; combination_list = []; model_list = []
for i in range(1, len(diabetes.feature_names)+1):
print(i)
for comb in itertools.combinations(diabetes.feature_names, i):
# print(comb)
x = df.loc[:, comb]
y = df.loc[:, "target"]
# print(x)
for mod in models:
pred_score = []
for t in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
if mod == "LinearRegression":
model = LinearRegression()
elif mod == "Lasso":
model = Lasso()
elif mod == "ElasticNet":
model = ElasticNet()
elif mod == "RidgeRegression":
model = Ridge()
elif mod == "SVR":
model = SVR()
model.fit(x_train, y_train)
pred = model.predict(x_test)
pred_score.append(r2_score(y_test, pred))
# print(mod, r2_score(y_test, pred))
pred_ave = np.average(np.array(pred_score))
# print(pred_ave)
if len(score_list) < 100:
score_list.append(pred_ave)
combination_list.append(comb)
model_list.append(mod)
elif len(score_list) == 100:
if np.min(score_list) < pred_ave:
del combination_list[np.argmin(score_list)]
del model_list[np.argmin(score_list)]
del score_list[np.argmin(score_list)]
combination_list.append(comb)
score_list.append(pred_ave)
model_list.append(mod)
results = pd.DataFrame()
results["Model_name"] = model_list
results["Combination"] = combination_list
results["Score"] = score_list
results = results.sort_values("Score", ascending=False)
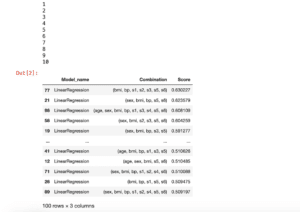
results.head(10)
実行結果
とりあえず5回試してみる
ということで早速5回ほど実行してみて、どういう結果になるのか見てみましょう。
1回目
| 順位 | 学習モデル | 組み合わせ | スコア |
| 1 | LinearRegression | (sex, bmi, bp, s1, s2, s3, s4, s5) | 0.539114 |
| 2 | LinearRegression | (sex, bmi, bp, s2, s4, s5) | 0.535420 |
| 3 | LinearRegression | (sex, bmi, bp, s1, s2, s3, s5) | 0.527867 |
| 4 | LinearRegression | (sex, bmi, s2, s3, s5) | 0.518247 |
| 5 | LinearRegression | (age, sex, bmi, bp, s2, s4, s5) | 0.516298 |
| 6 | LinearRegression | (sex, bmi, s1, s2, s3, s4, s5, s6) | 0.514418 |
| 7 | LinearRegression | (sex, bmi, bp, s1, s2, s3, s5, s6) | 0.514041 |
| 8 | LinearRegression | (age, sex, bmi, bp, s2, s3, s5, s6) | 0.511945 |
| 9 | LinearRegression | (bmi, bp, s3, s4, s5) | 0.510244 |
| 10 | LinearRegression | (age, sex, bmi, bp, s2, s3, s4, s5) | 0.508619 |
2回目
| 順位 | 学習モデル | 組み合わせ | スコア |
| 1 | LinearRegression | (age, sex, bmi, bp, s2, s5) | 0.532929 |
| 2 | LinearRegression | (age, sex, bmi, bp, s3, s4, s5, s6) | 0.531614 |
| 3 | LinearRegression | (sex, bmi, s2, s3, s5, s6) | 0.529759 |
| 4 | LinearRegression | (age, sex, bmi, bp, s1, s2, s3, s5) | 0.518262 |
| 5 | LinearRegression | (age, bmi, bp, s1, s4, s5) | 0.517232 |
| 6 | RidgeRegression | (sex, bmi, s3, s5) | 0.515282 |
| 7 | LinearRegression | (sex, bmi, bp, s3, s4, s5, s6) | 0.514030 |
| 8 | RidgeRegression | (bmi, bp, s3, s5) | 0.511027 |
| 9 | LinearRegression | (age, bmi, bp, s1, s2, s3, s5, s6) | 0.508957 |
| 10 | LinearRegression | (sex, bmi, bp, s2, s4, s5, s6) | 0.508051 |
3回目
| 順位 | 学習モデル | 組み合わせ | スコア |
| 1 | LinearRegression | (sex, bmi, bp, s1, s3, s5) | 0.523996 |
| 2 | LinearRegression | (sex, bmi, bp, s2, s3, s4, s5) | 0.519729 |
| 3 | LinearRegression | (age, sex, bmi, bp, s2, s4, s5, s6) | 0.519441 |
| 4 | LinearRegression | (age, sex, bmi, bp, s3, s4, s5) | 0.517380 |
| 5 | LinearRegression | (sex, bmi, bp, s3, s5, s6) | 0.516548 |
| 6 | LinearRegression | (age, sex, bmi, bp, s1, s2, s4, s5, s6) | 0.515647 |
| 7 | LinearRegression | (sex, bmi, bp, s2, s5) | 0.515263 |
| 8 | LinearRegression | (sex, bmi, bp, s2, s3, s5) | 0.514185 |
| 9 | LinearRegression | (sex, bmi, bp, s2, s5, s6) | 0.513732 |
| 10 | LinearRegression | (sex, bmi, bp, s1, s2, s4, s5, s6) | 0.509704 |
4回目
| 順位 | 学習モデル | 組み合わせ | スコア |
| 1 | LinearRegression | (sex, bmi, bp, s3, s5) | 0.543179 |
| 2 | LinearRegression | (sex, bmi, bp, s1, s4, s5) | 0.525615 |
| 3 | LinearRegression | (sex, bmi, bp, s1, s5, s6) | 0.525553 |
| 4 | LinearRegression | (sex, bmi, bp, s1, s3, s4, s5, s6) | 0.525465 |
| 5 | LinearRegression | (sex, bmi, bp, s3, s4, s5) | 0.525174 |
| 6 | LinearRegression | (sex, bmi, bp, s1, s2, s5) | 0.520274 |
| 7 | LinearRegression | (sex, bmi, bp, s5, s6) | 0.516243 |
| 8 | LinearRegression | (age, sex, bmi, bp, s1, s4, s5) | 0.514241 |
| 9 | LinearRegression | (sex, bmi, bp, s2, s3, s4, s5, s6) | 0.514057 |
| 10 | LinearRegression | (age, sex, bmi, bp, s3, s5, s6) | 0.512873 |
5回目
| 順位 | 学習モデル | 組み合わせ | スコア |
| 1 | LinearRegression | (age, sex, bmi, bp, s3, s5, s6) | 0.524668 |
| 2 | LinearRegression | (bmi, bp, s1, s2, s5) | 0.520597 |
| 3 | LinearRegression | (sex, bmi, bp, s3, s5) | 0.520161 |
| 4 | LinearRegression | (sex, bmi, bp, s1, s5) | 0.520110 |
| 5 | LinearRegression | (age, sex, bmi, bp, s3, s5) | 0.515293 |
| 6 | LinearRegression | (age, bmi, s2, s3, s4, s5, s6) | 0.513540 |
| 7 | LinearRegression | (age, sex, bmi, bp, s2, s4, s5, s6) | 0.513027 |
| 8 | LinearRegression | (sex, bmi, bp, s2, s5) | 0.511537 |
| 9 | LinearRegression | (age, sex, bmi, bp, s1, s2, s5, s6) | 0.510046 |
| 10 | LinearRegression | (bmi, bp, s2, s4, s5, s6) | 0.508750 |
考察してみる
驚いたのは上位のほとんどがLinearRegressionで占められてしまったことです。
前にやった検討ではLinearRegressionモデルの予想精度のスコアは0.45程度。
そしてRidgeRegressionモデルも同じくらいの予想精度があったはず。
それと比べると今回のLinearRegressionモデルの予想精度のスコアは0.5を超えており、前と比べると良すぎるスコアになっています。
このことから今回のデータというのは、これまでと何かがちょっと違うのではないかと考えられます。
それでは一体何が違うのか?
今回変えたところは特徴量において全ての組み合わせを試すようにしたこと。
またtrial数、つまりは平均値を算出するための試行回数を100回から10回に変更したことです。
ここで一度試している組み合わせ数に関して計算してみましょう。
特徴量10個のものに対して、全ての組み合わせを計算すると、
10C1 + 10C2 + 10C3 + 10C4 + 10C5 + 10C6 + 10C7 + 10C8 + 10C9 + 10C10
つまり 10 + 45 + 120 + 210 + 252 + 210 + 120 + 45 + 10 + 1 = 1023通り となります。
特に10の特徴量から4つ(10C4)、5つ(10C5)、6つ(10C6)取り出す時の組み合わせは他のものよりも倍程度多くなっています。
ただこれはどの機械学習モデルでも同じことであり、LinearRegressionモデルだけに限ったことではありません。
もう一つの試行回数を100回から10回に減らしたことはどうでしょう。
もし出てくるスコアのばらつきが大きく、例えば0.7のものもあれば、0.3のものもある場合、試行回数が十分あれば平均値である0.5が取得できることでしょう。
ですが試行回数が少ない場合、例えば0.7、0.6、0.7、0.5、0.6のように高い数値に偏ってしまう可能性が考えられます。
とりあえずLinearRegressionモデルでこのようにスコアが大きくばらついているのか確認してみましょう。
LinearRegressionモデルのスコアのばらつきを確認してみる
それではLinearRegressionモデルでのばらつきを確認していきましょう。
今回は特徴量を全て使い、100回学習と評価を繰り返したのち、平均値、最大値、最小値、標準偏差を計算するプログラムを書いてみます。
<セル3>
x = df.loc[:, ["age", "sex", "bmi", "bp", "s1", "s2", "s3", "s4", "s5", "s6"]]
y = df.loc[:, "target"]
trial = 100
pred_score = []; pred_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
pred_score.append(r2_score(y_test, pred))
pred_ave = np.average(np.array(pred_score))
pred_max = np.max(np.array(pred_score))
pred_min = np.min(np.array(pred_score))
pred_std = np.std(np.array(pred_score))
print(pred_ave, pred_max, pred_min, pred_std)
実行結果
0.4814766954911379 0.620899838132245 0.25614892681740276 0.0664189148607429これを10回試行のものを5回、100回試行のものを5回やって値がどうばらつくのか見てみましょう。
10回試行
| 平均値 | 最大値 | 最小値 | 標準偏差 | |
| 1回目 | 0.45590 | 0.55582 | 0.31871 | 0.06414 |
| 2回目 | 0.48846 | 0.61605 | 0.33118 | 0.09195 |
| 3回目 | 0.47151 | 0.54177 | 0.33753 | 0.05600 |
| 4回目 | 0.49178 | 0.55555 | 0.41555 | 0.04115 |
| 5回目 | 0.47520 | 0.57379 | 0.39472 | 0.05111 |
100回試行
| 平均値 | 最大値 | 最小値 | 標準偏差 | |
| 1回目 | 0.48162 | 0.64570 | 0.28003 | 0.07372 |
| 2回目 | 0.47859 | 0.61281 | 0.20102 | 0.07484 |
| 3回目 | 0.48937 | 0.61791 | 0.31921 | 0.06646 |
| 4回目 | 0.48238 | 0.62020 | 0.25591 | 0.07737 |
| 5回目 | 0.46935 | 0.68781 | 0.28080 | 0.07099 |
平均値の最大値と最小値の差分としては10回試行で0.03278(0.49178-0.45590)、100回試行で0.02002(0.48937-0.46935)ということで確かに100回試行の方が平均値のばらつきは小さくなっています。
ただしそれぞれの試行回で見てみると最大値、最小値の開きは10回試行のときよりも100回試行の方が大きくなっています。
試行回数が増えるにしたがって、外れた値が出やすくなってしまうので、これは仕方のないことかもしれません。
このことから100回試行の方がやはりスコアの平均値は収束しやすく、外れた値になりにくいと考えられます。
かと言って、このプログラムは先ほど計算した通り、1つのモデルに対し1023通りの組み合わせを計算します。
そして試行回数が10回であれば、10230回の機械学習・予想・評価を行うわけです。
100回にするとその10倍、残念ながらMacBook “Air”を使っている私の環境では計算に時間がかかり過ぎてしまいます。
ちなみにRidgeRegressionモデルではどうなのでしょうか?
RidgeRegressionモデルのスコアのばらつきを確認してみる
ということで試してみましょう。
<セル4>
x = df.loc[:, ["age", "sex", "bmi", "bp", "s1", "s2", "s3", "s4", "s5", "s6"]]
y = df.loc[:, "target"]
trial = 10
pred_score = []; pred_train_score = []
for i in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
model = Ridge()
model.fit(x_train, y_train)
pred = model.predict(x_test)
pred_score.append(r2_score(y_test, pred))
pred_ave = np.average(np.array(pred_score))
pred_max = np.max(np.array(pred_score))
pred_min = np.min(np.array(pred_score))
pred_std = np.std(np.array(pred_score))
print(pred_ave, pred_max, pred_min, pred_std)
実行結果
0.4146294707871937 0.44320724340491413 0.3438771552368486 0.02616811676869301先ほどと同じように10回試行と100回試行を試してみましょう。
10回試行
| 平均値 | 最大値 | 最小値 | 標準偏差 | |
| 1回目 | 0.41463 | 0.44321 | 0.34388 | 0.02617 |
| 2回目 | 0.40453 | 0.45832 | 0.32691 | 0.04727 |
| 3回目 | 0.41834 | 0.51132 | 0.32546 | 0.05051 |
| 4回目 | 0.42851 | 0.50359 | 0.30177 | 0.05637 |
| 5回目 | 0.39887 | 0.46098 | 0.26662 | 0.06562 |
100回試行
| 平均値 | 最大値 | 最小値 | 標準偏差 | |
| 1回目 | 0.41897 | 0.52164 | 0.25301 | 0.04551 |
| 2回目 | 0.41505 | 0.51317 | 0.30915 | 0.04322 |
| 3回目 | 0.41506 | 0.50304 | 0.27034 | 0.04213 |
| 4回目 | 0.41287 | 0.52216 | 0.28756 | 0.04211 |
| 5回目 | 0.40806 | 0.51493 | 0.28608 | 0.04714 |
まず平均値の最大値と最小値の差分を見ていくと、10回試行では0.02964(0.42851-0.39887)、100回試行では0.01091(0.41897-0.40806)。
先ほどのLinearRegressionより低い値となり、RidgeRegressionモデルの方が安定した結果が出やすいと考えられます。
またそれぞれの試行回の標準偏差を見ても、LinearRegressionモデルよりもRidgeRegressionモデルの方が小さくなっており、やはりRidgeRegressionモデルの方が安定した結果が得られやすいという結果になりました。
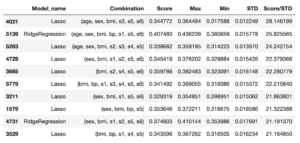
となるとそれぞれのモデルの評価を行うには、この安定性という指標も入れないと、フェアにならないのではないかと考えられます。
ということで次回はさらにプログラムを改変し、より精度のいい機械学習モデルと特徴量の組み合わせを得られるようにしたいと思います。
ではでは今回はこんな感じで。

コメント