機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnで複数の機械学習モデルで特徴量全ての組み合わせを試すためのプログラムに円グラフで表示する機能を追加しました。

今回はそのプログラムを使って、新しい指標を使い、複数の機械学習モデルで特徴量全ての組み合わせを試した場合、使われやすい機械学習モデルはどれなのか、検討してみたいと思います。
ということでおさらいから。
<セル1>
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df["target"] = diabetes.target
df
実行結果
<セル2>
import itertools
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.metrics import r2_score
import numpy as np
models = ["LinearRegression", "Lasso", "ElasticNet", "RidgeRegression", "SVR"]
trial=10
score_list = []; combination_list = []; model_list = []
std_list = []; max_list = []; min_list = []; score_std_list = []
for i in range(1, len(diabetes.feature_names)+1):
print(i)
for comb in itertools.combinations(diabetes.feature_names, i):
# print(comb)
x = df.loc[:, comb]
y = df.loc[:, "target"]
# print(x)
for mod in models:
pred_score = []
for t in range(trial):
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, train_size=0.8)
if mod == "LinearRegression":
model = LinearRegression()
elif mod == "Lasso":
model = Lasso()
elif mod == "ElasticNet":
model = ElasticNet()
elif mod == "RidgeRegression":
model = Ridge()
elif mod == "SVR":
model = SVR()
model.fit(x_train, y_train)
pred = model.predict(x_test)
pred_score.append(r2_score(y_test, pred))
# print(mod, r2_score(y_test, pred))
combination_list.append(comb)
score_list.append(np.average(np.array(pred_score)))
std_list.append(np.std(np.array(pred_score)))
max_list.append(np.max(np.array(pred_score)))
min_list.append(np.min(np.array(pred_score)))
model_list.append(mod)
results = pd.DataFrame()
results["Model_name"] = model_list
results["Combination"] = combination_list
results["Score"] = score_list
results["Max"] = max_list
results["Min"] = min_list
results["STD"] = std_list
results["Score/STD"] = results["Score"]/results["STD"]
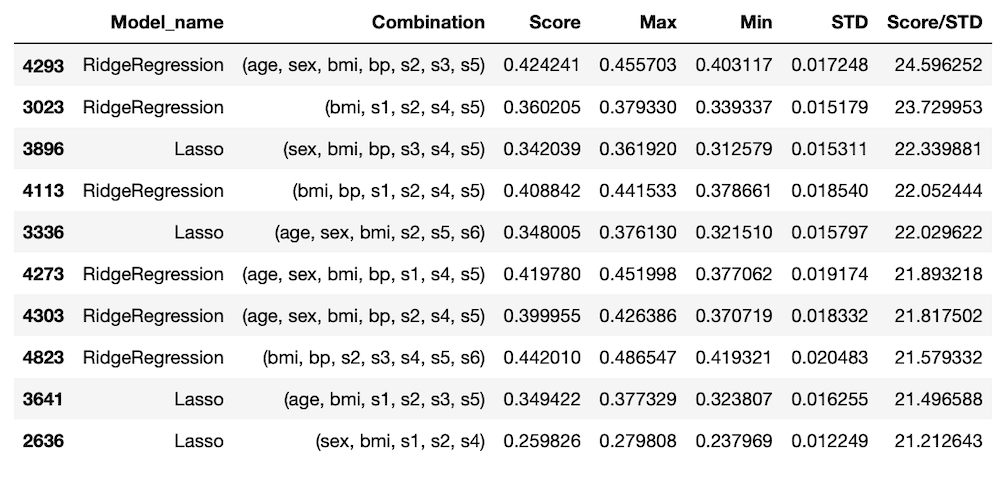
results = results.sort_values("Score/STD", ascending=False)
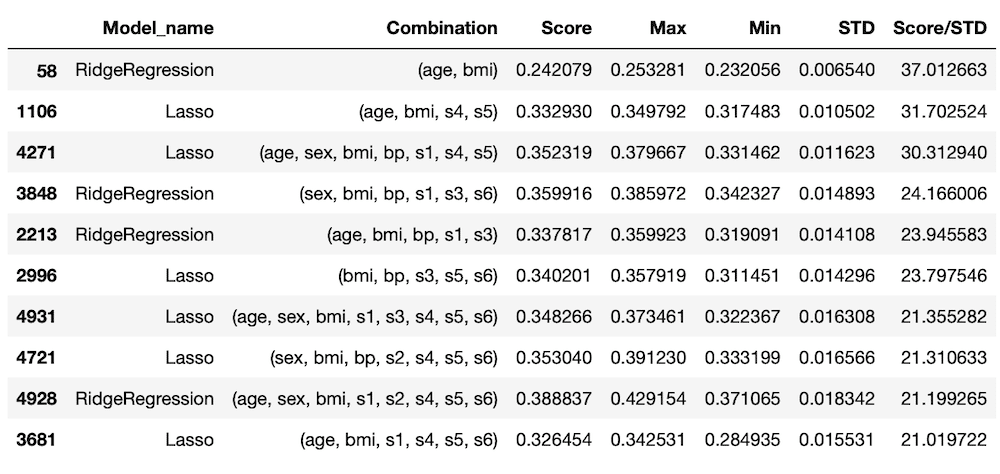
results.head(10)
実行結果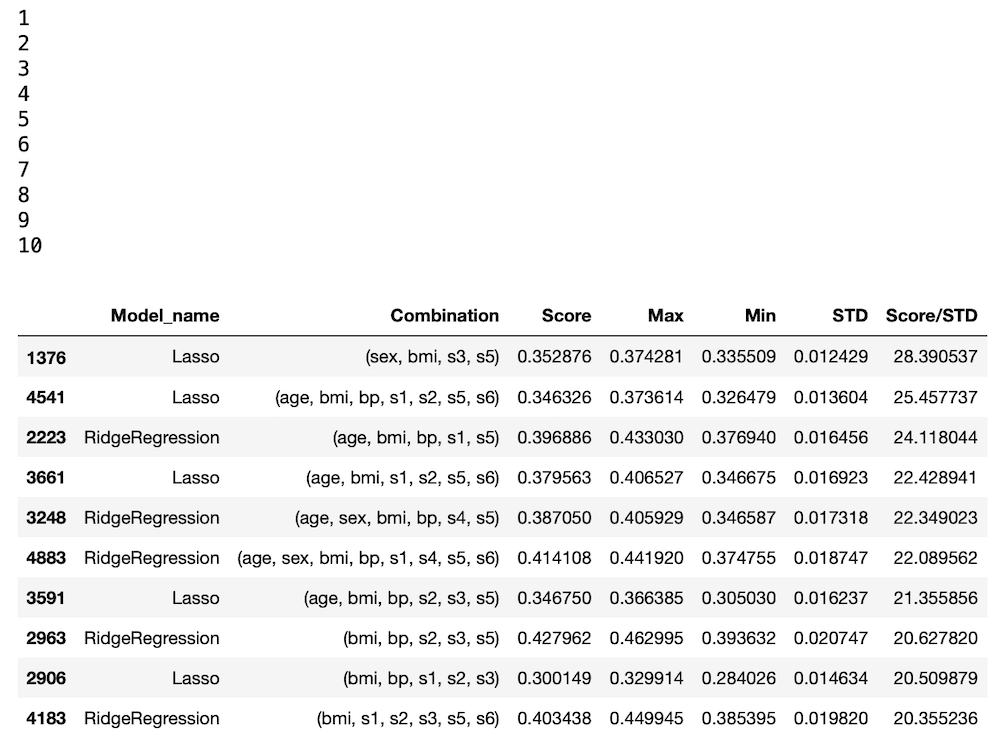
<セル3>
ranking = 100
lr_count = results["Model_name"][:ranking][results["Model_name"] == "LinearRegression"].count()
lasso_count = results["Model_name"][:ranking][results["Model_name"] == "Lasso"].count()
en_count = results["Model_name"][:ranking][results["Model_name"] == "ElasticNet"].count()
rd_count = results["Model_name"][:ranking][results["Model_name"] == "RidgeRegression"].count()
svr_count = results["Model_name"][:ranking][results["Model_name"] == "SVR"].count()
model_count_list = [lr_count, lasso_count, en_count, rd_count, svr_count]
print(model_count_list)
実行結果
[8, 46, 0, 44, 2]<セル4>
from matplotlib import pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(8,6))
plt.clf()
plt.pie(model_count_list, labels=models)
実行結果
([<matplotlib.patches.Wedge at 0x7fca3a5a6510>,
<matplotlib.patches.Wedge at 0x7fca3a5a6990>,
<matplotlib.patches.Wedge at 0x7fca3a5a6950>,
<matplotlib.patches.Wedge at 0x7fca3a5b8050>,
<matplotlib.patches.Wedge at 0x7fca3a5b8e90>],
[Text(1.0654414787782402, 0.27355886989611045, 'LinearRegression'),
Text(-0.4049370232742901, 1.0227541284110062, 'Lasso'),
Text(-1.0654414659720242, -0.2735589197730251, 'ElasticNet'),
Text(0.06906960848527893, -1.0978293989430645, 'RidgeRegression'),
Text(1.0978294029847897, -0.06906954424390042, 'SVR')])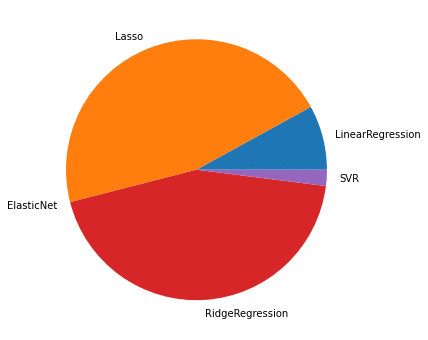
5回実行してみる
今回も5回実行していきますが、出現回数をカウントするのは100位までと1,000位までの2種類を試してみましょう。
1回目
| モデル名 | 100位までの出現回数 | 1,000位までの出現回数 |
| LinearRegression | 10 | 157 |
| Lasso | 51 | 413 |
| ElasticNet | 0 | 0 |
| RidgeRegression | 39 | 395 |
| SVR | 0 | 35 |
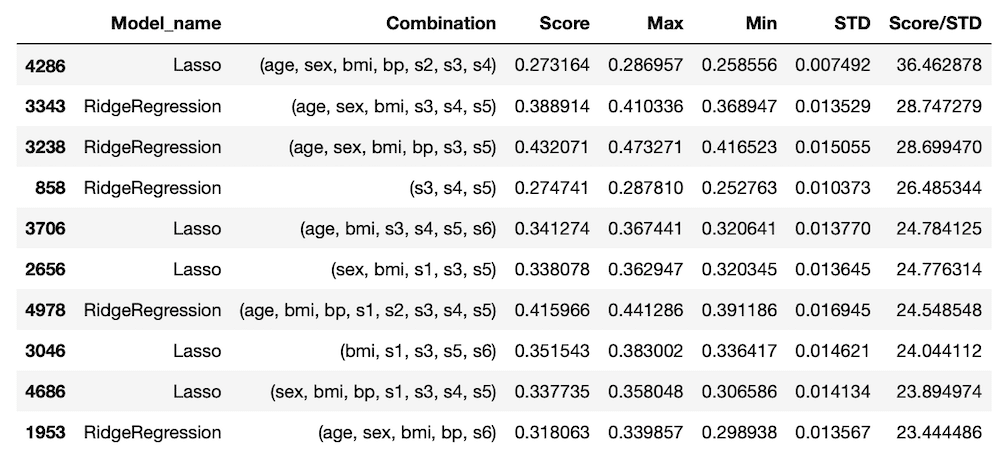
TOP10のデータ
100位までの円グラフ
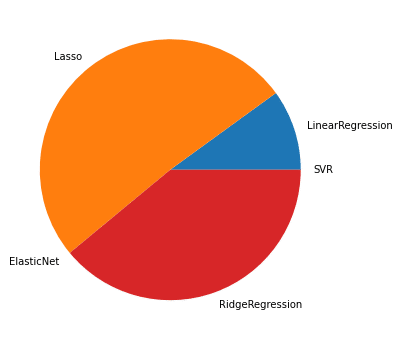
1,000位までの円グラフ
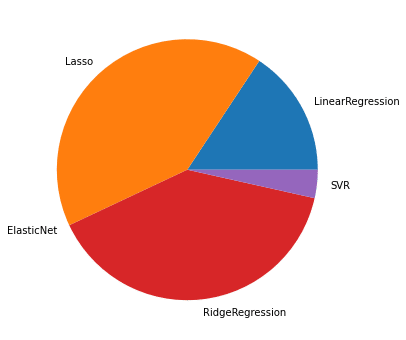
1回目の結果として、多いのは「Lasso」と「RidgeRegression」。
「LinearRegression」と「SVR」は100位まででは出現回数は少ないが、1,000位までになると増加傾向にある。
2回目
| モデル名 | 100位までの出現回数 | 1,000位までの出現回数 |
| LinearRegression | 5 | 165 |
| 0Lasso | 61 | 414 |
| ElasticNet | 0 | 0 |
| RidgeRegression | 34 | 401 |
| SVR | 0 | 20 |
TOP10のデータ
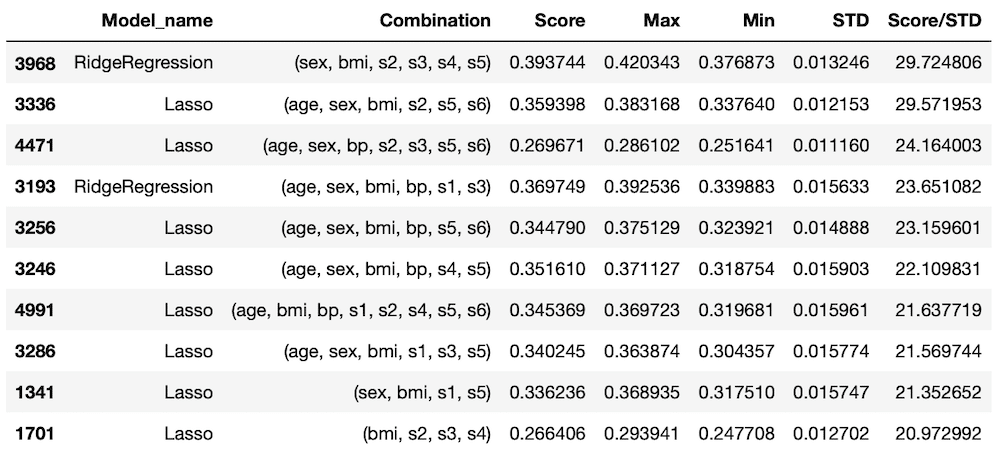
100位までの円グラフ
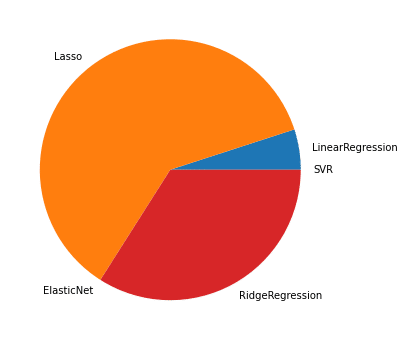
1,000位までの円グラフ
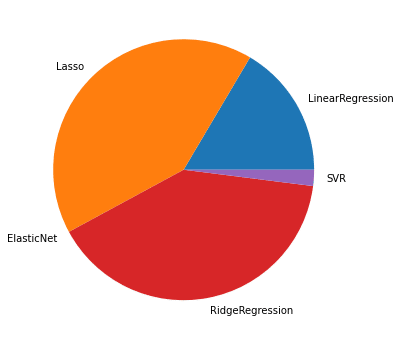
100位までだと1回目よりも「Lasso」の比率が高くなっていますが、1,000位までだと1回目と同じ傾向のグラフになりました。
3回目
| モデル名 | 100位までの出現回数 | 1,000位までの出現回数 |
| LinearRegression | 5 | 137 |
| Lasso | 53 | 432 |
| ElasticNet | 0 | 0 |
| RidgeRegression | 40 | 397 |
| SVR | 2 | 34 |
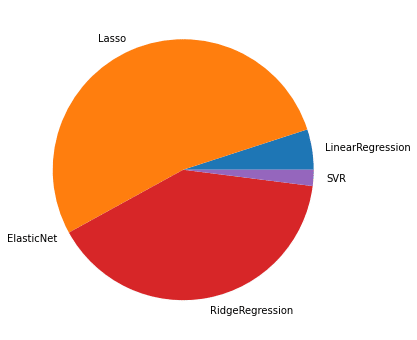
TOP10のデータ
100位までの円グラフ
1,000位までの円グラフ
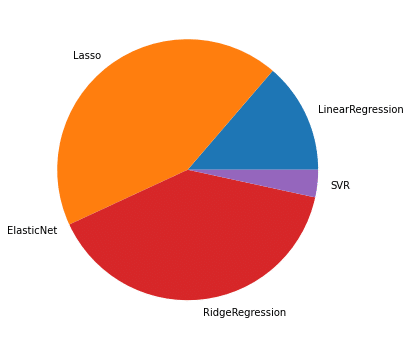
3回目は1回目と傾向は同じで、「Lasso」と「RidgeRegression」が多く、「LinearRegression」と「SVR」は1,000位までに増やすと出現回数が増加しています。
4回目
| モデル名 | 100位までの出現回数 | 1,000位までの出現回数 |
| LinearRegression | 7 | 139 |
| Lasso | 59 | 424 |
| ElasticNet | 0 | 0 |
| RidgeRegression | 34 | 413 |
| SVR | 0 | 24 |
TOP10のデータ
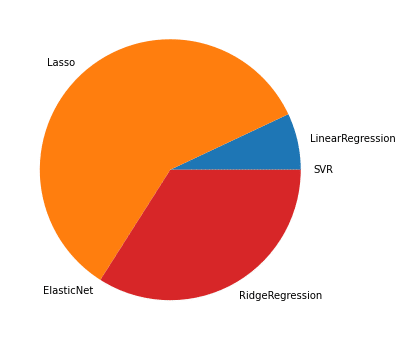
100位までの円グラフ
1,000位までの円グラフ
これも大体傾向は変わらずですね。
5回目
| モデル名 | 100位までの出現回数 | 1,000位までの出現回数 |
| LinearRegression | 3 | 149 |
| Lasso | 50 | 438 |
| ElasticNet | 0 | 0 |
| RidgeRegression | 47 | 379 |
| SVR | 0 | 34 |
TOP10のデータ
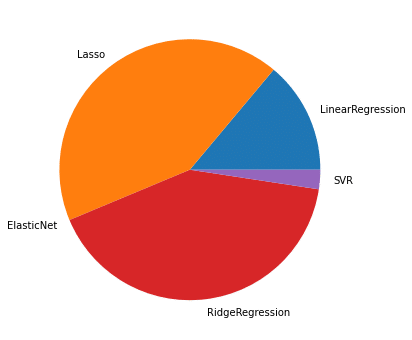
100位までの円グラフ
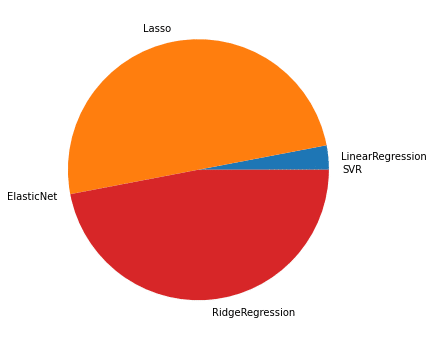
1,000位までの円グラフ
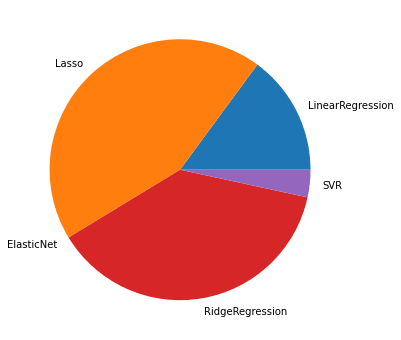
これも傾向は変わらず。
今回の結果としては、「Lasso」か「RidgeRegression」が他の機械学習モデルと比較して選ばれやすいということが分かりました。
しかし本当に「Lasso」と「RidgeRegression」が糖尿病患者のデータセットに対して”良い”機械学習モデルなのでしょうか?
スコアをちゃんと見直してみましょう。
スコアと標準偏差の平均値を比べてみる
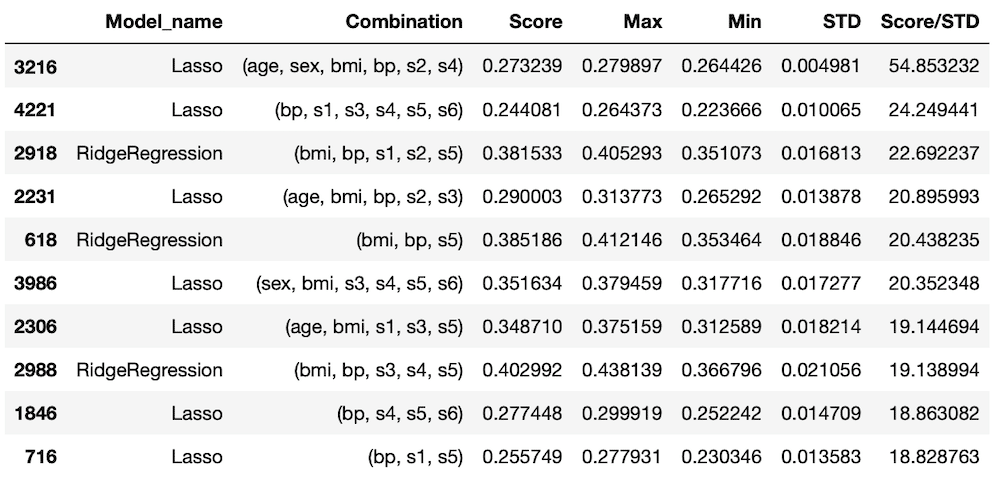
ということで5回目のデータでTOP100以内の「Lasso」と「RidgeRegression」のスコアと標準偏差の平均値を表示させてみましょう。
<セル5>
ranking = 100
lasso_score_ave = results["Score"][:ranking][results["Model_name"] == "Lasso"].mean()
lasso_std_ave = results["STD"][:ranking][results["Model_name"] == "Lasso"].mean()
rd_score_ave = results["Score"][:ranking][results["Model_name"] == "RidgeRegression"].mean()
rd_std_ave = results["STD"][:ranking][results["Model_name"] == "RidgeRegression"].mean()
print(lasso_ave, lasso_std_ave)
print(rd_score_ave, rd_std_ave)
実行結果
0.2920837830657702 0.0183727782298612
0.3654750225200919 0.021773240517050107results[“Score”]で”Score”の列のデータを取得し、[:ranking]で変数rankingの数値までの個数のデータを取得、[results[“Model_name”] == “Lasso”]で”Model_name”が”Lasso” に一致するものを取得し、「.mean()」で平均値を計算しています。
実行結果を見てみるとよく分かります。
ちなみに100位までの出現回数はLassoが50回、RidgeRegressionは47回なので、ここに大きな差はありません。
Lassoの場合は平均スコアが0.29208で、平均標準偏差が0.18373。
RidgeRegressionでは平均スコアが0.36548、平均標準偏差が0.21773。
ということはLassoがスコアの上位を占めているのは、標準偏差が小さいからということになります。
さらに平均スコアと標準偏差の小ささからみると「RidgeRegression」が良いという結論に至ります。
こうなってくるとこのプログラムで上位に入るような特徴量の組み合わせはどういったものなのか気になってきます。
ということで次回、さらにプログラムを追加して、特徴量のカウントをできるようにして検討してみましょう。
ではでは今回はこんな感じで。

コメント