機械学習ライブラリScikit-learn
前回、機械学習ライブラリScikit-learnで複数の機械学習モデルで特徴量全ての組み合わせを試し、RidgeRegressionモデルに対して使われやすい特徴量をグラフ化して分析してみました。
残念ながら前回の検討はいい結果とならなかったのですが、これまで色々試した中で浮かんできた疑問が、特徴量使って計算した値が良い特徴量とならないかということです。
今回はその手始めとして、全ての特徴量を二乗して新たな特徴量として、良い特徴量となりそうか、相関マップをみてみようと思います。
ということで今回はプログラムを一新していきますよ。
データの読み込み
まずはデータの読み込みからですが、これまでと少し変わって、ここではターゲットを読み込みません。
相関マップの一番右の列と一番下の行にターゲットを表示したいため、全ての特徴量をデータフレームに追加した後でターゲットの列を追加します。
ということでこんな感じ。
<セル1>
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df
実行結果
読み込めました。
いつもと違い、一番右の列に「target」はありません。
それぞれの特徴量の二乗を計算し、データフレームに追加
次にそれぞれの特徴量の二乗を計算し、新しい特徴量としてデータフレームに追加していきます。
現在特徴量は10個なので、このまま一つ一つ計算し、データフレームに追加していってもいいのですが、今後さらに特徴量が増える可能性も考え、for文を使って計算、データフレームに追加していきましょう。
<セル2>
for n in diabetes.feature_names:
dataname = n + "^2"
df[dataname] = df[n] * df[n]
df["target"] = diabetes.target
df
実行結果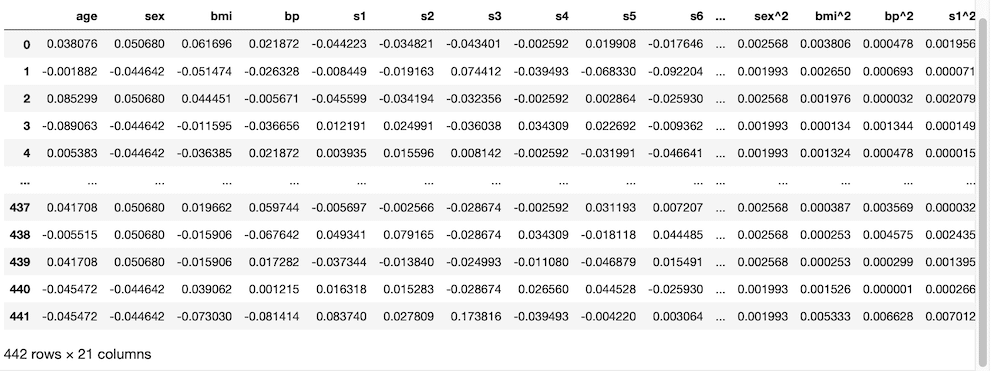
特徴量が多くなりすぎて、途中で省略されてしまっていますが、一番下の「442 rows × 21 columns」から特徴量が2倍(最後の1つはtarget)になっており、処理が正しくできていることが分かります。
最後の「df[“target”] = diabetes.target」はいつも通りターゲットの列を追加しているだけです。
いつもと違うのはこちらの3行。
for n in diabetes.feature_names:
dataname = n + "^2"
df[dataname] = df[n] * df[n]まず「diabetes.featrue_names」はデータベースの特徴量の名前が入っているリストなので、for文を使ってその名前を一つ取得しています。
そして「dataname = n + “^2″」で新しい特徴量の名前を作成しています。
今回は特徴量を二乗するので、新しい特徴量の列として「df[dataname]」を、その中身として「df[n] * df[n]」、つまりnがある一つの特徴量名を取得しているため、ある列を二乗していることになります。
相関値の計算
次にそれぞれの相関値の計算を行います。
これはこちらの記事でも紹介している通り「corr = df.corr()」の1行でできます。
<セル3>
corr = df.corr()
corr
実行結果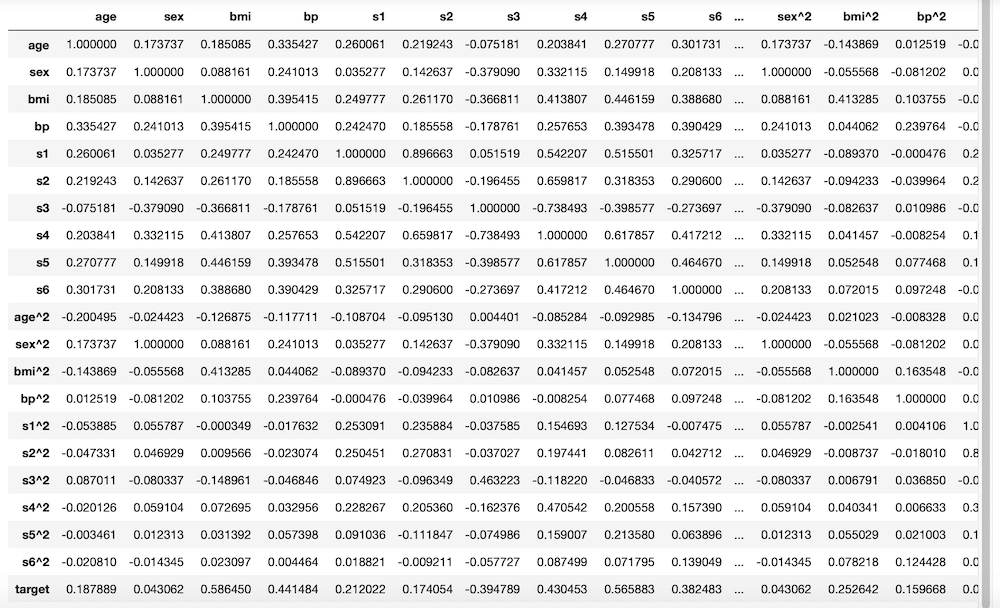
図の一番下が切れてしまっていますが、「21 rows × 21 columns」となっており、縦横20の特徴量と1つのターゲットから構成されていることが分かります。
相関マップを表示
最後に相関マップを表示します。
こちらも前の記事同様に「seaborn」と「matplotlib」のインポート、グラフをjupyter notebook内で表示するためのマジックコマンドを記載し、グラフサイズの設定、seabornのヒートマップで相関図を作成します。

<セル4>
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline
plt.figure(figsize=(15,12))
sns.heatmap(corr, annot=True)
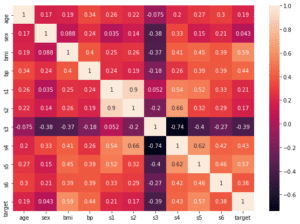
実行結果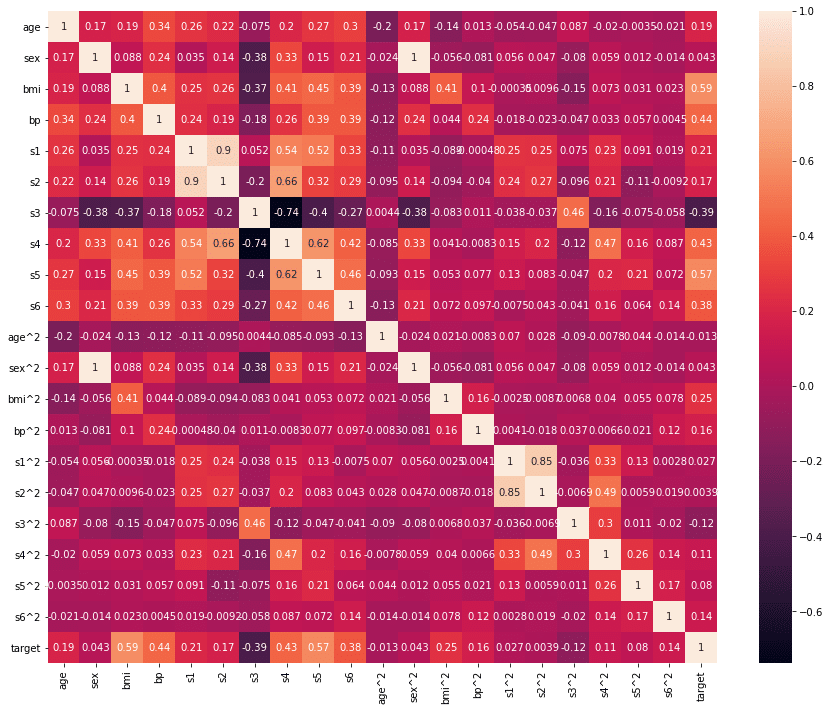
ということで表示できました。
注目すべきは一番右のtargetの列です。
上から10個はそのままの値で、bmiとs5の値が他よりも高くなっており、相関が高いことが分かります。
同じように下の10個(1番下のtargetの行を除く)の二乗した特徴量の値を見てみましょう。
すると軒並み低い値(絶対値として0に近い)になっていることが分かります。
つまり相関は低いということです。
残念ながら二乗では良い特徴量とはなりませんでしたし、同じように考えると三乗、四乗と数を増やしていっても、良い特徴量とはならなさそうです。
ただ一つ分かったのは、何らかの計算を行うことで、特徴量の質は変わるということです。
つまり計算を行うことには意味があり、良い特徴量とすることも可能かもしれません。
ということで次回はさらに特徴量同士を掛け合わせてみて、良い特徴量にならないか検討してみたいと思います。
ではでは今回はこんな感じで。

コメント